Собственные значения и собственные вектора матриц

Число 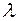называется собственным значением (или характеристическим числом) квадратной матрицы порядка , если можно подобрать такой –мерный ненулевой вектор 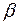, что .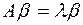

Для того, чтобы найти собственные значения матрицы , рассмотрим матрицу:

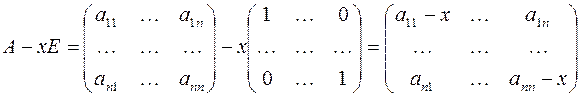
Если раскрыть определитель матрицы 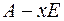, то получится многочлен –й степени:

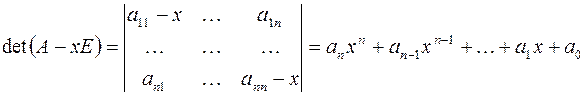
Этот многочлен называется характеристическим многочленом матрицы . Его коэффициенты 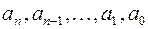зависят от элементов матрицы . Понятие многочлена будет подробно разобрано в следующем разделе.

Следует отметить, что 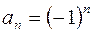, 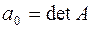. Уравнение 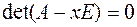называется характеристическим уравнением матрицы .

Теорема. Множество 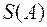всех собственных значений матрицы совпадает с множеством всех решений характеристического уравнения 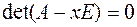матрицы .

Доказательство:

,

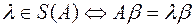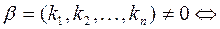
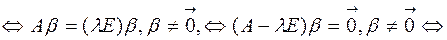
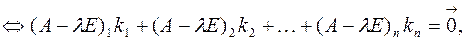
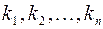–ненулевой набор чисел, 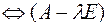– вырожденная матрица 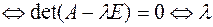– решение уравнения:

.

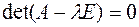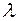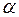Собственным вектором квадратной матрицы порядка , принадлежащим ее собственному значению называется -мерный вектор , для которого .

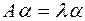Множество всех собственных векторов матрицы , принадлежащих ее собственному значению 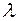, обозначим через 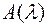. Отыскание собственных векторов сводится к решению однородной системы линейных уравнений.

Теорема. Множество 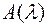всех собственных векторов матрицы порядка , принадлежащих ее собственному значению 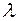, совпадает с множеством всех решений однородной системы линейных уравнений 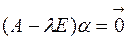, где .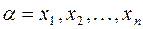

Доказательство:

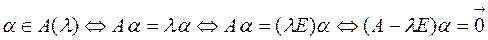
В развернутом виде равенство 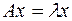записывается как система уравнений:

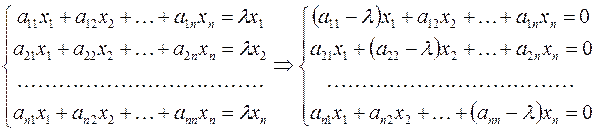
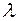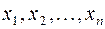Если зафиксировано число , то задача нахождения собственного вектора матрицы сводится к поиску ненулевого решения системы линейных однородных уравнений с неизвестными , которые являются координатами вектора 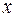. Эта система имеет ненулевое решение только тогда, когда выполняется условие:

,

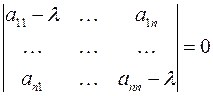т.е. число 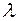является собственным числом матрицы .

Знание всех собственных векторов матрицы позволяет решить задачу диагонализации этой матрицы, то есть нахождения треугольной или диагональной матрицы, имеющий такие же собственные значения.

Теорема. Предположим, что квадратная матрица -го порядка имеет линейно независимых собственных векторов. Тогда если взять эти векторы в качестве столбцов матрицы 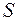, то матрица 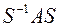будет диагональной матрицей, у которой на диагонали стоят собственные значения матрицы , т.е.:

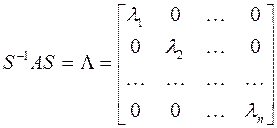
Теорема. Есл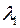и и 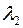– два различных собственных значения симметрической матрицы , то соответствующие им собственные векторы 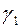и 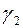удовлетворяют соотношению 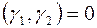, т.е. они ортогональны.

Таким образом, собственные значения симметрической матрицы различны, а, значит, если пронормировать соответствующие им собственные векторы, то система собственных векторов матрицы станет ортонормированной, а матрица 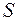, столбцами которой будут эти векторы, станет ортогональной.

Ортогональной называется вещественная квадратная матрица, у которой соответствующая ей система векторов-столбцов является ортонормированной системой евклидова пространства.

Теорема. Матрица является ортогональной тогда и только тогда, когда .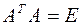

В соответствии с этой теоремой 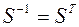, и преобразование 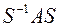эквивалентно преобразованию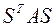

При определении характеристических чисел матрицы было введено новое понятие характеристического многочлена. Подробный анализ понятия многочлена приводится в следующем разделе.

Контрольные вопросы к лекции №10

1. Переход к новому базису и понятие матрицы перехода.

2. Понятие линейного оператора.

3. Собственные значения и собственные вектора матрицы.

4. Операция диагонализации матрицы и понятие ортогональной матрицы.

Лекция 11. Многочлены

Основные понятия:

Многочлен; степень многочлена; коэффициенты; старший коэффициент; сложение многочленов; умножение многочленов; делитель; частное; остаток; корень многочлена; кратность корня многочлена; линейные многочлены; схема Горнера; рациональная дробь; правильная рациональная дробь; простейшие (или элементарные) дроби; метод неопределенных коэффициентов.

Основные понятия

Многочленом от переменной 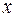степени называется выражение вида:

,

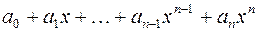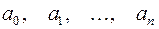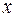где ‑ действительные или комплексные числа, называемые коэффициентами, ‑ натуральное число, ‑ переменная величина, принимающая произвольные числовые значения.

Если коэффициент 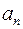при 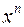многочлена 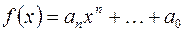отличен от нуля, а коэффициенты при более высоких степенях равны нулю, то число называется степенью многочлена, 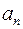– старшим коэффициентом, а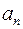 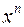– старшим членом многочлена. Коэффициент 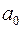называется свободным членом. Если все коэффициенты многочлена равны нулю, то многочлен называется нулевым и обозначается 0. Степень нулевого многочлена не определена.

Два многочлена называются равными, если они имеют одинаковую степень и коэффициенты при одинаковых степенях равны.

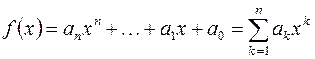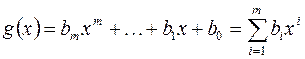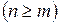Суммой многочленов и , называется многочлен 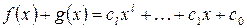, где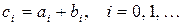

Произведением многочленов 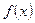и называется многочлен:

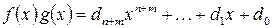
где .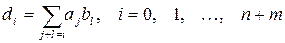

Легко проверить, что сложение и умножение многочленов ассоциативно, коммутативно и связаны между собой законом дистрибутивности.

Многочлен называется делителем многочлена , если существует многочлен 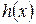такой, что .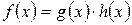