При выполнении деления комплексных чисел в тригонометрической форме их аргументы вычитаются, а модули нужно разделить.

Формула Муавра. Извлечение корня из комплексного числа

Используя формулу умножения комплексных чисел (3.3), получим формулу возведения комплексного числа в степень, называемую формулой Муавра:

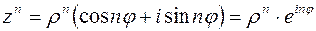(3.5)

Из нее следует, что для возведения комплексного числа в любую натуральную степень его модуль нужно возвести в эту степень, а аргумент умножить на показатель этой степени.

Перейдем к процедуре извлечения корней. Известно, что во множестве действительных чисел не из всякого действительного числа можно извлечь корень. Например, 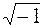не существует. В множестве комплексных чисел дело обстоит иначе.

Пусть 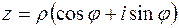. Комплексное число 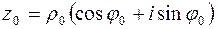называется корнем 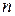-й степени из 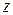, если 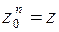, т.е.:

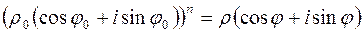
или

.

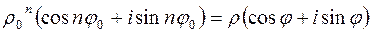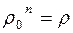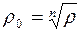Модуль комплексного числа определяется однозначно, поэтому или (здесь имеется в виду арифметический корень).

Аргумент комплексного числа определяется с точностью до 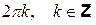. Следовательно, 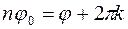, а .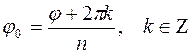

Таким образом, комплексное число 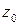, которое является корнем 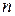-й степени из 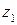имеет вид:

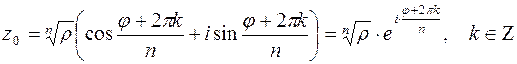(3.6)

Придавая 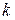различные значения, мы не всегда будем получать различные корни. Действительно, 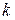можно записать в ви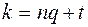де , где 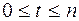. Тогда:

,

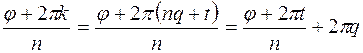Т.е. значение аргумента при данном 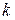отличается от значения аргумента при 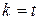на число, кратное 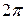. Следовательно, в формуле (2) можно ограничится лишь значениями 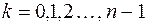. При таких значениях 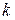получаются различные корни, так как разность между их аргументами по абсолютной величине меньше .

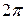Итак, для каждого ненулевого числа 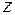существует ровно корней -й степени из .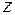

Пример. Вычислить .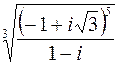

Представим число, стоящее под знаком корня, в тригонометрической форме:

.

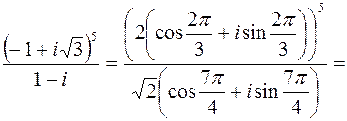
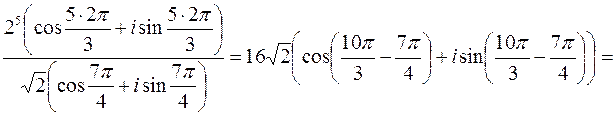
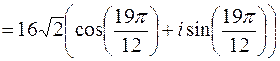Извлечем далее корень третьей степени из этого комплексного числа:

.

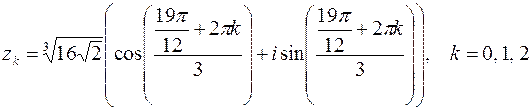Отсюда полагая, что 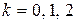, получим:

;

;

.

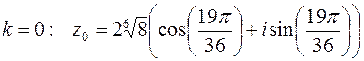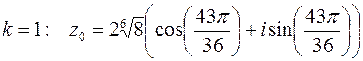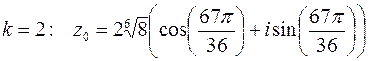Контрольные вопросы к лекции №3

1. Счетные и несчетные числовые множества.

2. Ограниченные множества.

3. Границы и грани множеств.

4. Соединения элементов.

5. Вычисление числа размещений, перестановок и сочетаний.

6. Понятие комплексного числа.

7. Понятие мнимой единицы (числа).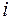

8. Основные операции над комплексными числами.

9. Представление комплексного числа в тригонометрической форме.

10. Понятие модуля комплексного числа.

11. Понятие аргумента комплексного числа.

12. Охарактеризовать умножение и деление комплексных чисел в тригонометрической форме.

13. Формула Муавра.

ТЕМА 2. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ

Лекция 4. Векторы

Основные понятия:

скалярная величина; векторная величина; коллинеарные векторы; компланарные векторы; единичный вектор; сложение векторов; проекция вектора; линейная комбинация векторов; линейная зависимость векторов; базис; координаты вектора; базисные орты; правая система координат; направляющие косинусы; скалярное произведение; векторное произведение; смешанное произведение.

Основные понятия

Понятие вектора широко применяется в экономике, математике, физике и других науках, при этом одинаково широко используется как алгебраическая концепция изложения векторного анализа, так и его геометрическая интерпретация, в рамках которой различаются величины двух видов: скалярные и векторные.

Скалярной величиной или скаляром называется величина, которая полностью определяется одним числом, выражающим отношение этой величины к соответствующей единице измерения, например, цена, количество проданного товара, стоимость и т.д.

Векторной величиной или вектором называется величина, для задания которой кроме численного значения необходимо указать и ее направление в пространстве, например, изменение темпов производства (рост или падение), колебание курса акций на бирже и т.д.

Векторная величина графически обычно изображается как связанный вектор или направленный отрезок, т.е. отрезок прямой, у которого указано, какая из ограничивающих точек является его началом, а какая концом. Но в отличие от направленного отрезка, для описания которого необходимо указать начальную точку, длину и направление, свободный вектор или просто вектор представляет собой множество всех эквивалентных между собой связанных векторов и вполне характеризуется:

· направлением;

· длиной (модулем).

Для задания такого множества достаточно указать какой-либо один из связанных векторов этого множества – представитель вектора, в качестве которого обычно выбирается связанный вектор с началом, совпадающим с началом координат.

Вектор обозначается одной маленькой буквой со стрелкой сверху, например, 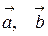, или двумя буквами со стрелкой 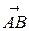, где точка есть начало вектора (его точка приложения), а 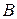‑ его конец.

Длина вектора называется его модулем, обозначается 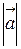или 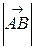и равна длине любого его представителя, т.е. расстоянию между начальной и конечной точками связного вектора 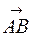. Вектор, длина которого равна нулю, называется нуль-вектором и обозначается .

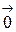Два вектора называются равными, если:

1. равны их длины;

2. они параллельны;

3. они направлены в одну сторону.

Иными словами, равные векторы получаются один из другого параллельным переносом в пространстве.

Векторы называются коллинеарными, если они расположены на одной или на параллельных прямых, и компланарными, если они лежат на одной или на параллельных плоскостях.

Вектор, длина которого равна единице, называется единичным векторомили ортом. Орт обозначатся 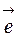.