Основные операции над множествами
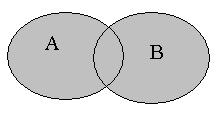 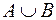 Рис. 2.2. Рис. 2.2. | Суммой или объединением двух или произвольного (даже бесконечного) числа заданных множеств называется множество, состоящее из всех элементов, принадлежащих хотя бы одному из заданных множеств. Эта операция над множествами обозначается знаком 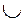 . . |
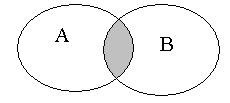 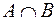 Рис. 2.3. Рис. 2.3. | Произведением или пересечением двух или произвольного (даже бесконечного) числа заданных множеств называется множество, состоящее из всех элементов, принадлежащих каждому из заданных множеств. Эта операция над множествами обозначается знаком 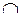 . Если . Если 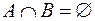 , то множества , то множества  и и 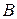 называются непересекающимися. называются непересекающимися. |
Два множества называются непересекающимися (или расчлененными) если 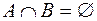 . Практический интерес представляют разбиения множества на взаимно непересекающиеся подмножества (эту задачу иногда называются классификацией). Разбиением множества
. Практический интерес представляют разбиения множества на взаимно непересекающиеся подмножества (эту задачу иногда называются классификацией). Разбиением множества  называется такая расчлененная система непустых подмножеств множества
называется такая расчлененная система непустых подмножеств множества  , что каждый элемент множества
, что каждый элемент множества  является элементом некоторого единственного множества этой системы. Возможность разбиения множества на непересекающиеся подмножества зависит от признака, по которому производится разбиение.
является элементом некоторого единственного множества этой системы. Возможность разбиения множества на непересекающиеся подмножества зависит от признака, по которому производится разбиение.
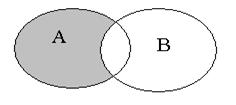 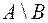 Рис. 2.4. Рис. 2.4. | Разностью множеств  и и 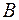 или дополнением или дополнением 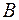 до до  называется множество, состоящее только из тех элементов называется множество, состоящее только из тех элементов  , которые не входят в , которые не входят в 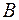 . Эта операция над множествами обозначается знаком . Эта операция над множествами обозначается знаком 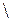 . . |
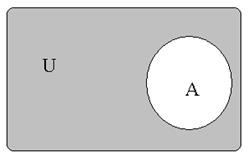 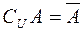 Рис. 2.5. Рис. 2.5. | Часто все рассматриваемые множества считают подмножествами одного основного множества 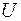 . В таком случае разность . В таком случае разность 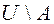 (дополнение (дополнение  до до 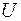 ) обозначают, как ) обозначают, как 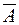 , а операцию называют взятием дополнения. , а операцию называют взятием дополнения. |
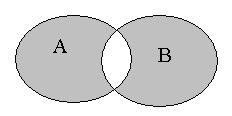 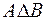 Рис. 2.6. Рис. 2.6. | Симметрической разностью множеств  и и 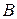 называется множество называется множество 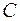 : : 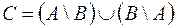 . Обозначается симметрическая разность: . Обозначается симметрическая разность: 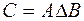 или или 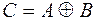 . . |
Для подмножеств данного множества 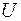 выполняются следующие законы:
выполняются следующие законы:
· Закон коммутативности (переместительный закон):
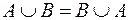 ;
; 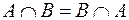 ;
;
· Закон ассоциативности (сочетательный закон) для любой тройки множеств  ,
, 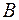 и
и 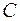 :
:
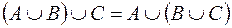 ;
;
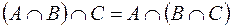 ;
;
· Закон дистрибутивности (распределительный закон) для любой тройки множеств 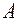 ,
, 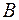 и
и 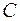 :
:
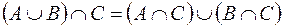 ;
;
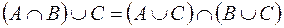 ;
;
· 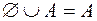 ;
; 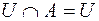 ;
;
· 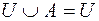 ;
; 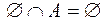 ;
;
· 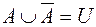 ;
; 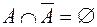 ;
;
· 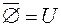 ;
;
· 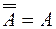 ;
;
· 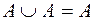 ;
; 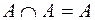 ;
;
· 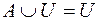 ;
; 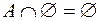 ;
;
· 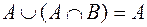 ;
; 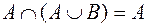 ;
;
· 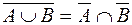 ;
; 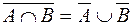 .
.
Если операции объединения множеств поставить в соответствие операцию сложения чисел, операции пересечения множеств – операцию умножения, универсальному множеству 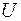 – единицу, а пустому множеству – ноль, то возникает аналогия между множествами и числами. Операции объединения и пересечения множеств, как и действия над действительными числами, подчиняются законам коммутативности, ассоциативности и дистрибутивности. Можно также провести аналогию между свойствами логических операций, где логической эквивалентности соответствует операция равенства, а операциям конъюнкции и дизъюнкции – операции объединения и пересечения.
– единицу, а пустому множеству – ноль, то возникает аналогия между множествами и числами. Операции объединения и пересечения множеств, как и действия над действительными числами, подчиняются законам коммутативности, ассоциативности и дистрибутивности. Можно также провести аналогию между свойствами логических операций, где логической эквивалентности соответствует операция равенства, а операциям конъюнкции и дизъюнкции – операции объединения и пересечения.
Свойства фигурируют попарно таким образом, что каждое получается из соседнего заменой 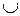 на
на 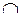 ,
, 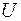 на
на 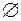 и наоборот. Такие выражения называются двойственными друг другу.
и наоборот. Такие выражения называются двойственными друг другу.
Принцип двойственности. Для любого тождества множеств двойственное ему выражение также является тождеством.
Очевидно, что операция разность не обладает свойствами коммутативности и ассоциативности, в то же время операция симметрическая разность и коммутативна, и ассоциативна.
Большое значение в современной математике имеет множественная операциядекартово произведение.Если заданы два множества  и
и 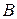 , то из их элементов можно составить упорядоченные пары, взяв сначала какой-либо элемент первого множества, а затем – элемент второго множества. Декартовым произведением двух исходных множеств
, то из их элементов можно составить упорядоченные пары, взяв сначала какой-либо элемент первого множества, а затем – элемент второго множества. Декартовым произведением двух исходных множеств  и
и 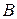 называется множество
называется множество 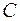 , составленное из упорядоченных пар (
, составленное из упорядоченных пар ( 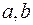 ). Декартово произведение множеств
). Декартово произведение множеств  и
и 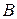 обозначается
обозначается 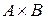 .
.
Очевидно, что 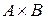 и
и 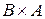 ‑ различные множества, т.е. операция декартова произведения не коммутативна, но, в то же время, она обладает свойством ассоциативности.
‑ различные множества, т.е. операция декартова произведения не коммутативна, но, в то же время, она обладает свойством ассоциативности.
Отображения
Отображение – одно из основных понятий математики. Отображение есть какое-либо правило или закон соответствия множеств. Пусть  и
и 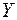 – произвольные непустые множества. Говорят, что задано отображение
– произвольные непустые множества. Говорят, что задано отображение 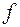 множества
множества  на множество
на множество 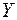 (запись:
(запись: 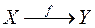 или
или 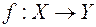 ) если каждому элементу
) если каждому элементу 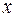 множества
множества  (
( 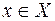 ) поставлен соответствие единственный, однозначно определенный элемент
) поставлен соответствие единственный, однозначно определенный элемент 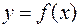 множества
множества 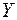 (
( 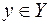 ).
).
Элемент 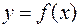 называется образом элемента
называется образом элемента 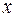 при отображении
при отображении 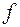 , а элемент
, а элемент 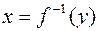 называется прообразом элемента
называется прообразом элемента 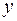 при этом отображении. Образом множества
при этом отображении. Образом множества  элементов
элементов 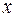 при отображении
при отображении 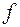 называется множество всех элементов вида
называется множество всех элементов вида 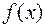 , принадлежащих области значений
, принадлежащих области значений 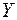 . Множество
. Множество  всех элементов
всех элементов 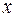 (
( 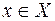 ), образы которых
), образы которых 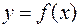 составляютобласть значений
составляютобласть значений 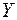 называется прообразом множества
называется прообразом множества 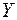 элементов
элементов 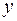 (
( 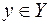 ). Множество
). Множество  называется областью определения отображения
называется областью определения отображения 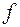 .
.
Отображение 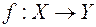 называется сюръективным, когда каждый элемент
называется сюръективным, когда каждый элемент 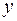 множества
множества 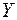 (
( 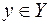 ) имеет хотя бы один прообраз
) имеет хотя бы один прообраз 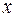 множества
множества  (
( 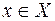 ), т.е.
), т.е. 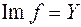 , или
, или 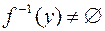 .
.
Отображение 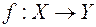 называется инъективным, когда каждый элемент
называется инъективным, когда каждый элемент 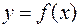 множества
множества 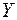 (
( 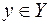 )является образом лишь одного элемента
)является образом лишь одного элемента 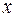 множества
множества  (
( 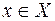 ), т.е. образы любых двух различных элементов множества
), т.е. образы любых двух различных элементов множества  различны, т.е. из
различны, т.е. из 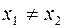 следует
следует 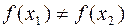 .
.
Отображение 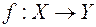 называется биективнымили взаимно однозначным, когда оно одновременно инъективно и сюръективно, т.е. каждый элемент множества
называется биективнымили взаимно однозначным, когда оно одновременно инъективно и сюръективно, т.е. каждый элемент множества 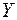 является образом одного и только одного элемента множества
является образом одного и только одного элемента множества  .
.
Равенство двух отображений 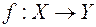 и
и 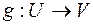 означает по определению, что их соответствующие области совпадают (
означает по определению, что их соответствующие области совпадают ( 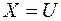 и
и 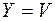 ), причем
), причем 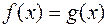
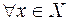 .
.
Произведение двух отображений 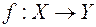 и
и 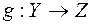 можно определить как отображение
можно определить как отображение 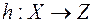 , которое каждому элементу
, которое каждому элементу 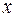 множества
множества 
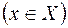 ставит в соответствие элемент
ставит в соответствие элемент 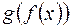 множества
множества 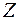
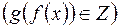 .
.
Отображение 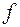 множества
множества  на множество
на множество 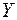 иначе называется функцией на множестве
иначе называется функцией на множестве  со значениями во множестве
со значениями во множестве 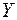 . Если множества
. Если множества  и
и 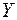 совпадают, то биективное отображение множества
совпадают, то биективное отображение множества  на себя
на себя 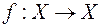 называется преобразованием множества
называется преобразованием множества  . Простейшее преобразование множества
. Простейшее преобразование множества  – тождественное
– тождественное 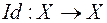 – определяется так:
– определяется так: 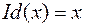
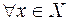 . Тождественное отображение
. Тождественное отображение 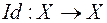 , переводящее каждый элемент
, переводящее каждый элемент 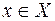 в себя, также называют единичным преобразованием. Если заданы преобразования
в себя, также называют единичным преобразованием. Если заданы преобразования 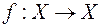 и
и 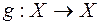 , то преобразование
, то преобразование 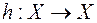 , являющееся результатом последовательного выполнения сначала преобразования
, являющееся результатом последовательного выполнения сначала преобразования 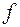 , а затем и преобразования
, а затем и преобразования 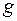 , называется произведением преобразований
, называется произведением преобразований 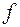 и
и 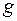 :
: 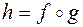 .
.
Для преобразований 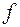 ,
, 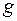 и
и 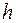 одного и того же множества
одного и того же множества  справедливы следующие законы:
справедливы следующие законы:
· 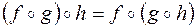
· 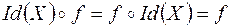
· 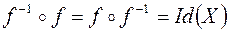
Коммутативный закон для произведения преобразований в общем случае не выполняется, т.е. 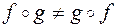 .
.
Если между двумя множествами можно задать биективное отображение (установить взаимно однозначное соответствие между их элементами), то такие множества называются эквивалентными или равномощными. Конечные множества равномощны только в том случае, когда число их элементов одинаково.
Бесконечные множества также можно сравнивать между собой.
Два множества имеют одинаковую мощность или называются эквивалентными (обозначение 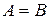 ), если между их элементами можно установить взаимно однозначное соответствие, т.е. если можно указать некоторое правило, в соответствии с которым каждому элементу одного из множеств соотносится один и только один элемент другого множества.
), если между их элементами можно установить взаимно однозначное соответствие, т.е. если можно указать некоторое правило, в соответствии с которым каждому элементу одного из множеств соотносится один и только один элемент другого множества.
Если же подобное отображение невозможно, то множества имеют различную мощность; при этом оказывается, что в последнем случае, каким бы образом мы не пытались привести в соответствие элементы обоих множеств, всегда останутся лишние элементы и притом всегда от одного и того же множества, которому приписывается более высокое значение кардинального числа или говорят, что это множество имеет бόльшую мощность.
Бесконечное множество и некоторое его подмножество могут быть эквивалентными.
Множество, эквивалентное множеству натуральных чисел, называется счетным множеством. Для того чтобы множество  было счетным, необходимо и достаточно, чтобы каждому элементу
было счетным, необходимо и достаточно, чтобы каждому элементу 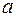 множества
множества  был поставлен в соответствие его порядковый номер
был поставлен в соответствие его порядковый номер 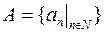 . Из всякого бесконечного множества можно выделить счетное подмножество. Всякое подмножество счетного множества является счетным или конечным. Счетное множество является наиболее примитивно организованным бесконечным множеством. Декартово произведение двух счетных множеств является счетным. Объединение конечного или бесконечного числа конечных или счетных множеств является конечным или счетным множеством.
. Из всякого бесконечного множества можно выделить счетное подмножество. Всякое подмножество счетного множества является счетным или конечным. Счетное множество является наиболее примитивно организованным бесконечным множеством. Декартово произведение двух счетных множеств является счетным. Объединение конечного или бесконечного числа конечных или счетных множеств является конечным или счетным множеством.
