Операции над множествами
Объединение двух множеств А и В – это новое множество, элементами которого являются элементы, принадлежащие множеству А или множеству В. Обозначение: А 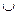 В.
В.
А 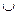 В={x| х
В={x| х 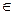 А или х
А или х 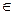 В}.
В}.
Пересечение двух множеств А и В – это новое множество, элементами которого являются элементы, принадлежащие множеству А и множеству В. Обозначение: А 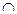 В.
В.
А 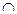 В={x| х
В={x| х 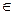 А и х
А и х 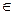 В}.
В}.
Разность двух множеств А и В – это новое множество, элементами которого являются элементы, принадлежащие множеству А и не принадлежащие множеству В. Обозначение: А \ В.
А \ В={x| х 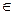 А и х
А и х 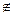 В}.
В}.
Обычно элементы множеств выбираются из некоторого достаточно широкого множества U, которое называется универсум. В связи с этим понятием можно ввести операцию дополнение.
Дополнением множества А называется множество, которое состоит из элементов универсума, не принадлежащих множеству А. Обозначение: 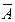 .
.
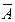 =U \ A или
=U \ A или 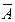 ={x| х
={x| х 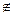 А и х
А и х 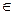 U}.
U}.
Пример: U={1, 2, 3, 4, 5, 6, 7}, A={1, 2, 3, 4, 5}, В={2, 4, 6}.
А 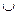 В = {1, 2, 3, 4, 5, 6} А
В = {1, 2, 3, 4, 5, 6} А 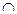 В = {2, 4} А \ В = {1, 3, 5}
В = {2, 4} А \ В = {1, 3, 5}
В \ А = {6} 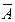 = {6, 7}
= {6, 7} 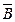 = {1, 3, 5, 7}
= {1, 3, 5, 7}
Для наглядного изображения соотношений между множествами и изображения результатов операций над множествами используют диаграммы Эйлера.
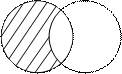
 Пример:
Пример:
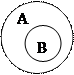 |  | ||
B 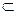 A А
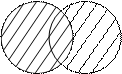
A А 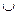 В А
В А 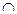 В А \ В
В А \ В
Свойства операций над множествами.
Идемпотентность пересечения, объединения.
А 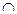 А = А А
А = А А 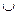 А = А
А = А
Коммутативность пересечения, объединения.
А 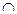 В = В
В = В 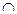 А А
А А 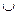 В = В
В = В 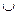 А
А
Ассоциативность пересечения, объединения.
(А 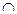 В)
В) 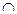 С = А
С = А 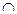 (В
(В 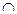 С) (А
С) (А 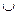 В)
В) 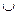 С = А
С = А 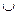 (В
(В 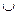 С)
С)
Законы поглощения.
(А 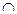 В)
В) 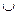 А = А (А
А = А (А 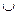 В)
В) 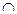 A = А
A = А
Свойства пустого множества.
А 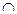
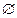 =
= 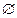 А
А 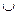
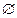 = А
= А
Свойства универсума.
А 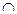 U = A А
U = A А 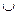 U = U
U = U
Инволютивность.
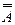 = А
= А
Законы де Моргана.
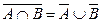
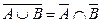
Свойства дополнения.
А 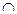
 =
= 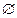 А
А 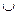
 = U
= U
Выражения для разности.
А \ В = А 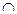
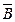
Основы математической логики
Логические представления – описание исследуемой системы, процесса, явления в виде совокупности сложных высказываний, составленных из простых (элементарных) высказываний и логических связок между ними. Логические представления и их составляющие характеризуются определенными свойствами и набором допустимых преобразований над ними (операций, правил вывода и т.п.), реализующих разработанные в формальной (математической) логике правильные методы рассуждений – законы логики
Логика высказываний
Способы (правила) формального представления высказываний, построения новых высказываний из имеющихся с помощью логически выдержанных преобразований, а также способы (методы) установления истинности или ложности высказываний изучаются в математической логике. Современная математическая логика включает два основных раздела: логику высказываний и охватывающую ее логику предикатов, для построения которых существуют два подхода (языка), образующих два варианта формальной логики: алгебру логики и логические исчисления. Между основными понятиями этих языков формальной логики имеет место взаимно однозначное соответствие.
Основными объектами традиционных разделов логики являются высказывания.
Высказывание – повествовательное предложение (утверждение, суждение), о котором имеет смысл говорить, что оно истинно или ложно. Все научные знания (законы и явления физики, химии, биологии и др., математические теоремы и т.п.), события повседневной жизни, ситуации формализуются в виде высказываний. Повелительные, вопросительные и бессмысленные предложения не являются высказываниями.
Примеры высказываний: дважды два – четыре, мы живем в 21 веке.
Для того чтобы далее оперировать этими предложениями как высказываниями, мы обязаны знать относительно каждого из них, истинно оно или ложно, т.е. знать их истинное значение (истинность).
Основные понятия логики высказываний
В формально-логических выводах используются истинные и ложные предложения.
Определение: повествовательное предложение, о котором можно однозначно сказать, истинно оно или ложно, называется высказыванием.
Примеры высказываний: "кит - животное", "все углы - прямые" и т. п. Первое из этих высказываний является, очевидно, истинным, а второе - ложным. Предложение "реши задачу", также как и "2+2", не является высказываем.
Определения математических понятий не являются высказываниями, т.к. это принятые соглашения.
Будем обозначать высказывания большими латинскими буквами: A, B, C,….
Элементарные, нерасчленяемые высказывания будем называть атомами. Употребляемые в обычной речи логические связки "и", "или", "если..., то...", "эквивалентно", частица "не" и т. д. позволяют из уже заданных высказываний строить новые, более "сложные" высказывания.
Аналогично тому, как в языке из простых предложений с помощью логических связок образуются сложные предложения, так и в логике высказываний из атомов можно образовывать составные высказывания.
Истинность или ложность получаемых таким образом высказываний зависит от истинности и ложности исходных высказываний и соответствующей трактовки связок как операций над высказываниями.
Рассмотрим определения логических операций, соответствующих логическим связкам.
Каждому высказывания можно сопоставить его истинностное значение, обозначаемое соответственно через И (если высказывание истинно), Л (если высказывание ложно).
Истинностное значение сложных высказываний зависит от истинностных значений высказываний, составлявших слоеное высказывание.
Эта зависимость устанавливается в данных ниже определениях я стращается в таблицах истинности.
