Операции над событиями. Условная вероятность. Теоремы сложения и умножения вероятностей.
3.3.1.Игральная кость подбрасывается один раз. Наблюдаемый результат – выпавшее число очков. Рассмотрим события: А1 – выпавшее число кратно трем; А2 – выпавшее число нечетно; А3 – выпавшее число не меньше трех; А4 – выпавшее число не больше двух; А5 – выпало число от 2 до 4. Выяснить, какие из этих событий являются попарно несовместными. Сформулировать, в чем состоят события 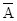 2,,
2,, 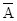 3, А1А2, А1+А2, А1А3, А1+А3, А1А4, А1+А4, А1А5, А2А3, А2А5, А2+А5, А3А4, А3+А4, А3А5, А3+А5, А4+А5, А1+А2+А5.
3, А1А2, А1+А2, А1А3, А1+А3, А1А4, А1+А4, А1А5, А2А3, А2А5, А2+А5, А3А4, А3+А4, А3А5, А3+А5, А4+А5, А1+А2+А5.
3.3.2.Из партии калькуляторов выбирают пять калькуляторов для проверки. Наблюдаемый результат – число калькуляторов, имеющих брак. Рассмотрим события: А1 – число бракованных калькуляторов не более трех; А2 – бракованных калькуляторов – три; А3 – число бракованных калькуляторов не менее двух; А4 – есть хотя бы четыре калькулятора с браком; А5 – есть хотя бы один калькулятор с браком. Выяснить, какие из этих событий являются попарно несовместными. Сформулировать, в чем состоят события 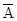 1,
1, 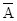 2,
2, 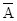 4,
4, 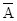 5, А1А3, А1+А3, А2А3, А2+А3, А1А5, А1+А5, А2+А4, А2А5, А3А4, А3+А4.
5, А1А3, А1+А3, А2А3, А2+А3, А1А5, А1+А5, А2+А4, А2А5, А3А4, А3+А4.
3.3.3. Производится осмотр телевизора, при котором можно обнаружить всего 4 различных дефекта. Наблюдаемый результат – количество обнаруженных дефектов. Рассмотрим события: А1 – обнаружен один дефект; А2 – обнаружено два дефекта; А3 – обнаружено три дефекта; А4 – обнаружены все дефекты; А5 – обнаружен хотя бы один дефект; А6 – обнаружено не менее двух дефектов; А7 – обнаружено не более двух дефектов. Выяснить, какие события являются попарно несовместными. Сформулировать, в чем состоят события 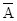 4,
4, 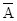 5,
5,  7, А1А5, А1+А5, А1А6, А1+А6, А1А7, А1+А7, А3А4, А3+А4, А5А7, А5+А7, А6А7, А6+А7, А2+А3+А4.
7, А1А5, А1+А5, А1А6, А1+А6, А1А7, А1+А7, А3А4, А3+А4, А5А7, А5+А7, А6А7, А6+А7, А2+А3+А4.
3.3.4. Электрическая цепь составлена по схеме, приведенной на рис.1. Событие Аk – элемент с номером k вышел из строя, k=1,2,3,4; событие В – разрыв цепи. Выразить событие В в алгебре событий А1, А2, А3, А4.
 |





 2
2





 1 4
1 4
3 
 Рис.1
Рис.1
3.3.5. Электрическая цепь составлена по схеме, приведенной на рис.2. Событие Аk – элемент с номером k вышел из строя, k=1,2,3,4,5; событие В – разрыв цепи. Выразить событие В в алгебре событий А1, А2, А3, А4, А5.






 1 2
1 2
 |


 3
3
 |  |


 4 5 Рис.2
4 5 Рис.2
3.3.6. Из урны, в которой находятся 7 черных и 8 белых шаров, вынимают наугад три шара. Найти вероятность того, что они будут одного цвета.
3.3.7.Из колоды в 36 карт вынимают 7 карт. Найти вероятность того, что среди них 4 дамы или 4 короля.
3.3.8.Среди пяти одинаковых пар обуви наугад выбирают 4 башмака. Найти вероятность того, что хотя бы два из них составят пару.
3.3.9. Один раз подбрасывается игральная кость. События: А – выпало простое число очков; В – выпало четное число очков. Вычислить вероятности Р (А) и Р (А/В).
3.3.10. Два раза подбрасывается игральная кость. События: А – оба раза выпало число очков, кратное 3; В – оба раза выпало одно и то же число очков. Вычислить вероятности Р (А) и Р (А/В).
3.3.11. Из колоды в 36 карт вынимают две карты. Найти вероятность того, что: а) это тузы; б) это тузы при условии, что вынуты красные карты.
3.3.12. Из колоды в 36 карт вынимают 4 карты. Найти вероятность того, что: а) это дамы; б) это дамы при условии, что все вынутые карты – разных мастей.
3.3.13. Заключение сделки состоит из двух последовательных независимых этапов. Вероятность успешного прохождения первого этапа равна 0,9, второго этапа – 0,8. Найти вероятность того, что сделка будет заключена.
3.3.14.Коммерсант договаривается о поставке товаров с двумя поставщиками, действующими независимо друг от друга. Вероятность того, что первый поставщик поставит товар, равна 0,95, а того, что второй – 0,6. Найти вероятность того, что коммерсант получит товар (т.е. товар поставит хотя бы один поставщик).
3.3.15. В магазине установлены две независимо работающие системы сигнализации. Вероятность несрабатывания первой системы равна 0,05, второй системы – 0,02. Найти вероятность того, что в случае необходимости сработает хотя бы одна система сигнализации.
3.3.16. Для охраны банка созданы три независимо работающие системы безопасности, вероятности отказа которых равны соответственно 0,05, 0,02 и 0,01. Какова вероятность того, что в случае несанкционированного проникновения в банк сработает хотя бы одна система безопасности?
3.3.17. Прибор состоит из четырех последовательно соединенных блоков. Надежность каждого блока (т.е. вероятность безотказной работы в течение установленного времени Т) равна 0,9, причем отказы блоков являются независимыми в совокупности событиями. Найти вероятность безотказной работы прибора в течение времени Т.
3.3.18. Найти надежность электрической схемы, приведенной на рис.3, если надежность любого из трех параллельно соединенных элементов этой схемы равна 0,8. Предполагается, что отказы элементов являются независимыми в совокупности событиями. Отказ любого из элементов приводит к прерыванию сигнала в той ветви цепи, где находится данный элемент.




 1
1
 |

 2
2




 3 Рис.3
3 Рис.3
3.3.19. Первый стрелок поражает мишень с вероятностью 0,6, второй – с вероятностью 0,5, третий – с вероятностью 0,3. Выстрелили все трое. Найти вероятность того, что мишень поражена.
3.3.20. Имеется деформированная монета, у которой вероятность выпадения решки равна 0,4, а орла – 0,6. Найти вероятность того, что при двукратном подбрасывании монеты она оба раза упадет на одну и ту же сторону.
3.3.21. В урне 4 белых и 6 черных шаров. Их вынимают по одному до появления первого белого шара. Найти вероятность того, что процесс оборвется: а) на втором шаре; б) на 3-ем шаре.
3.3.22. Студент, который знает 10 из 15 вопросов по первому разделу и 16 из 20 вопросов по второму разделу, получает по одному случайно выбранному вопросу из каждого раздела. Найти вероятность того, что студент ответит: а) правильно на оба вопроса; б) правильно на первый вопрос и неправильно на второй; в) правильно хотя бы на один вопрос; г) правильно на один вопрос.
3.3.23. Из хорошо перемешанной колоды в 36 карт вынимаются одна за другой две карты. Найти вероятность того, что среди вынутых карт: а) первая – дама, вторая – туз; б) обе – крестовой масти, причем первая – дама; в) обе – крестовой масти; г) одна дама и один туз; д) одна дама.
3.3.24. В магазин поступила большая партия товара: 40% партии – товар 1 сорта, 50% - товар 2 сорта, остальное – высшего качества. Найти вероятность того, что две случайным образом выбранные единицы товара – одного сорта.
3.3.25. В среднем 40 % урожая – яблоки 1-го сорта. Вероятность того, что товаровед примет первосортную партию 1-ым сортом, равна 0,85. Кроме того, он может допустить ошибку, считая непервосортную партию первосортной. Это происходит с вероятностью 0,25. Найти вероятность того, что товаровед неправильно установит сорт партии яблок.
3.3.26. В ящике 20 шаров, среди которых 4 белых. Шары выбираются наугад, пока не попадется белый. Найти вероятность следующего события A: будет выбрано ровно три шара.
3.3.27. Вероятность попадания в цель первым стрелком равна 2/3, вторым – 1/2. Первый стрелок сделал 2 выстрела, а второй – 3. Найти вероятность следующего события A: цель не поражена.
3.3.28. Инспектор проверяет состояние двух автомобилей. Вероятность полной исправности любого из автомобилей равна 0,9. Найти вероятность следующего события A: среди проверенных автомобилей ровно один полностью исправен.
3.3.29. Три стрелка одновременно выстрелили в цель. Вероятности попадания первого, второго и третьего стрелков соответственно равны 0,3; 0,6; 0,8. Найти вероятности следующих событий: A – цель поражена; B – в цель попал ровно один стрелок; C – в цель попали ровно два стрелка; D – в цель попали все стрелки; E – хотя бы один стрелок промахнулся.
3.3.30. В первом ящике 5 белых, 7 черных и 3 красных шара; во втором ящике 4 белых, 2 черных и 4 красных шара. Из каждого ящика наугад вынимается по одному шару. Найти вероятность следующего события A: оба выбранных шара – одного цвета.
