Математические модели угрозы атаки.

2.1. Обоснование возможности использования марковских моделей.

Информационную систему, как в отношении угрозы возникновения уязвимости, так и в отношении угрозы атаки в целом, создаваемой некой совокупностью уязвимостей, можно рассматривать, как систему с отказами и восстановлениями характеристики информационной безопасности (угрозу атаки, ввиду того, что при устранении уязвимости исчезает и реальная угроза атаки, предполагающей использование соответствующей уязвимости).

В теории надежности для моделирования систем с отказами и восстановлениями объектов (характеристики надежности), как правило, используется аппарат так называемых марковских случайных процессов при допущениях о пуассоновском характере потока заявок и о показательном распределении времени обслуживания. Как известно, процесс, протекающий в физической системе, называется марковским (или процессом без последействия), если для каждого момента времени вероятность любого состояния системы в будущем зависит только от состояния системы в настоящий момент и не зависит от того, каким образом система пришла в это состояние. Рассмотрим, может ли (корректно ли и в каких предположениях) использоваться данный аппарат в нашем случае - для моделирования систем с отказами и восстановлениями характеристики информационной безопасности. Это принципиальный вопрос. С этой целью рассмотрим, что собою представляет уязвимость, возникновение которых в системе создает реальную угрозу атаки.

Возникновение уязвимости в информационной системе в общем случае может быть вызвана двумя причинами - отсутствие, либо некорректность решения соответствующей задачи защиты (например, задача защиты от вредоносных программ может решаться запретом исполнения создаваемых интерактивными пользователями файлов [///], что не реализуется современными операционными системами), либо ошибки реализации средств информационной системы, например, ошибки программирования, которые могут эксплуатироваться нарушителем для обхода реализованной в системе защиты. Как ранее отмечали, в качестве эксплуатационных параметров уязвимости (типа уязвимостей) следует рассматривать интенсивность возникновения уязвимости 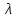, и интенсивность устранения уязвимости,µ. Под возникновением уязвимости естественно полагаем ее выявление нарушителем.

С одной стороны, предполагая, что система содержит конечное (пусть и очень большое) количество не выявленных уязвимостей, можем заключить, что в данном случае процесс не является марковским, поскольку выявление и устранение каждой уязвимости приводит к уменьшению их числа на конечном исходном множестве, т.е. имеем процесс с последействием, при этом входной поток не будет являться пуассоновским, поскольку в этих предположениях

Однако задумаемся над тем, как будут изменяться параметры уязвимости в процессе эксплуатации информационной системы на практике. Очевидно, что в общем случае интенсивность возникновения уязвимости (типа уязвимостей) 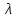по прошествии некоторого времени будет снижаться, поскольку в первую очередь нарушителем будут выявляться наиболее простые ошибки и недочеты реализации защиты (увеличение сложности выявления уязвимости естественно приведет к снижению интенсивности 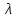). В отношении параметраµ можем сказать, что он никак не связан со сложностью выявления уязвимости, определяется исключительно типом уязвимости (например, ошибки в системных драйверах и в приложениях требуют различной трудоемкости исправления), т.е. для каждого типа уязвимости можем принять:

Теперь обратимся к задаче задания значений параметров уязвимости при проектировании системы защиты. Сразу оговоримся, что выявление при прогнозировании изменения этих параметров какого-либо тренда [///] серьезно ограничивается малым временем эксплуатации современных средств (в частности, программных, как правило, в течение нескольких лет выходит новая версия программного продукта). Естественно, что о прогнозной экстраполяции речь можно вести лишь при условии достаточности накопленной статистики, в нашем случае, при условии оценки параметров уязвимостей (соответствующих групп уязвимостей) за достаточно продолжительное время, по крайней мере, за несколько лет. Поэтому на практике более применима формальная экстраполяция [///].

Теперь допустим, мы спроектировали систему защиты, применив формальную экстраполяцию с использованием марковской модели. Тем самым при моделировании мы предположили, что поток без последействия, т.е. интенсивности возникновения уязвимости 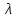, и устранения уязвимостиµ (соответствующих групп уязвимостей) будут неизменными в процессе последующей эксплуатации защищенной информационной системы. Очевидно, что с учетом сказанного ранее (а именно, что значение 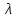будет только уменьшаться, а µ останется неизменным в процессе последующей эксплуатации системы), используя подобную модель мы найдем граничные (при худших для системы условиях) значения требуемых характеристик, учет которых гарантирует, что "хуже не будет". На самом же деле, определения значений именно таких характеристик нам и требуется (не можем же мы проектировать систему защиты, оперируя заниженными - с учетом их уменьшения в процессе эксплуатации системы, значениями параметров уязвимости). Вот если бы последействие приводило к увеличению 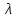в процессе эксплуатации информационной системы, тогда, другое дело, подобное последействие при моделировании необходимо было бы учитывать.

Из сказанного можем сделать вывод о том, что при моделировании угрозы атаки на информационную систему могут использоваться марковские модели, которые позволяют в данном случае определять требуемые граничные значения характеристик, которые и должны использоваться при проектировании систем защиты. Это существенно упрощает задачу моделирования угрозы атаки.

2.2. Модель реальной угрозы атаки.

Построим марковскую модель, описывающую возникновение реальной угрозы атаки в информационной системе при условии, что в системе создаются угрозы атаки, которые не используются нарушителем (рассматриваем систему с отказами и восстановлениями в отношении угрозы атаки, в отношении угрозы уязвимости система всегда должна рассматриваться, как система с отказами и восстановлениями).

Рассмотрим математическое описание марковского процесса с дискретными состояниями и непрерывным временем на примере орграфа угрозы атаки, см. рис.1, содержащего две взвешенные вершины уязвимостей (групп уязвимостей) - угроза атаки создается двумя уязвимостями, с соответствующими их параметрами – интенсивностями выявления и устранения уязвимостей. Граф системы состояний случайного процесса представлен на рис.2. На графе представлены четыре возможных состояния: – исходное состояние системы, в системе выявлена и не устранена первая уязвимость, – в системе выявлена и не устранена вторая уязвимость, – в системе выявлены и не устранены обе уязвимости.Будем полагать, что все переходы системы из одного состояния в другое происходят под воздействием простейших потоков событий с соответствующими интенсивностями выявления 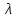или устраненияµ уязвимостей.

Рис.2. Граф системы состояний случайного процесса

Cистема дифференциальных уравнений Колмогорова для вероятностей состояний для данного графа будет иметь следующий вид:

Заменяя в уравнениях Колмогорова их производные нулевыми значениями, получим систему линейных алгебраических уравнений, описывающих стационарный режим:

Решая данную систему уравнений, с учетом полной группы событий, т.е., используя условие:

находим предельные (или финальные) вероятности состояний.

Применительно к рассматриваемой задаче моделирования интерес представляет состояние – в системе выявлены обе уязвимости, характеризуемое вероятностью – это состояние, в котором создаются условия для осуществления атаки – выявлены и не устранены все уязвимости, необходимые для осуществления атаки.

Таким образом эту характеристику можем далее рассматривать в качестве вероятности возникновения угрозы атаки ( = ).

Заметим, что значение вероятности 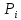(как предельной вероятности)показывает среднее относительное время пребывания системы в i–м состоянии. Используем это для моделирования остальных важнейших характеристик угрозы атаки.

Естественно, что имея значения параметров уязвимостей, создающих угрозу атаки, - интенсивности возникновения уязвимости 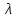, и устранения уязвимостиµ, в первую очередь, требуется определить соответствующие параметры (интенсивности возникновения и устранения) угрозы атаки в целом.

Вновь обратимся к графу, представленному на рис.2, для которого приняли = Как видим, угроза атаки создается в двух случаях - при переходе из состояния , в котором система находится с вероятностью , в состояние (это состояние угрозы атаки ), переходы осуществляются с интенсивностью ипри переходе из состояния , в котором система находится с вероятностью , в состояние , переходы осуществляются с интенсивностью . Оценим, каковы доли подобных переходов. За некоторый интервал времениT в состоянии в среднем система будет находиться в течение времени При интенсивности переходов в состояние из состояния , определяемой (на рассматриваемом интервале времениT ), в среднем будет осуществлено подобных переходов, соответственно из состояния в состояние будет осуществлено переходов. Долю переходов обозначим черезk:

Замечание. Рассматриваем отношение, при котором выполняется условие:k≤1.

Естественно, что соответствующим образом, см. рис.2, будут распределены и доли переходов (выходов) из состояния в состояния и с соответствующими интенсивностями и С учетом сказанного можем определить интенсивность устранения угрозы атаки :

Определив параметр угрозы атаки , и представив граф системы состояний случайного процесса с двумя состояниями (угроза атаки отсутствует) с вероятностью 1 - и (в системе создается угроза атаки) с вероятностью , переходы между состояниями определяются интенсивностями возникновения и устранения угрозы атаки, получим расчетную формулу для вычисления параметра интенсивности возникновения угрозы атаки :

Замечание. Для упрощения записей, в работе рассматривается пример графа, включающего всего четыре состояния, см. рис.2, т.е. угроза атаки, создаваемая двумя уязвимостями (группами уязвимостей).В общем случае для определения параметров и требуется анализировать фрагмент графа, включающий в себя вершины, из которых осуществляется непосредственный переход в вершину . Например, если угрозу атаки создают три уязвимости (группы уязвимостей) в анализируемый фрагмент графа включаются три вершины (и соответственно вершина ), описывающие состояния присутствия (выявления) в системе одновременно двух уязвимостей.

Средняя наработка на отказ. В теории надежности этот показатель относится к восстанавливаемым объектам, при эксплуатации которых допускаются многократно повторяющиеся отказы. Эксплуатация таких объектов может быть описана следующим образом: в начальный момент времени объект начинает работу и продолжает работу до первого отказа; после отказа происходит восстановление работоспособности, и объект вновь работает до отказа и т.д.

Если характеристику интерпретировать, как коэффициент готовностиинформационной системы к безопасной эксплуатации в отношении угрозы атаки, то средняя наработка на отказ – средняя продолжительность работы информационной между моментами появления в ней реальной угрозы соответствующей атаки :

В процессе эксплуатации информационной системы реальная угроза атаки продолжительностью 1/ в случае, если она не будет реализовываться нарушителем, в среднем через интервал времени будет многократно возникать, что можно отобразить в виде, представленном на рис.3.

Рис.3. Иллюстрация появления угрозы атаки в процессе эксплуатации

Информационной системы

2.3. Модель реализации нарушителем реальной угрозы атаки.

Введем следующую характеристику угрозы атаки - коэффициент готовности нарушителя осуществить конкретную атаку (атаку определенной сложности) на конкретную информационную систему где 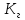≤ 1. Данная характеристика имеет физический смысл вероятности того, что при возникновении условий осуществления атаки, определяемых следующим образом: , нарушителем будет реализована эта атака. По сути, это уже характеристика нарушителя. Отметим, что построенная выше марковская модель соответствует условию: 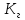= 0.

Замечание. В рамках интерпретации атаки соответствующим орграфом, см. рис.1, готовность нарушителя осуществить конкретную атаку можно рассматривать, как элемент уязвимости информационной системы, который может быть включен в орграф соответствующей вершиной, "взвешенной" значением и в качестве соответствующего дополнительного резервирующего элемента в схеме параллельного резерва, определяющим включение коэффициента 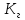в соответствующую расчетную формулу.

При проектировании систем защиты информационных систем (защищенных информационных систем) крайне важна оценка изменения вероятности возникновения угрозы атаки в процессе эксплуатации системы (естественно, что рассматриваем условие: 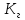<1). Например, реальные потери от внедрения и эксплуатации системы защиты в информационной системе растут с течением времени и через некоторый интервал времени ее эксплуатации могут превысить риск потерь от хищения обрабатываемой информации, что необходимо оценивать при проектировании системы защиты [///]. Подобное изменение обусловлено тем, что, как проиллюстрировано на рис.3, при условии 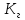<1 (где 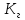интерпретируется, как вероятность того, что привозникновении условий осуществления атаки, определяемых следующим образом: , нарушителем будет реализована эта атака) в процессе эксплуатации системы нарушителю системой будет многократно предоставляться возможность осуществления атаки, посколькуугроза атаки средней продолжительностью 1/ в среднем через интервал времени .

Введем понятие периода эксплуатации информационной системы в отношении угрозы атаки В процессе эксплуатации нарушитель осуществит атаку в любом отдельно взятом периоде (по завершении периода, поскольку определяетсреднее время наработки информационной системы до появления в ней угрозы атаки) с вероятностью С учетом сказанного, интерес представляет оценка вероятности угрозы атаки и ее изменение за какое-либо время эксплуатации информационной системы, определяемое числом периодов эксплуатации (период эксплуатации определяется, каксреднее время наработки информационной системы до появления в ней угрозы атаки с использованием графа состояний, представленного на рис.1), обозначим По завершении первого периода эксплуатации - приi=1 - имеем по завершении второго , по завершении третьего и т.д.

Обозначим, через вероятность угрозы атаки возникающую за время эксплуатацииt информационной системы, включающем (по завершении) Iпериодов эксплуатации , i = 1,...,I, которая может быть рассчитана следующим образом:

Качественная зависимость изменения характеристики в процессе эксплуатации информационной системы, иллюстрирующая сказанное, представлена на рис.5.

Соответственно, рассчитать значение характеристики достигаемой при эксплуатации системы за некоторый произвольный интервалвремени (в момент времениt) при условии обозначим как следует из зависимости, представленной на рис.4, можно следующим образом:

где, как ⌉d⌈обозначено меньшее целое числа d.

Рис.4. Иллюстрация изменения характеристики в процессе эксплуатацииинформационной системы

На практике для расчета в любой момент времениt целесообразно использовать аппроксимирующую функцию. Основное правило аппроксимации при этом состоит в том, что значение аппроксимирующей функции для любогоt должно быть не меньше значения функции в соответствующий момент времениt – аппроксимирующая функция должна предоставлять возможность получения соответствующей граничной оценки, что требуется при проектировании системы защиты.

2.4. Модель угрозы атаки нарушителем на информационную систему при условии 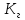= 1.

Построим модель системы, в которой нарушителем будет реализована реальная угроза атаки при первом же ее возникновении, что определяется, как Для рассмотренного ранее примера - угроза атаки создается двумя уязвимостями (группами уязвимостей), соответствующий граф системы состояний случайного процесса для анализируемого случая: 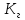= 1 (в отношении угрозы атаки система рассматривается, как система с отказами), представлен на рис.5.

Рис.5. Граф системы состояний случайного процесса для условия: 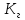= 1

В данном случае нас интересуют две характеристики - вероятность осуществления успешной атаки на информационную систему определяемая переходом в вершину исреднее время наработки информационной системы до осуществления на нее успешной атаки (средняя наработка до отказа – в отношении угрозы атаки система не восстанавливаемая). Как рассчитать характеристику было рассмотрено выше.Cистема дифференциальных уравнений Колмогорова для вероятностей состояний для данного графа будет иметь следующий вид:

Для определения же нужно уже рассчитать среднееабсолютное время пребывания системы в каждом i-м состояний , поскольку

Для вычисления среднего абсолютного времени пребывания системы в каждом i-м состояний , в системе уравнений Колмогорова нужно положить нулю все производные =0), кроме , если считать, что в начальный момент вероятность первого состояния =1. Тогда на основании теоремы о дифференцировании изображений в преобразовании Лапласа правая часть первого уравнения будет равна -1. В правых частях уравнений вместо 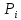, подставляются , и относительно них решается система алгебраических уравнений.

С учетом сказанного для рассматриваемого примера, применительно к графу, приведенному на рис.5, получаем следующую систему уравнений:

Решая данную систему уравнений, вычисляем искомые характеристики и соответственно среднее время наработки информационной системы до осуществления на нее успешной атаки .

Замечание. Для расчета требуемых значений достаточно использовать три первых уравнения.

2.5. Модель угрозы атаки нарушителем на информационную систему в общем случае - при условии 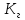≤ 1.

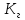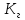Теперь рассмотрим общий случай, определяемый условием: ≤ 1. Данный случай характеризуется тем, что при возникновении условия реализации атаки - появления реальной угрозы атаки ( , атака будет реализована потенциальным нарушителем с вероятностью с вероятностью же 1 - атаки не произойдет, т.е. в системе будет переход к другому состоянию, в результат устранения соответствующей выявленной уязвимости. Учтем это условие включением вграф системы состояний случайного процесса, представленный на рис.1, вместо вершины двух вершин и , см. рис.6. Переход в вершину предполагает неготовность совершения атаки нарушителем при возникновении ее угрозы (поэтому для этой вершины присутствуют переходы в вершины и Переход в вершину характеризует реализацию атаки злоумышленником на информационную систему.

Рис.6. Граф системы состояний случайного процесса для условия: 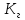<1

Замечание. При условии 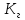= 1, граф, представленный на рис.6 сводится к графу, представленному на рис.5, при условии 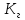=0 - к графу, представленному на рис.2.

Рассчитываются искомые характеристики (в данном случае нас интересуют вероятность осуществления успешной атаки на информационную систему определяемая переходом в вершину исреднее время наработки информационной системы до осуществления на нее успешной атаки (наработки до отказа информационной безопасности в отношении атаки) по аналогии с тем, как это было описано выше. Вероятность же, задаваемая переходом в вершину , определяет вероятность того, что в информационной системе возникнет реальная угроза атаки, которая не будет реализована нарушителем.

Замечание. Используя марковскую модель, проиллюстрированную рис.2, можно оценить среднее время наработки информационной системы между моментами появления в ней реальной угрозы атаки . Вычислив же среднее время наработки информационной системы до осуществления на нее успешной атаки , можно оценитьизменение характеристики в процессе эксплуатации информационной системы, см. рис.4.

Как было показано ранее, ключевым вопросом при моделировании угрозы атаки на информационную системы является определение коэффициента готовности нарушителя осуществить эту атаку на конкретную информационную систему 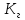, поскольку моделировать угрозу атаки в отношении некой абстрактной системы не имеет никакого смысла. По своей сути, при этом должна быть решена задача построения математической модели нарушителя[///].