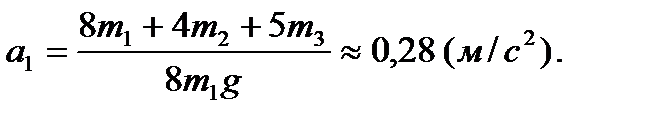Глава 4. дифференциальные урнения движения механической системы в обобщенных координатах

4.1. Общее уравнение динамики (принцип Даламбера-Лагранжа)

Принцип Даламбера-Лагранжа является комбинацией двух предыдущих принципов аналитической механики – принципа Даламбера и принципа возможных перемещений. Если ко всем точкам движущейся механической системы наряду с обычными силами приложить даламберовы силы инерции, то согласно принципу Даламбера получим уравновешенную систему сил. Для изучения такой системы сил можно применить принцип возможных перемещений. В результате получим принцип Даламбера-Лагранжа в следующей формулировке:

при движении механической системы сумма элементарных работ обычных сил и даламберовых сил инерции, приложенных к каждой точке системы, равна нулю на любом возможном перемещении системы из любого текущего положения.

Этот принцип можно выразить в виде уравнения:

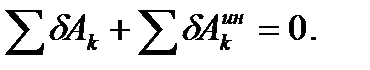(89)

Уравнение (89), выражающее принцип Даламбера-Лагранжа, называют общим уравнением динамики. Если механическая система имеет s степеней свободы, то аналогично принципу возможных перемещений из (89) можно получить s независимых уравнений движения механической системы в виде:

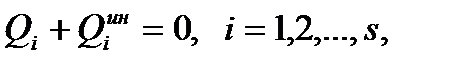(90)

где 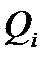- обобщенная сила для обычных сил, 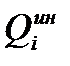- обобщенная сила для даламберовых сил инерции. Обе эти обобщенные силы соответствуют обобщенной координате .

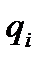Отметим, что каждое из уравнений (90) является дифференциальным уравнением второго порядка относительно обобщенных координат, так как 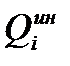вычисляются через ускорения точек системы, которые, в свою очередь, выражаются через вторые производные по времени от обобщенных координат.

Следует также иметь в виду, что при вычислении обобщенных сил 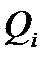нужно учитывать элементарную работу как внешних, так и внутренних сил механической системы. Работа внутренних сил будет равна нулю, если материальные тела, входящие в состав механической системы, абсолютно твердые и внутренние связи идеальные.

Пример 16

Груз 1 массой 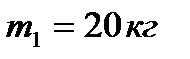опускается вниз, приводя в движение с помощью гибкой нерастяжимой нити однородный диск 3 радиусом R и массой 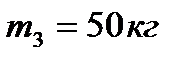(см. рис. 58). Нить намотана на диск 3 и переброшена

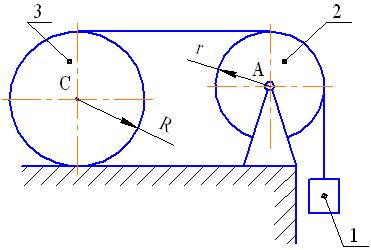
Рис. 58

через блок 2 массой 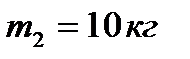. Диск 3 катится по опорной поверхности без проскальзывания. Блок 2 считать однородным диском радиуса r. Трением в оси блока пренебречь.

Определить ускорение груза 1.

Решение

Применим для решения задачи принцип Даламбера-Лагранжа. Тела, входящие в состав механической системы, абсолютно твердые и внутренние связи (гибкая нерастяжимая нить) идеальны. Поэтому общее уравнение динамики примет вид

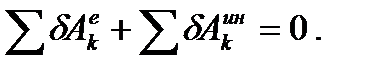
Обозначим на рис. 59 внешние активные силы 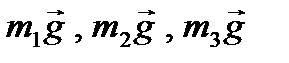и

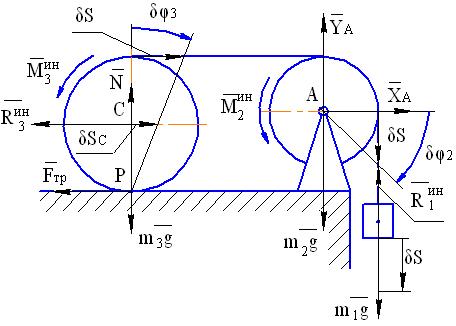
Рис. 59

реакции внешних связей 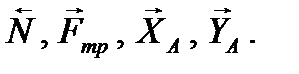Добавим к этим внешним силам даламберовы силы инерции. Для тела 1, движущегося поступательно, силы инерции точек тела заменим главным вектором 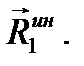Для тела 2, совершающего вращательное движение, главный вектор сил инерции 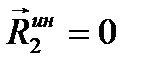(ускорение центра масс этого тела 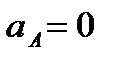), поэтому силы инерции точек тела 2 заменим парой сил с моментом 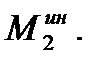Для тела 3, совершающего плоское движение, силы инерции его точек заменим главным вектором 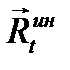и парой сил с моментом .

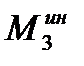Рассматриваемая механическая система имеет одну степень свободы. Поэтому, исходя из общего уравнения динамики, можно составить одно уравнение движения. Придадим системе возможное перемещение, мысленно сместив груз 1 вниз на расстояние 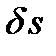. При этом блок 2 повернется на угол 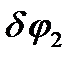вокруг оси вращения, диск 3 повернется на бесконечно малый угол 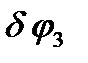вокруг мгновенного центра скоростей Р. Схема возможного перемещения показана на рис. 59.

Запишем теперь общее уравнение динамики:

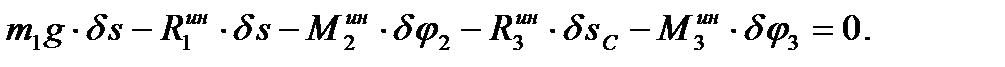(91)

Выразим все входящие в (91) перемещения через :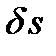

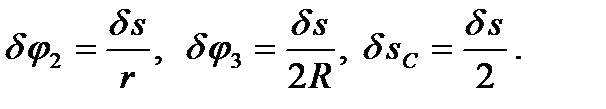(92)

Запишем выражения для главных векторов и главных моментов сил инерции: 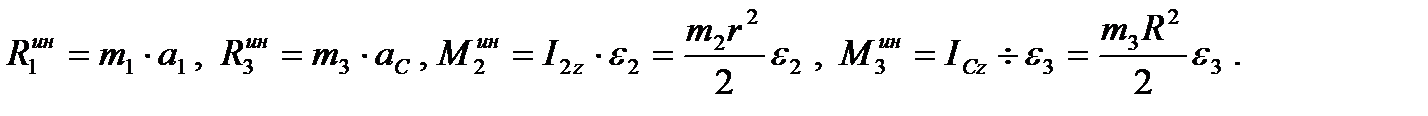(93)

Используя соотношения (92) между возможными перемещениями, выразим 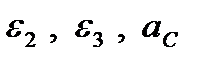через ускорение :

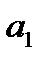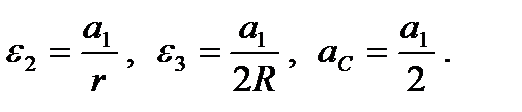
Подставим эти выражения в (93) и с учетом записанных формул перепишем общее уравнение динамики (91) в виде

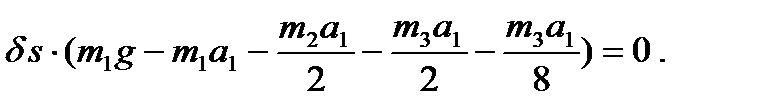
Так как 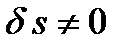, то должно быть равно нулю выражение в скобках:

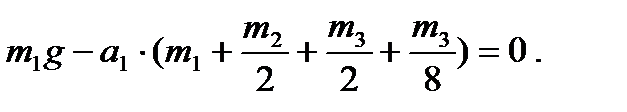
Отсюда найдем искомое ускорение груза 1: