Глава 2. принцип возможных перемещений

Общая формулировка принципа возможных перемещений

Принцип возможных перемещений (ПВП) выражает условие равновесия механической системы произвольного вида, находящейся под действием заданной системы активных сил и при заданных связях. Этот принцип впервые был сформулирован и доказан Лагранжем. Его также называют принципом Лагранжа или методом аналитической статики.

Для равновесия механической системы, подчиненной голономным, удерживающим, стационарным связям, необходимо и достаточно, чтобы на любом возможном перемещении системы из положения равновесия сумма элементарных работ всех сил, действующих на точки системы, равнялась нулю:

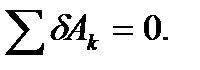(78)

Если связи, наложенные на механическую систему, являются идеальными, то работа их реакций на любом возможном перемещении системы равна нулю и при составлении уравнения (78) следует вычислять только работу активных сил, действующих на точки системы.

Пусть в равновесии находится механическая система, обладающая s степенями свободы. Тогда ее положение однозначно определяется обобщенными координатами 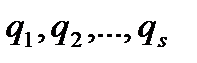, число которых равно s. Такой механической системе из положения равновесия можно придать s независимых возможных перемещений, при каждом из которых только одна обобщенная координата получает бесконечно малое приращение 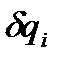, а остальные обобщенные координаты остаются неизменными::

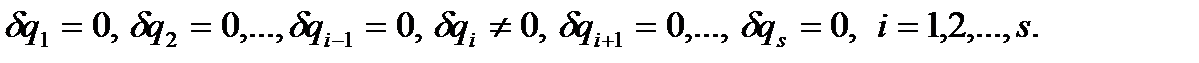
Записав уравнение (78) для каждого из таких перемещений, получим s независимых уравнений равновесия, выраженных через обобщенные силы, в виде:

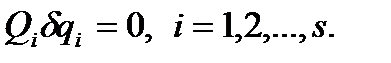
Так как 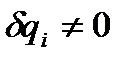, то уравнения равновесия системы в обобщенных силах примут вид

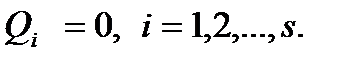(79)

Таким образом, в положении равновесия механической системы все ее обобщенные силы равны нулю.

Пример 11

На рис. 42 изображен находящийся в равновесии механизм, расположенный в горизонтальной плоскости. Трение в направляющих поршня С и шарнирах отсутствует. Заданы величина силы Q=200 Н,

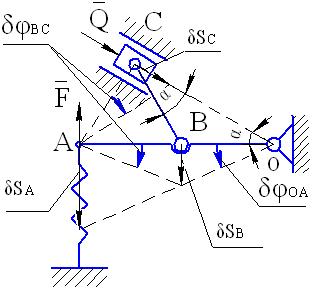
Рис. 42

коэффициент жесткости пружины с=5000 Н/м, 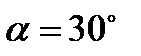, ОВ=АВ=l.

Требуется определить деформацию пружины h.

Решение

Механизм имеет одну степень свободы. Он находится в равновесии под действием заданной силы Q , приложенной к поршню С и силы упругости пружины, пропорциональной ее деформации F=ch. Выберем в качестве обобщенной координаты угол поворота стержня ОА вокруг оси вращения 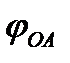, считая положительным направлением его отсчета поворот против часовой стрелки.

Решим задачу с помощью принципа возможных перемещений. Придадим механизму возможное перемещение, повернув стержень ОА вокруг оси вращения на угол 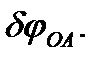Изобразим на рис. 42 схему возможного перемещения механизма, учитывая, что стержень ВС, совершающий плоское движение, повернется при этом перемещении на бесконечно малый угол 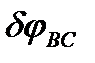вокруг мгновенного центра скоростей, расположенного в точке А.

Уравнение, выражающее принцип возможных перемещений, примет вид:

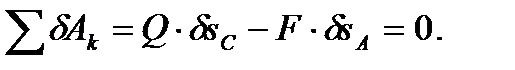(80)

Выразим входящие в это уравнение перемещения 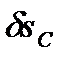и 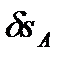через приращение обобщенной координаты 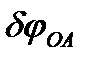. Перемещение точки А

.

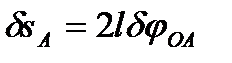Учитывая, что треугольник АВС равносторонний, для перемещения точки С получим

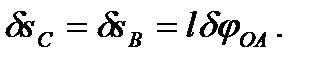
Подставляя эти значения перемещений и выражение для силы упругости в (80) и вынося 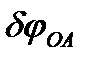за скобки, получим

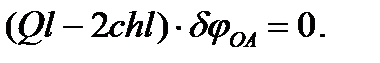
Здесь выражение в скобках является обобщенной силой, соответствующей обобщенной координате 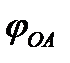. Отсюда получим ответ задачи

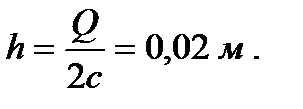
2.2. Применение принципа возможных перемещений для определения опорных реакций в статически определимых конструкциях

Выше рассмотрен случай использования принципа возможных перемещений для изучения равновесия механизма, который допускает возможные перемещения. Однако ПВП удобно использовать и для нахождения реакций в статически определимых конструкциях, которые нельзя мысленно перемещать, не нарушая наложенных связей.

В этом случае ПВП используется в сочетании с аксиомой связей. При этом реальная конструкция заменяется конструкцией, в которой одна из связей отброшена и ее действие заменено соответствующими реакциями. Такая конструкция с отброшенной связью уже допускает возможные перемещения и имеет число степеней свободы, соответствующее количеству компонент отброшенной связи. Используя ПВП, для такой измененной конструкции можно составить независимые уравнения равновесия, позволяющие найти все реакции отброшенной связи. Как правило, такие уравнения равновесия получаются более простыми по сравнению с уравнениями равновесия классической статики.

Для нахождения реакций другой связи нужно аналогичным образом рассмотреть еще одну воображаемую конструкцию с другой отброшенной связью.

Отметим, что принцип возможных перемещений удобно использовать при нахождении реакций опор для плоских конструкций. В пространственных задачах статики возникают сложности, когда требуется наглядно изобразить возможные перемещения.

Поясним изложенное на конкретном примере.

Пример 12

Требуется найти реакции опор и давление в промежуточном шарнире составной конструкции, изображенной на рис. 43. Заданы 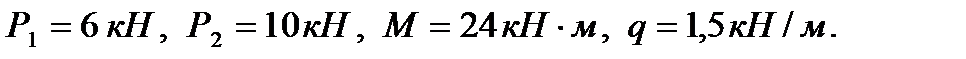Размеры указаны на чертеже в метрах.

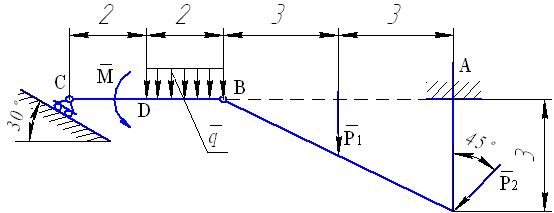
Рис. 43

Решение

Непрерывно распределенную на участке ВС нагрузку заменим равнодействующей силой Q=q·2=3 кН, приложенной в середине участка BD. Далее, поочередно отбрасывая связи, будем составлять уравнения равновесия с помощью ПВП.

1. Отбросим вначале подвижную шарнирную опору в точке С, заменив ее действие реакцией 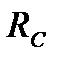(см. рис. 44). Конструкция получает

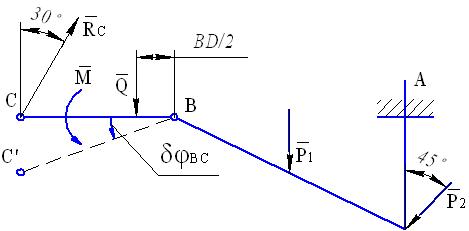
Рис. 44

при этом одну степень свободы. В качестве обобщенной координаты выберем угол поворота балки ВС 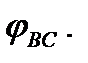Такой конструкции можно придать одно независимое возможное перемещение, повернув балку ВС на угол 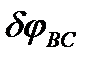вокруг точки В. Вычислим теперь сумму работ всех действующих на конструкцию сил на указанном возможном перемещении и приравняем ее нулю:

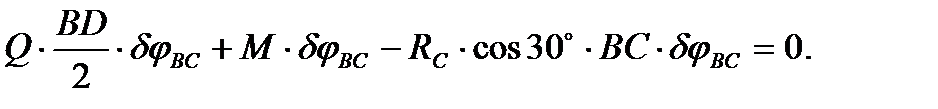
Отсюда

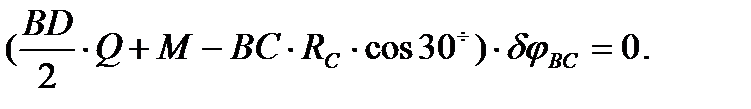
Так как то, приравняв нулю выражение в скобках, найдем

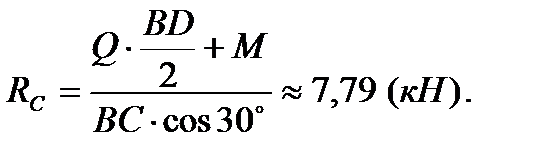
2. Для нахождения реакций в промежуточном шарнире В расчленим конструкцию, мысленно отбросив этот шарнир и сохранив опоры в токах А и С. После этого правая часть конструкции останется жестко закрепленной с помощью заделки в точке А и не допускающей возможных перемещений. Левая часть конструкции, балка ВС, получит при этом две степени свободы. Изобразим эту балку вместе с действующими на нее силами на рис. 45. Действие шарнира В, эквивалентного неподвижной шарнирной опоре, заменим реакцией, разложенной на две составляющих 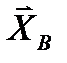и .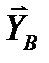

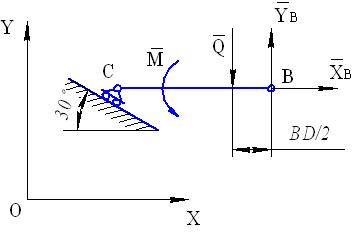
Рис. 45

В качестве обобщенных координат выберем декартовы координаты точки В 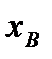и 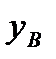. Не нарушая связи в точке С, придадим балке ВС два независимых возможных перемещения.

Первое из них получим, придав бесконечно малое приращение 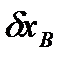обобщенной координате 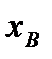и оставляя фиксированным значение обобщенной координаты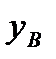 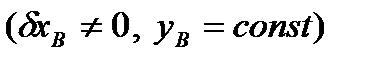. Плоское перемещение балки ВС при этом удобно представить как поворот на угол 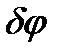вокруг мгновенного центра скоростей Р, лежащего на пересечении перпендикуляров к направлениям возможных перемещений точек С и В (см. рис. 46).

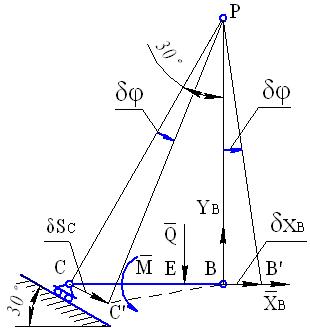
Рис. 46

Составим уравнение принципа возможных перемещений:

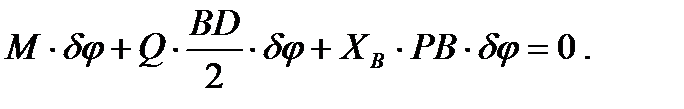
Вынося за скобки 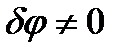, приравнивая нулю выражение в скобках и учитывая, что 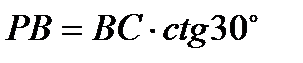, получим выражение

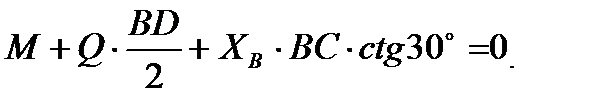
Отсюда

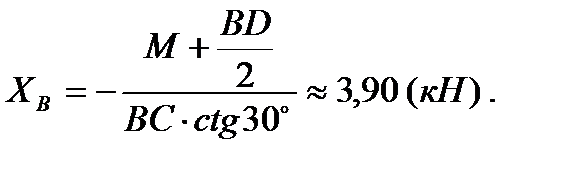
Второе независимое возможное перемещение (см. рис. 47) получим, зафиксировав обобщенную координату 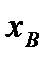и придав бесконечно малое приращение 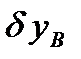обобщенной координате 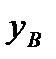( 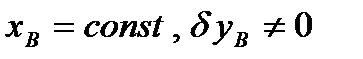). В этом

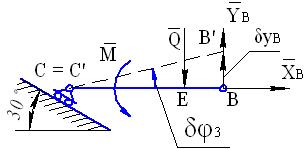
Рис. 47

случае мгновенный центр скоростей балки ВС совпадает с точкой С и уравнение принципа возможных перемещений запишется в виде:

Вынося за скобки 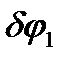и приравнивая нулю выражение в скобках, найдем

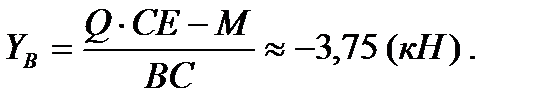
3. Для определения реакций заделки в точке А мысленно отбросим ее, заменив соответствующими реакциям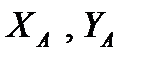и и 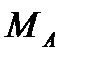( см. рис. 48 ). В

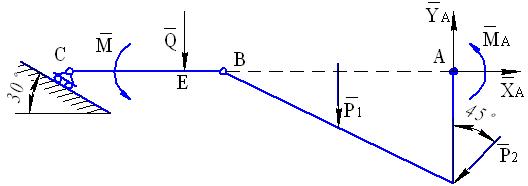
Рис. 48

этом случае конструкция имеет три степени свободы. В качестве обобщенных координат выберем декартовы координаты точки А - 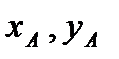и угол поворота уголка АВ - 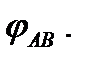Далее последовательно придадим этой конструкции три независимых возможных перемещения.

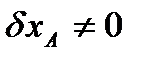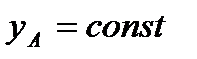Первое из них, характеризуемое приращением обобщенной координаты при и 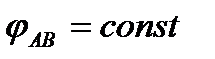схематически показано на рис. 49. Здесь уголок АВ перемещается поступательно в направлении оси x ( так как 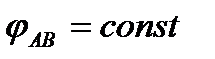), поэтому 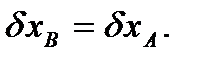Точка Р

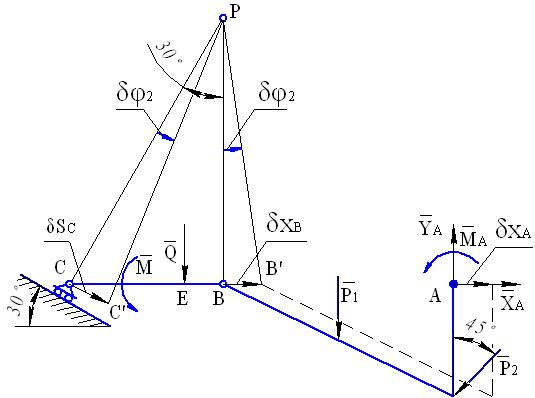
Рис. 49

является мгновенным центром скоростей звена ВС. Запишем для изображенного на рис. 49 возможного перемещения уравнение принципа Лагранжа:

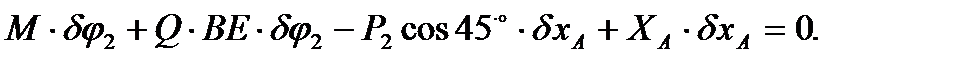
Выразим 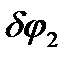через приращение обобщенной координаты :

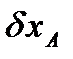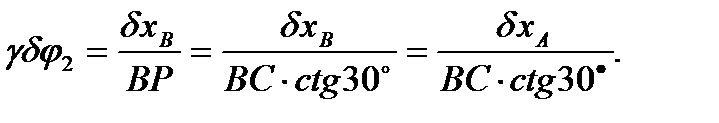
(Строго говоря, 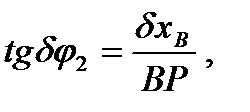но для бесконечно малого угла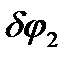 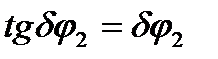). Подставив это значение 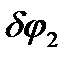в уравнение принципа Лагранжа, получим

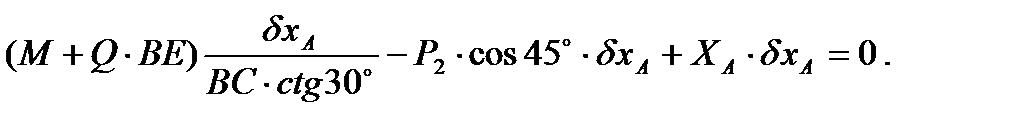
Вынося далее 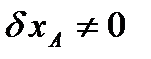за скобки и приравнивая выражение в скобках нулю, найдем

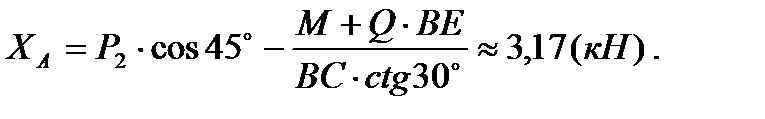
Второе независимое возможное перемещение рассматриваемой конструкции схематически показано на рис. 50. При этом перемещении

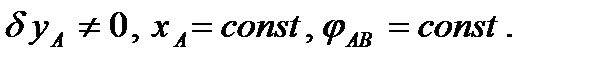Уголок АВ здесь перемещается

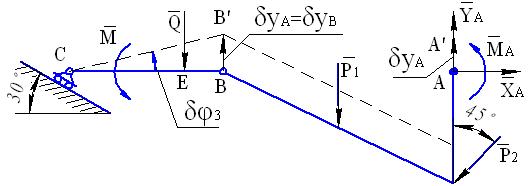
Рис. 50

поступательно ( так как 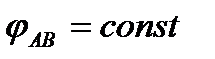) вдоль оси y, а мгновенный центр скоростей балки ВС совпадает с точкой С. Приравнивая нулю сумму работ всех сил на этом перемещении, получим:

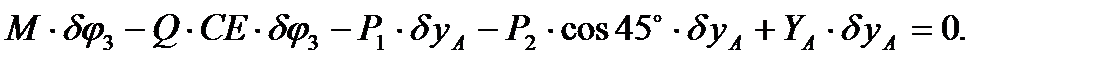
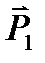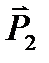Здесь учтено, что перемещения точек приложения сил и равны 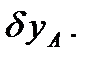Учитывая, что

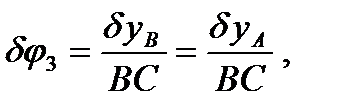
вынося 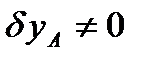за скобку и приравнивая нулю выражение в скобках, получим:

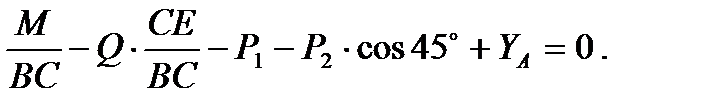
Отсюда найдем

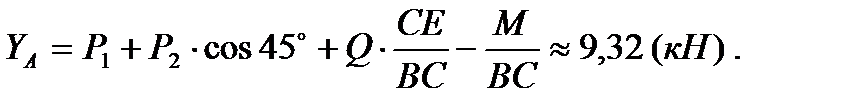
Последнее независимое возможное перемещение рассматриваемой конструкции схематически показано на рис. 51. При этом перемещении

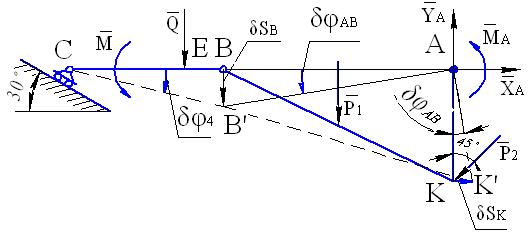
Рис. 51

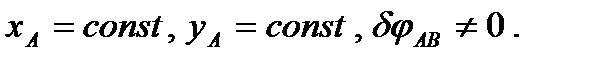Здесь уголок АВ поворачивается на бесконечно малый угол 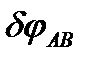вокруг точки А, а балка ВС поворачивается на угол 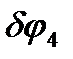вокруг мгновенного центра скоростей, совпадающего с точкой С. Запишем теперь уравнение принципа Лагранжа для изображенного возможного перемещения:

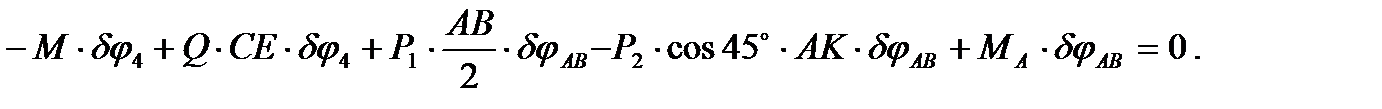
Связь между 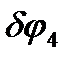и 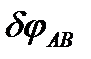найдем из условия

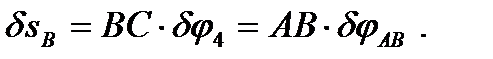
Отсюда

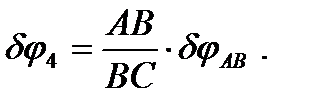
Подставляя это выражение для в записанное уравнение, вынося за скобки и приравнивая нулю выражение в скобках, получим

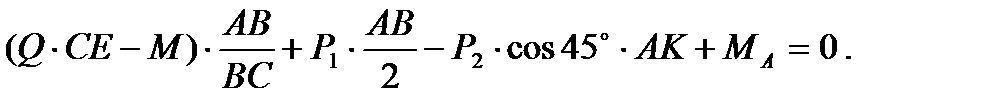
Отсюда найдем момент заделки

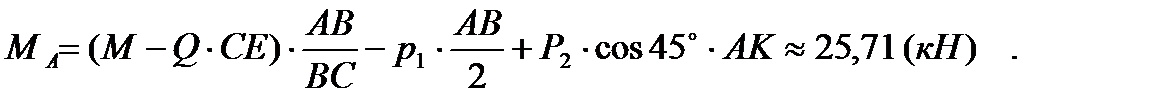
Одно из существенных преимуществ расчета статически определимых конструкций с помощью принципа возможных перемещений по сравнению с методами классической статики состоит в том, что каждое из получающихся уравнений содержит только одну неизвестную реакцию. Это значительно упрощает решение системы уравнений и, кроме того, позволяет, когда это необходимо, любую из искомых реакций независимо от остальных.

Глава 3. ПРИНЦИП ДАЛАМБЕРА

По своему содержанию этот принцип аналитической механики ничем не отличается от уравнений движения. Однако с его помощью уравнениям движения можно придать вид уравнений классической статики. В результате движение и равновесие материальных объектов можно изучать с помощью уравнений одинаковой структуры. На практике с помощью уравнений равновесия обычно находят реакции опор. Поэтому принцип Даламбера удобно использовать для нахождения опорных реакций в динамических условиях.