Деревья для симметричных матриц
Вес минимального остовного дерева, как мы уже знаем, дает оценку снизу, но ее можно улучшить. Остовное дерево состоит из 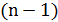 ребра, а гамильтонов цикл содержит
ребра, а гамильтонов цикл содержит 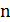 ребер. Добавление одного ребра к остовному дереву порождает так называемые
ребер. Добавление одного ребра к остовному дереву порождает так называемые
1-деревья. Они тоже дают нижние оценки. Итак, мы хотим найти гамильтонов цикл минимального веса, т. е. ровно 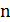 ребер, которые:
ребер, которые:
- покрывают все вершины и образуют связный граф,
- имеют минимальный суммарный вес,
- каждая вершина инцидентна ровно двум ребрам.
Ослабим последнее условие, заменив его следующим:
- одна заданная вершина инцидентна ровно двум ребрам.
Так как мы ослабили одно из условий, то получим нижнюю оценку. Алгоритм построения минимального по весу 1-дерева для выделенной вершины состоит в следующем. Удаляем эту вершину и смежные с ней ребра. На получившемся графе строим остовное дерево минимального веса. Получаем 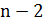 ребер. Добавляем два ребра, инцидентных выделенной вершине, имеющих минимальный суммарный вес. Полученное 1-дерево дает нижнюю оценку. Она зависит от выбора вершины. Построив 1-деревья для всех вершин и выбрав из нижних оценок наибольшую, получим требуемое.
ребер. Добавляем два ребра, инцидентных выделенной вершине, имеющих минимальный суммарный вес. Полученное 1-дерево дает нижнюю оценку. Она зависит от выбора вершины. Построив 1-деревья для всех вершин и выбрав из нижних оценок наибольшую, получим требуемое.
Задача о назначениях
Рассмотрим следующую задачу о назначении рабочих на станки [16, 21]. Дано: 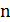 рабочих,
рабочих, 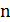 станков и матрица
станков и матрица 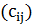 , задающая время выполнения работы на
, задающая время выполнения работы на 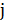 -м станке
-м станке 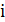 -м рабочим. Требуется найти расстановку рабочих по станкам, которая дает наименьшее суммарное рабочее время. Введем переменные задачи
-м рабочим. Требуется найти расстановку рабочих по станкам, которая дает наименьшее суммарное рабочее время. Введем переменные задачи 
Задача о назначениях может быть записана в следующем виде: 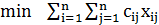 , при ограничениях
, при ограничениях 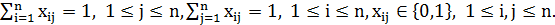
Сравнивая эту запись с аналогичной записью для задачи коммивояжера, легко заметить, что они отличаются только одной группой ограничений для исключения подциклов. Следовательно, оптимальное решение задачи о назначениях дает нижнюю оценку для задачи коммивояжера.
Приведем точный полиномиальный алгоритм решения задачи о назначениях. Пусть 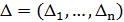 – некоторый вектор. Элемент
– некоторый вектор. Элемент  называется
называется  -минимальным для строки
-минимальным для строки 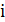 , если
, если 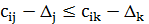 для всех
для всех 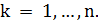
Теорема 5.8. Пусть для некоторого вектора  существует набор
существует набор  -минимальных элементов
-минимальных элементов  по одному в каждой строке и каждом столбце. Тогда этот набор является оптимальным решением задачи о назначениях.
по одному в каждой строке и каждом столбце. Тогда этот набор является оптимальным решением задачи о назначениях.
Доказательство. Решение  является допустимым, и
является допустимым, и 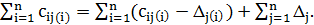
В правой части равенства первая сумма является минимальной среди всех допустимых назначений. Вторая сумма является константой. Значит, полученное решение является оптимальным. ∎
Определение 5.1. Для вектора  выделим в каждой строке по одному
выделим в каждой строке по одному  -минимальному элементу и назовем его
-минимальному элементу и назовем его  -основой. Другие
-основой. Другие  -минимальные элементы будем называть альтернативными
-минимальные элементы будем называть альтернативными
 -основами. Число столбцов матрицы
-основами. Число столбцов матрицы 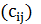 без
без  -основ назовем дефектом.
-основ назовем дефектом.
Идея алгоритма состоит в следующем. Начинаем с нулевого вектора  и считаем дефект. На каждом этапе алгоритма дефект уменьшается на 1, то есть не более чем за
и считаем дефект. На каждом этапе алгоритма дефект уменьшается на 1, то есть не более чем за 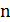 этапов получим оптимальное решение.
этапов получим оптимальное решение.
Описание одного этапа
1. Выберем столбец без  -основы и обозначим его
-основы и обозначим его 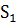 .
.
2. Увеличим 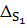 на максимальное
на максимальное 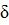 так, чтобы все
так, чтобы все
 -минимальные элементы остались
-минимальные элементы остались  -минимальными (возможно
-минимальными (возможно 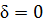 ). Получим для некоторой строки
). Получим для некоторой строки  новый
новый  -минимальный элемент
-минимальный элемент 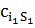 , назовем его альтернативной основой для строки
, назовем его альтернативной основой для строки  (рис. 5.13).
(рис. 5.13).
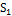 |
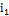 |
Рисунок-5.13. Появление альтернативной основы
3. Для строки  столбец
столбец 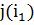 с
с  -основой пометим меткой
-основой пометим меткой 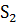 . (рис. 5.14).
. (рис. 5.14).
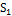 |
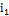 |
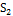 |
Рисунок-5.14. Выбор второго столбца
4.
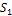 |
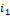 |
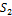 |
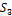 |
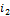 |
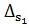 и
и 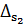 на максимальное
на максимальное 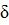 так, чтобы все
так, чтобы все  -основы остались
-основы остались  -минимальными элементами. Найдем новую альтернативную основу в одном из столбцов
-минимальными элементами. Найдем новую альтернативную основу в одном из столбцов 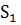 или
или 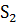 . Пусть она оказалась в строке
. Пусть она оказалась в строке 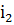 . Пометим столбец
. Пометим столбец 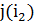 меткой
меткой 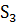 (рис. 5.15) и будем продолжать этот процесс до тех пор, пока не встретим столбец с двумя или более основами.
(рис. 5.15) и будем продолжать этот процесс до тех пор, пока не встретим столбец с двумя или более основами. Рисунок-5.15. Получение новой основы
5. Строим новый набор  -основ. Заменой основы в строке назовем следующую операцию: альтернативная основа становится основой, а старая перестает быть основой. Произведем замену основ в строке, где лежит последняя альтернативная основа (строка
-основ. Заменой основы в строке назовем следующую операцию: альтернативная основа становится основой, а старая перестает быть основой. Произведем замену основ в строке, где лежит последняя альтернативная основа (строка 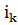 ). Тогда в столбце
). Тогда в столбце 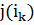 число основ уменьшится на 1, но останется положительным (рис. 5.16).
число основ уменьшится на 1, но останется положительным (рис. 5.16).
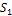 |
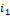 |
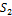 |
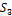 |
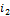 |
Рисунок-5.16. Замена основы
В столбце, где появилась новая основа, возьмем старую основу и в этой строке тоже проведем замену основ и так будем переходить от одного столбца к другому, пока не доберемся до столбца 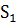 . В итоге, столбец
. В итоге, столбец 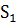 получит основу, а число основ в столбце
получит основу, а число основ в столбце 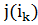 уменьшится на 1 (рис. 5.17).
уменьшится на 1 (рис. 5.17).
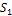 |
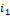 |
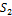 |
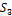 |
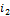 |
Рисунок-5.17. Новое распределение основ
Посчитаем трудоемкость одного этапа. Мы последовательно рассматриваем сначала один столбец 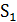 , затем два столбца
, затем два столбца 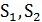 и т. д. Всего шагов может быть не больше n. На каждом шаге надо выбрать
и т. д. Всего шагов может быть не больше n. На каждом шаге надо выбрать 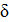 , что требует
, что требует 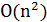 операций. Значит, всего требуется
операций. Значит, всего требуется 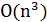 операций для одного этапа и
операций для одного этапа и 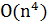 операций для всего алгоритма.
операций для всего алгоритма.
Локальный поиск
Идеи локального поиска при решении задач дискретной оптимизации являются, по-видимому, наиболее естественными и наглядными. Первые шаги их реализации относятся к началу 50-х, началу 60-х годов XX столетия. Они связаны, в основном, с задачей коммивояжера. Позднее эти идеи использовались для задач размещения, построения сетей, расписаний и др. Однако, довольно быстро выяснилось, что методы локального улучшения не гарантируют нахождения глобального оптимума, и отсутствие концептуального прогресса ослабило интерес к данному направлению. В последние 20 лет наблюдается возрождение этого подхода. Оно связано как с новыми алгоритмическими схемами, построенными на аналогиях с живой и неживой природой, так и с новыми теоретическими результатами в области локального поиска. Изменился общий взгляд на построение локальных алгоритмов. Требование монотонного улучшения по целевой функции больше не является доминирующим. Наиболее мощные алгоритмы допускают произвольное ухудшение, и многие из них могут рассматриваться как способ порождения конечных неразложимых цепей Маркова на подходящем множестве состояний. В данном разделе приводится краткое введение в эту бурно развивающуюся область дискретной оптимизации.
5.4.1. Основные определения
Пусть тройка 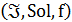 задает задачу дискретной оптимизации с множеством входов
задает задачу дискретной оптимизации с множеством входов 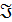 (исходных данных), конечным множеством допустимых решений
(исходных данных), конечным множеством допустимых решений 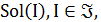 и целевой функцией
и целевой функцией 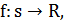
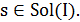 Для определенности будем считать, что требуется найти минимум функции f на множестве
Для определенности будем считать, что требуется найти минимум функции f на множестве 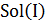 и само решение
и само решение 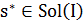 , на котором этот минимум достигается. Решение
, на котором этот минимум достигается. Решение 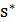 будем называть глобальным минимумом и множество глобальных минимумов будем обозначать через
будем называть глобальным минимумом и множество глобальных минимумов будем обозначать через 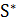 . Для каждого
. Для каждого 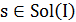 определим функцию окрестности
определим функцию окрестности 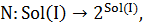 которая для каждого допустимого решения задает множество соседних решений, в некотором смысле близких к данному. Множество
которая для каждого допустимого решения задает множество соседних решений, в некотором смысле близких к данному. Множество 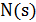 будем называть окрестностью решения
будем называть окрестностью решения 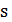 в множестве
в множестве 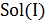 . Функция окрестности может быть достаточно сложной, и отношение соседства не всегда симметрично.
. Функция окрестности может быть достаточно сложной, и отношение соседства не всегда симметрично.
Определение 5.2.Решение 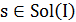 называется локальным минимумом по отношению к функции
называется локальным минимумом по отношению к функции  , если
, если 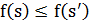 для всех
для всех 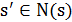 .
.
Множество локальных минимумов обозначим через 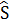 . Это множество, очевидно, зависит от выбора функции
. Это множество, очевидно, зависит от выбора функции 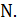
Определение 5.3.Функция окрестности  называется точной, если
называется точной, если 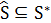 .
.
Стандартный алгоритм локального улучшения начинает работу с некоторого начального решения, выбранного случайным образом или с помощью какого-либо вспомогательного алгоритма. На каждом шаге локального улучшения происходит переход от текущего решения к соседнему решению с меньшим значением целевой функции до тех пор, пока не будет достигнут локальный минимум.
Алгоритмы локального улучшения широко применяются для решения NP-трудных задач. Многие полиномиально разрешимые задачи могут рассматриваться как задачи, легко решаемые таким способом. При подходящем выборе полиномиальной окрестности соответствующая теорема может быть сформулирована в следующем виде: допустимое решение не является глобальным оптимумом, если и только если оно может быть улучшено некоторым локальным образом. Ниже приводится несколько примеров таких задач. Они указывают на важность локального поиска при построении оптимизационных алгоритмов и достаточно общий характер этого подхода.
1. Линейное программирование. Геометрически алгоритм симплекс метода можно интерпретировать как движение по вершинам многогранника допустимой области. Вершина не является оптимальной, если и только если существует смежная с ней вершина с меньшим значением целевой функции. Алгебраически, предполагая невырожденность задачи, базисное допустимое решение не является оптимальным, если и только если оно может быть улучшено локальным изменением базиса, т. е. заменой одной базисной переменной на небазисную. Получающаяся таким образом окрестность является точной и имеет полиномиальную мощность.
2. Минимальное остовное дерево. Остовное дерево не является оптимальным, если и только если локальной перестройкой, добавляя одно ребро и удаляя из образовавшегося цикла другое ребро, можно получить новое остовное дерево с меньшим суммарным весом. Операция локальной перестройки задает отношение соседства на множестве остовных деревьев. Окрестность любого дерева имеет полиномиальную мощность, а функция окрестности является точной.
3. Максимальное паросочетание. Паросочетание не является максимальным, если и только если существует увеличивающий путь. Два паросочетания называют соседними, если их симметрическая разность образует путь. Определенная таким образом окрестность является точной и имеет полиномиальную мощность. Аналогичные утверждения справедливы для взвешенных паросочетаний, совершенных паросочетаний минимального веса, задач о максимальном потоке и потоке минимальной стоимости.
На каждом шаге локального улучшения функция окрестности задает множество возможных направлений движения. Часто это множество состоит из нескольких элементов и имеется определенная свобода в выборе следующего решения. Правило выбора может оказать существенное влияние на трудоемкость алгоритма и результат его работы. Например, в задаче о максимальном потоке алгоритм Форда – Фалкерсона (который тоже можно рассматривать как вариант локального улучшения) имеет полиномиальную временную сложность при выборе кратчайшего пути для увеличения потока и экспоненциальную временную сложность без гарантии получить глобальный оптимум при произвольном выборе пути. Таким образом, при разработке алгоритмов локального поиска важно не только правильно определить окрестность, но и верно задать правило выбора направления спуска.
Интуитивно кажется, что в окрестности надо брать элемент с наименьшим значением целевой функции. Однако, как мы увидим ниже, разумным оказывается не только такой выбор, но и движение в «абсурдном» направлении, когда несколько шагов с ухудшением могут привести (и часто приводят) к лучшему локальному минимуму. При выборе окрестности хочется иметь как можно меньше соседей, чтобы сократить трудоемкость одного шага. С другой стороны, более широкая окрестность, вообще говоря, приводит к лучшему локальному оптимуму. Поэтому при создании алгоритмов каждый раз приходится искать оптимальный баланс между этими противоречивыми факторами. Ясных принципов разрешения этих противоречий на сегодняшний день нет, и для каждой задачи этот вопрос решается индивидуально.
Определение 5.4.Графом соседства 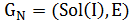 будем называть взвешенный ориентированный граф, вершинами которого являются допустимые решения задачи, а дугами – упорядоченные пары
будем называть взвешенный ориентированный граф, вершинами которого являются допустимые решения задачи, а дугами – упорядоченные пары 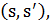 если
если 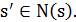 Веса в этом графе приписаны вершинам и равны соответствующим значениям целевой функции.
Веса в этом графе приписаны вершинам и равны соответствующим значениям целевой функции.
Граф соседства 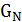 (neighborhood graph) иногда называют ландшафтом целевой функции или просто ландшафтом (landscape, fitness landscape). При определении функции окрестности важно следить за тем, чтобы получающийся граф был строго связен, то есть для каждой пары вершин
(neighborhood graph) иногда называют ландшафтом целевой функции или просто ландшафтом (landscape, fitness landscape). При определении функции окрестности важно следить за тем, чтобы получающийся граф был строго связен, то есть для каждой пары вершин 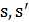 существовал путь из
существовал путь из 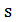 в
в 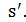 Это свойство является важным при анализе асимптотического поведения алгоритмов, например, вероятностных метаэвристик, о которых пойдет речь ниже. Если же это свойство не выполняется, то стараются получить хотя бы свойство вполне связности, когда из любой вершины существует путь в вершину
Это свойство является важным при анализе асимптотического поведения алгоритмов, например, вероятностных метаэвристик, о которых пойдет речь ниже. Если же это свойство не выполняется, то стараются получить хотя бы свойство вполне связности, когда из любой вершины существует путь в вершину 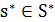 . Если же и этого свойства нет, то теряется уверенность в достижении глобального оптимума локальными методами. Приходится ограничиваться локальными оптимумами, либо переопределять функцию окрестности.
. Если же и этого свойства нет, то теряется уверенность в достижении глобального оптимума локальными методами. Приходится ограничиваться локальными оптимумами, либо переопределять функцию окрестности.
Анализ эффективности локального поиска условно можно разделить на два направления: эмпирические и теоретические исследования. Как это ни странно, но они дают разные оценки возможностям этого подхода [19, 20].
Эмпирические результаты. Для многих NP-трудных задач локальный поиск позволяет находить приближенные решения, близкие по целевой функции к глобальному оптимуму. Трудоемкость алгоритмов часто оказывается полиномиальной, причем степень полинома достаточно мала. Так, для задачи о разбиении множества вершин графа на две равные части разработаны алгоритмы локального поиска минимизации разреза со средней трудоемкостью 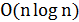 , которые дают всего несколько процентов погрешности.
, которые дают всего несколько процентов погрешности.
Для задачи коммивояжера алгоритмы локального поиска являются наилучшими с практической точки зрения. Один из таких алгоритмов с окрестностью Лина – Кернигана в среднем имеет погрешность около 2 %, и максимальная размерность решаемых задач достигает 1 000 000 городов. На случайно сгенерированных задачах такой колоссальной размерности итерационная процедура Джонсона позволяет находить решения с отклонением около 0,5 % за несколько минут на современных компьютерах.
Для задач теории расписаний, размещения, покрытия, раскраски графов и многих других NP-трудных задач алгоритмы локального поиска показывают превосходные результаты. Более того, их гибкость при изменении математической модели, простота реализации и наглядность превращают локальный поиск в мощное средство для решения практических задач.
Теоретические результаты. Исследование локального поиска с точки зрения гарантированных оценок качества показывают границы его возможностей. Построены трудные для локального поиска примеры, из которых следует, что:
1) минимальная точная окрестность может иметь экспоненциальную мощность;
2) число шагов для достижения локального оптимума может оказаться экспоненциальным;
3) значение локального оптимума может сколь угодно сильно отличаться от глобального оптимума.
Эти результаты подталкивают к более пристальному рассмотрению задачи нахождения локального оптимума, ее трудоемкости в среднем и худшем случаях. Абстрактная (массовая) задача локального поиска  задается множеством ее индивидуальных примеров, каждый из которых однозначно определяет целевую функцию, функцию окрестности и множество допустимых решений.
задается множеством ее индивидуальных примеров, каждый из которых однозначно определяет целевую функцию, функцию окрестности и множество допустимых решений.
Определение 5.5. Задача 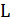 принадлежит классу PLS (polynomial time local search), если за полиномиальное время от длины записи исходных данных можно выполнить следующие три операции:
принадлежит классу PLS (polynomial time local search), если за полиномиальное время от длины записи исходных данных можно выполнить следующие три операции:
1) Для произвольного примера 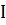 проверить его корректность и, если
проверить его корректность и, если 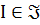 , найти некоторое допустимое решение.
, найти некоторое допустимое решение.
2) Для любого решения проверить, является ли оно допустимым и, если да, вычислить значение целевой функции для него.
3) Узнать, является ли данное решение локальным оптимумом и, если нет, найти в его окрестности решение с лучшим значением целевой функции.
Грубо говоря, в классе PLS содержатся все задачи локального поиска, для которых проверка локальной оптимальности может быть осуществлена за полиномиальное время. Этот класс не пуст, так как задача коммивояжера с окрестностью 2-замена содержится в нем. Следующая теорема говорит о том, что, скорее всего, в этом классе нет NP-трудных задач.
Теорема 5.9.Если задача  из класса PLS является NP-трудной, то NP = co-NP.
из класса PLS является NP-трудной, то NP = co-NP.
В классе PLS содержатся полиномиально разрешимые задачи, то есть задачи, для которых можно найти локальный оптимум за полиномиальное время. Многие NP-трудные задачи без весовых функций с любой полиномиально проверяемой окрестностью относятся к таковым: задачи о клике, о покрытии, о независимом множестве и др. Задача коммивояжера с матрицей 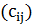 , состоящей из 1 и 2, будет таковой при любой полиномиально проверяемой окрестности. Однако, в общем случае вопрос о вычислительной сложности нахождения локального оптимума пока остается открытым. Так же, как и для задач распознавания, в классе PLS можно определить сведение одной задачи к другой и доказать теорему о существовании PLS-полных задач. Это наиболее трудные задачи в этом классе. Существование полиномиального алгоритма хотя бы для одной из них влечет полиномиальную разрешимость для всех задач из класса PLS. Задача коммивояжера с окрестностью k-замена является PLS-полной при
, состоящей из 1 и 2, будет таковой при любой полиномиально проверяемой окрестности. Однако, в общем случае вопрос о вычислительной сложности нахождения локального оптимума пока остается открытым. Так же, как и для задач распознавания, в классе PLS можно определить сведение одной задачи к другой и доказать теорему о существовании PLS-полных задач. Это наиболее трудные задачи в этом классе. Существование полиномиального алгоритма хотя бы для одной из них влечет полиномиальную разрешимость для всех задач из класса PLS. Задача коммивояжера с окрестностью k-замена является PLS-полной при 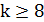 . Более того, удается показать, что стандартный алгоритм локального улучшения для этой задачи требует в худшем случае экспоненциального числа итераций независимо от того, какое правило замещения будет применяться. Более подробно с теорией PLS-полных задач можно познакомиться в [23, 25].
. Более того, удается показать, что стандартный алгоритм локального улучшения для этой задачи требует в худшем случае экспоненциального числа итераций независимо от того, какое правило замещения будет применяться. Более подробно с теорией PLS-полных задач можно познакомиться в [23, 25].
