Тема 4. Нелинейный регрессионный анализ

БЛОК 1

1. Известно, что с увеличением объема производства себестоимость единицы продукции уменьшается за счет того, что происходит перераспределение постоянных издержек. Пусть a – совокупная величина постоянных издержек, а b – величина переменных издержек в расчете на одно изделие. Тогда зависимость себестоимости единицы продукции от объема производства можно описать с помощью модели …

○ ,

○ ,

○ ,

○ .

2. Коэффициент детерминации для нелинейной модели определяется как …

○ отношение дисперсии расчетных значений зависимой переменной к дисперсии ее наблюдаемых значений,

○ отношение дисперсии логарифмов расчетных значений зависимой переменной к дисперсии логарифмов ее наблюдаемых значений,

○ отношение дисперсии отклонений к дисперсии наблюдаемых значений зависимой переменной,

○ отношение дисперсии преобразованных расчетных значений зависимой переменной к дисперсии наблюдаемых значений.

3. Модель Филипса служит для описания зависимости …

○ уровня безработицы от изменения заработной платы,

○ спроса на товары различных групп от дохода,

○ прибыли от расходов на рекламу,

○ объема выпуска от затрат капитала и труда.

4. Оценить статистическую значимость нелинейной связи между переменными можно с помощью …

○ средней ошибки аппроксимации,

○ индекса корреляции,

○ критерия Фишера,

○ индекса детерминации.

5. Экспоненциальным не является уравнение регрессии …

○ ,

○ ,

○ ,

○ .

6. При выборе спецификации нелинейная регрессия используется, если …

○ между экономическими показателями обнаруживается линейная зависимость,

○ между экономическими показателями не обнаруживается нелинейная зависимость,

○ нелинейная зависимость для исследуемых экономических показателей является несущественной,

○ между экономическими показателями обнаруживается нелинейная зависимость.

7. Обратной является эконометрическая модель вида …

○ ,

○ ,

○ ,

○ .

8. Нелинейная связь между рассматриваемыми признаками тем теснее, чем значение индекса корреляции ближе к …

○ 0,

○ -1,

○ ,

○ 1.

9. Использование полинома второго порядка в качестве регрессионной зависимости для однофакторной модели обусловлено …

○ отсутствием тенденции,

○ неоднородностью выборки,

○ изменением направления связи результирующего и факторного признаков,

○ наличием случайных колебаний.

10. Нелинейное уравнение регрессии означает нелинейную форму зависимости между …

○ фактором и случайной величиной,

○ результатом и параметрами,

○ фактором и результатами,

○ результатом и факторами.

11. Примером нелинейной зависимости экономических показателей является …

○ классическая гиперболическая зависимость спроса от цены

○ линейная зависимость выручки от величины оборотных средств

○ зависимость объема продаж от недели реализации, выраженная линейным трендом

○ линейная зависимость затрат на производство от объема выпуска продукции.

12. Линеаризация экспоненциальной зависимости (кривой Энгеля, отражающей зависимость спроса от уровня семейных доходов) основана на …

○ интегрировании функции по параметрам

○ разложении функции в ряд

○ дифференцировании функции по параметрам

○ логарифмировании и замене преобразованной переменной.

13. Примером нелинейной зависимости экономических показателей является …

○ классическая гиперболическая зависимость спроса от цены

○ линейная зависимость выручки от величины оборотных средств

○ зависимость объема продаж от недели реализации, выраженная линейным трендом

○ линейная зависимость затрат на производство от объема выпуска продукции.

14. Нелинейным является уравнение регрессии нелинейное относительно входящих в него …

○ случайных величин

○ параметров

○ факторов

○ результатов.

15. Кривая Энгеля, характеризующая отношение между доходами семьи (x) и долей доходов, расходуемых на продовольствие (y) является …

○ убывающей функцией с нижней горизонтальной асимптотой y=a,

○ убывающей функцией с верхней горизонтальной асимптотой y=a,

○ возрастающей функцией с нижней горизонтальной асимптотой y=a,

○ возрастающей функцией с верхней горизонтальной асимптотой y=a.

16. Нелинейным как по переменным, так и по параметрам не является уравнение вида…

○

○

○

○ .

17. Зависимость общих издержек от объема выпуска продукции в микроэкономике характеризуется степенной эконометрической моделью …

○

○

○

○

18. Экспоненциальной является эконометрическая модель вида …

○

○

○

○ .

19. Если между экономическими показателями существует нелинейная связь, то …

○ нецелесообразно использовать спецификацию нелинейного уравнения регрессии,

○ целесообразно использовать спецификацию нелинейного уравнения регрессии,

○ необходимо включить в модель другие факторы и использовать линейное уравнение множественной регрессии,

○ целесообразно использовать линейное уравнение парной регрессии.

20. В нелинейной модели парной регрессии функция f(x) является …

○ линейной,

○ равной нулю,

○ нелинейной,

○ несущественной.

21. Зависимость валового национального продукта (Y) от денежной массы (Х) характеризуется линейно-логарифмической эконометрической моделью, которая имеет вид …

○

○

○

○ .

22. Полиномиальной является эконометрическая модель вида …

○

○

○

○ .

БЛОК 2

1. В эконометрическую модель линейным образом включены …

□ параметр а,

□ переменная х,

□ переменная y,

□ параметр b.

2. Укажите верные утверждения по поводу модели :

□ относится к типу нелинейных моделей внутренне нелинейных (которые нельзя привести к линейному виду),

□ линеаризуется в линейную модель парной регрессии,

□ относится к типу нелинейных моделей внутренне линейных (которые можно привести к линейному виду),

□ линеаризуется в линейную модель множественной регрессии.

3. В эконометрическую модель вида Кобба-Дугласа линейным образом включены…

□ параметр а,

□ переменная ,

□ переменная ,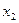

□ переменная y.

4. Укажите верные утверждения по поводу модели :

□ относится к типу нелинейных моделей внутренне нелинейных (которые нельзя привести к линейному виду),

□ оценки параметров регрессии нельзя определить с помощью МНК,

□ линеаризуется в линейную модель парной регрессии,

□ относится к типу нелинейных моделей линейных по параметрам.

5. Примерами нелинейных уравнений регрессии, которые могут быть приведены к линейному виду, являются:

□ ,

□ ,

□ ,

□ .

6. Примерами нелинейных уравнений регрессии, нелинейных по оцениваемым параметрам, являются:

□ ,

□ ,

□ ,

□ .

7. Укажите последовательность этапов оценки параметров нелинейной регрессии .

2 задается спецификация модели в виде , где

3 оцениваются параметры регрессии b₀, b₁, b₂

4 определяются исходные параметры из тождеств:

1 выполняется замена переменной X² на Z.

8. Примерами уравнений регрессии, нелинейных относительно объясняющих переменных, но линейных по оцениваемым параметрам являются:

□

□

□

□

9. Диаграмма рассеяния указывает на нелинейную зависимость. В этом случае следует осуществить …

□ подбор преобразования переменных, дающего наибольшее по абсолютной величине значение коэффициента парной корреляции

□ включение в модель дополнительных факторных признаков

□ визуальный подбор функциональной зависимости нелинейного характера, соответствующего структуре точечного графика

□ расчет линейного коэффициента корреляции и использование линейной модели.

10. Установите соответствие между названием модели и видом ее уравнения.

1. линейная
2. полиномиальная
3. показательная
4. степенная

3

1

4

2 .

11. Пусть зависимость выпуска ( ) от затрат капитала ( ) и труда ( ) описывается функцией Кобба-Дугласа . Тогда …

□ эластичность выпуска по затратам капитала равна

□ эластичность выпуска по затратам капитала равна

□ эластичность выпуска по затратам труда равна

□ эластичность выпуска по затратам труда равна .

12. Установите соответствие между названием модели и видом ее уравнения:

1. гипербола
2. парабола третьего порядка
3. многофакторная
4. линейная

2

3

1

4

13. Среди нелинейных эконометрических моделей рассматривают следующие

классы нелинейных уравнений: …

□ внешне линейные

□ внутреннее линейные

□ внешне нелинейные

□ внутренне нелинейные.

14. Укажите верные утверждения по поводу модели :

□ линеаризуется в линейную модель множественной регрессии

□ линеаризуется в линейную модель парной регрессии

□ относится к классу линейных моделей

□ относится к классу нелинейных моделей, но линейных по параметрам.

15. К классам нелинейных уравнений относятся:

□ уравнения, нелинейные относительно объясняющих переменных, но линейные по оцениваемым параметрам

□ лог-линейные уравнения

□ уравнения, нелинейные по оцениваемым параметрам

□ уравнения в частных производных.

Тема 5. Временные ряды

БЛОК 1

1. Пусть – временной ряд, – трендовая, – сезонная, а – случайная его составляющие. В принятых обозначениях мультипликативная временная модель выглядит следующим образом:

○ ,

○ ,

○ ,

○ .

2. Модели авторегрессии, модели скользящего среднего, смешанные модели авторегрессии-скользящего среднего относятся к

○ стационарным процессам второго порядка,

○ стационарным процессам первого порядка,

○ нестационарным процессам,

○ автокорреляционным функциям.

3. Модель временного ряда, имеющая следующую спецификацию (где – уровень временного ряда, – тренд, – сезонная компонента, – конъюнктурная компонента, – случайная компонента), называется …

○ нелинейной,

○ адаптивной,

○ мультипликативной,

○ смешанной.

4. Известны значения мультипликативной модели временного ряда: – значение уровня ряда, =15, Т – значение тренда, Т=5, S – значение сезонной компоненты, S=3, определите значение случайной компоненты Е.

○ Е=0,

○ Е=-1,

○ Е=1,

○ Е=3.

5. Как правило, в экономике основной причиной сезонных колебаний являются …

○ природно-климатические условия,

○ конъюнктурные колебания рынка,

○ неразвитая инфраструктура и недостаток финансирования,

○ человеческий фактор и административное управление.

13. Пусть – значения временного ряда с квартальными наблюдениями, – мультипликативная сезонная компонента, при чем для первого квартала года , для второго квартала года , для третьего квартала года . Определите оценку сезонной компоненты для четвертого квартала года

○ -3,

○ 3,

○ 1,

○ -1.

6. Экономические временные ряды, представляющие собой данные наблюдений за ряд лет, как правило, являются ……….. временными рядами.

○ строго убывающими,

○ строго возрастающими,

○ не зависящими от времени,

○ нестационарными.

7. Отличие наблюдений временного ряда от пространственной выборки состоит в том, что члены временного ряда не являются …

○ статистически независимыми и одинаково распределенными,

○ только одинаково распределенными,

○ распределенными по нормальному закону,

○ только статистически независимыми.

8. Пусть – значения временного ряда с квартальными наблюдениями, – мультипликативная сезонная компонента, при чем для второго квартала года , для третьего квартала года , для четвертого квартала года . Определите оценку сезонной компоненты для первого квартала года

○ 0,

○ 6/5,

○ -1,

○ 1.

9. Эргодичность временного ряда позволяет …

○ использовать выборочные аналоги генеральных характеристик временного ряда для определения его свойств,

○ анализировать свойства остатков временного ряда,

○ выделять сезонные колебания временного ряда,

○ использовать метод наименьших квадратов для аналитической записи тренда.

10. Под временным рядом (динамическим рядом или рядом динамики) понимается последовательность наблюдений некоторого признака Y, …

○ значения которого упорядочены во времени,

○ значения которого неупорядочены во времени,

○ который зависит от признака X, изменяющегося с течением времени,

○ который не изменяется с течением времени.

11. В стационарном временном ряде трендовая компонента …

○ отсутствует

○ имеет нелинейную зависимость от времени

○ имеет линейную зависимость от времени

○ присутствует.

12. Компонента временного ряда, отражающая повторяемость экономических процессов в течение не очень длительного периода (года, квартала, месяца и т.д.), называется …

○ случайной компонентой

○ циклической компонентой

○ трендом

○ сезонной компонентой.

13. Гипотеза о мультипликативной структурной схеме взаимодействия факторов, формирующих уровни временного ряда, означает …

○ сезонная компонента = уровень временного ряда уровень временного ряда конъюнктурная компонента случайная компонента

○ уровень временного ряда = тренд конъюнктурная компонента сезонный фактор случайная компонента

○ случайная компонента = тренд конъюнктурная компонента сезонный фактор уровень временного ряда

○ тренд = уровень временного ряда конъюнктурная компонента сезонный фактор случайная компонента.

14. Область значений автокорреляционной функции представляет собой промежуток …

○ [-1,0]

○ (-1,1)

○ [-1,1]

○ [0,1].

15. При моделировании временных рядов экономических показателей необходимо учитывать характер уровней исследуемых показателей …

○ конструктивный

○ стохастический

○ независящий от времени

○ аналитический.

32. Аддитивная модель содержит компоненты в виде …

○ слагаемых

○ отношений

○ комбинации слагаемых и сомножителей

○ сомножителей.

16. Пусть — стохастических процесс. Пусть для него выполнены следующие условия: — постоянство математического ожидания, — постоянство дисперсии, — автоковариация, зависящая только от величины лага между рассматриваемыми переменными. Тогда данный процесс является …

○ условно стационарным

○ совместно стационарным

○ нестационарным

○ слабо стационарным или стационарным в узком смысле.

17. Тенденция временного ряда характеризует совокупность факторов, …

○ оказывающих единовременное влияние

○ оказывающих долговременное влияние и формирующих общую динамику изучаемого показателя

○ не оказывающих влияние на уровень ряда

○ оказывающих сезонное воздействие.

18. К методам сглаживания уровней временного ряда относится вычисление …

○ темпов прироста уровней ряда

○ темпов роста уровней ряда

○ скользящей средней

○ последовательных сумм.

19. Стационарность временного ряда означает отсутствие …

○ наблюдений по уровням временного ряда,

○ значений уровней ряда,

○ временной характеристики,

○ тренда.

20. Временной ряд характеризует …

○ зависимость последовательных моментов (периодов) времени,

○ данные, описывающие один объект за ряд последовательных моментов (периодов) времени,

○ данные, описывающие совокупность различных объектов в определенный момент (период) времени,

○ совокупность последовательных моментов (периодов) времени.

21. Пусть – значения временного ряда с квартальными наблюдениями, – мультипликативная сезонная компонента, при чем для первого квартала года , для второго квартала года , для четвертого квартала года . Определите оценку сезонной компоненты для третьего квартала года

○ ,

○ 3/4,

○ 1,

○ -3/4.

22. «Белым шумом» называется …

○ регрессионный процесс,

○ неслучайный процесс,

○ чисто случайный процесс.

○ корреляционный процесс.

23. В общем случае каждый уровень временного ряда формируется под воздействием …

○ тенденции случайных факторов,

○ сезонных колебаний и случайных факторов,

○ случайных временных воздействий

○ тенденции, сезонных колебаний и случайных факторов.

24. Пусть – значения временного ряда с квартальными наблюдениями, – аддитивная сезонная компонента, при чем для первого квартала года , для второго квартала года , для третьего квартала года . Определите оценку сезонной компоненты для четвертого квартала года

○ -1,

○ 1/2,

○ 1/4,

○ 1.

25. В эконометрической практике стационарность временного ряда означает …

○ отсутствие случайной компоненты уровней тренда,

○ наличие сезонных колебаний,

○ наличие линейного тренда,

○ отсутствие строго периодических колебаний.

26. Для временного ряда численное значение в данный момент времени является отдельным наблюдением временного ряда и называется …

○ случайным возмущением,

○ уровнем ряда,

○ коэффициентом автокорреляции,

○ лагом для заданного наблюдения.

27. Пусть – значения временного ряда, – тренд-циклическая компонента этого ряда, – сезонная компонента, – случайная компонента. Тогда общий вид аддитивной модели временного ряда можно представить как …

○

○

○

○ .

28. Если случайные величины, образующие «белый шум», распределены нормально, тогда …

○ временной ряд имеет тренд,

○ для временного ряда ярко выражены сезонные колебания,

○ временной ряд является нестационарным,

○ этот временной ряд называется гауссовским белым шумом.

29. Пусть – значения временного ряда с квартальными наблюдениями, – мультипликативная сезонная компонента, при чем для первого квартала года , для второго квартала года , для четвертого квартала года . Определите оценку сезонной компоненты для третьего квартала года

○ 2,

○ 0,

○ 3/2,

○ 1/2.

30. Циклическая компонента имеет место во временных рядах, отражающих наблюдения в течение …

○ одного года,

○ длительного периода времени,

○ одного времени года (зима/весна/лето/осень)

○ периода меньше одного года.

БЛОК 2

1. Уровень временного ряда характеризуется конкретным значением …

□ экономического показателя в определенный момент времени,

□ сезонных колебаний временного ряда,

□ временного ряда в заданный момент (период) времени,

□ случайной компоненты временного ряда.

2. Укажите справедливые утверждения относительно автокорреляционной функции временного ряда.

□ служит для выявления структуры временного ряда,

□ служит для оценки случайной компоненты временного ряда,

□ представляет собой последовательность коэффициентов автокорреляции уровней временного ряда первого, второго и т.д. порядков,

□ является возрастающей функцией от уровней ряда.

3. Укажите группы факторов, формирующих уровень временного ряда:

□ временные факторы,

□ факторы, формирующие тенденцию ряда,

□ случайные факторы,

□ факторы, формирующие циклические колебания ряда.

4. Способами определения структуры временного ряда являются:

□ построение каррелограммы,

□ анализ автокорреляционной функции,

□ агрегирование данных за определенный промежуток времени,

□ расчет коэффициентов корреляции между объясняющими переменными.

5. Временным рядом является …

□ совокупность значений экономического показателя за несколько последовательных моментов (периодов) времени,

□ значения временных характеристик и соответствующие им значения экономического показателя,

□ совокупность временных факторов,

□ совокупность данных, описывающих различные объекты в определенный момент (период) времени.

6. Укажите эконометрические термины, которые относятся к моделям временных рядов:

□ (перекрестные данные) данные по однотипным объектам в разрезе n статистических наблюдений,

□ лаг,

□ автокорреляционная функция,

□ коррелограмма.

7. Выявление компонент тренда и сезонных колебаний проводится на основании …

□ построения и анализа коррелограммы,

□ исследования многофакторной модели,

□ моделирования систем эконометрических уравнений,

□ расчета и анализа коэффициентов автокорреляции различных порядков.

8. Установите соответствие между эконометрическими терминами и их определениями.

1. автокорреляция уровней временного ряда
2. коэффициент автокорреляции уровней временного ряда
3. автокорреляционная функция
4. коррелограмма.

4 график зависимости значений автокорреляционной функции от величины лага

1 корреляционная зависимость между последовательными уровнями ряда

2 коэффициент линейной корреляции между последовательными уровнями

3 последовательность коэффициентов автокорреляции первого, второго и т.д. порядков.

9. Методами выравнивания уровней временного ряда могут служить:

□ метод наименьших квадратов

□ графическое представление временного ряда

□ метод скользящей средней

□ построение уравнения регрессии, характеризующего зависимость уровней ряда от времени.

10. Укажите справедливые утверждения по поводу коэффициента автокорреляции уровней временного ряда:

□ равен коэффициенту линейной корреляции между последовательными уровнями исходного ряда

□ не может быть меньше 0

□ характеризует тесноту линейной связи между уровнями ряда

□ определяет вид временной модели (аддитивная или мультипликативная).

11. Пусть задан смешанный процесс авторегресси и скользящего среднего . Из приведенных ниже выберите уравнения и для проверки на стационарность и обратимость процесса соответственно.

□

□

□

□ .

12. Факторы, описывающие трендовую компоненту временного ряда, характеризуются …

□ периодическим воздействием на величину экономического показателя

□ долговременным воздействием на экономический показатель

□ случайным воздействием на уровень временного ряда

□ возможностью расчета значения компоненты с помощью аналитической функции от времени.

13. Построение модели временного ряда может быть осуществлено с использованием …

□ критерия Дарбина–Уотсона

□ мультипликативной модели

□ метода последовательных разностей

□ аддитивной модели.

14. Для выявления структуры временного ряда могут служить:

□ лаговая переменная

□ автокорреляционная функция

□ коэффициент детерминации

□ коррелограмма.

15. Способами определения структуры временного ряда являются:

□ построение коррелограммы

□ расчет коэффициентов корреляции между объясняющими переменными

□ агрегирование данных за определенный промежуток времени

□ анализ автокорреляционной функции.

16. Автокорреляционная функция характеризует …

□ зависимость значения коэффициента автокорреляции от его порядка,

□ значения коэффициентов автокорреляции, которые могут быть отображены на коррелограмме,

□ значения сезонной компоненты временного ряда,

□ уравнение тренда временного ряда.

17. Совокупность значений коэффициента автокорреляции, соответствующих порядкам, для которых они рассчитаны, может быть получена на основе …

□ модели временного ряда,

□ автокорреляционной функции,

□ значений факторов, которые формируют уровни временного ряда,

□ коррелограммы.