Лекция 3. Математические модели автоматических и автоматизированных систем.
Математические модели для исследования поведения системы и их адекватность
Для того, чтобы научится управлять СТС и изучить её свойства необходимо сначала получить и исследовать её математическую модель. Для этого необходимо описать в виде математических соотношений и уравнений все взаимосвязи между переменными характеризующими поведение объекта управления, управляющих устройств и других компонентов СТС. Исследование математической модели всегда предворяет реальное создание систем.
Математическая модель всегда представляет собой приближенное в той или иной степени описание, определяющее основные важные для данного исследования или использования системы свойства и поведение.
Есть понятие адекватности математической модели. Адекватная модель соответствует цели исследования по точности результатов и сложности описания системы.
В соответствии со сказанным, одной и той же СТС могут соответствовать различные модели в зависимости от потребной точности результатов исследования процессов управления.
Реальные технические системы, которые мы будем изучать, по своей природе являются динамическими. Для динамических систем можно назвать начальное состояние ,как совокупность некоторых величин, характеризующих ее состояние и имеется закон, по которому можно прогнозировать изменения этих величин с течением времени.
Непрерывные и дискретные во времени математические модели. Математические модели, основанные на дискретных событиях
Поведение реальных систем с механическими, электрическими, тепловыми процессами характеризуются инерционностью, которая описывается дифференциальными уравнениями .
Математические модели динамических систем можно классифицировать на:
1. непрерывные во времени математические модели, описываемые линейными или нелинейными дифференциальными уравнениями, выражающими баланс массы, энергии, сил и моментов.
2. дискретные во времени математические модели, описываемые разностными уравнениями линейными или не линейными.
Дискретным моделям соответствуют ситуации, когда информация в системе доступна для обработки только в определённые дискретные моменты времени. Эта ситуация характерна для цифровых систем управления, использующих в качестве устройства управления ЦВМ.
Определение периода дискретизации – важная задача возникающая при создании таких систем.
3.модели систем, основанные на дискретных событиях. Многие системы можно рассматривать как системы очередей и моделировать динамику их поведения событиями прихода в очередь заявок на обслуживание и обслуживанию заявок из очереди.
Все эти типы моделей, описывающих СУ, находятся под воздействием случайных или неопределённых возмущений и случайных или неопределённых отклонений параметров от их номинальных значений. Эти случайные возмущения и отклонения параметров являются либо следствием неполноты знаний, либо физических процессов – шумов, которые можно описать статистически.
При составлении математических моделей всех типов, существует два подхода:
1. физический подход, когда составляются уравнения модели на основе физических законов и отношений баланса энергии, сил, массы.
2. подход, основанный на проведении эксперимента, в процессе которого определяются (идентифицируются) параметры и характеристики соответствующих моделей.
На практике чаще всего применяются комбинации методов, когда составленные на базе физических соотношений уравнения уточняются (структура и параметры) на базе экспериментальных данных, полученных на базе опытов над физическими моделями или аналогичными системами.
Математические модели мехатронных систем
Мехатронные системы – термин, введенный для широкого класса систем автоматического управления, в которых механические объекты управляются от компьютеров. Например, самолеты, автомобили, ракеты, роботы, станки, двигатели, турбины, антенны с наведением и т.п. составление и преобразования математической моделей рассмотрим на примере данного популярного класса систем автоматизации и управления.
Краеугольным камнем для динамической модели мехатронной системы является второй закон Ньютона. Для применения второго закона Ньютона необходимо задать некоторую систему координат, относительно которой будет определяться скорость, положение, направление сил, действующих на объект.
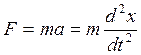 , F- вектор сил
, F- вектор сил 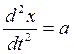 , а - вектор ускорения, m – масса объекта.
, а - вектор ускорения, m – масса объекта.
Если проинтегрировать это уравнение при нулевых начальных условиях, то
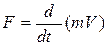 , где
, где 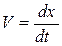 или
или
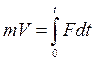 =Ft
=Ft
Импульс силы равен изменению количества движения. Именно так сформулировал свой закон Ньютон.
Иногда второй закон Ньютона записывается в виде системы уравнений первого порядка относительно координат «состояния системы»:
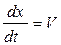 ,
, 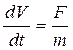
Подобная запись принята стандартной для описания динамики системы в «переменных состояний системы», за которые мы принимаем x и V. Математик сказал бы , что дифференциальное уравнение записано в форме Коши – в виде системы дифференциальных уравнений первого порядка , разрешенных относительно первой производной
Закон Ньютона для вращающихся тел имеет вид
J 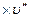 =М
=М 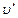 =
= 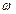
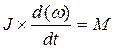
, где М – момент сил относительно центра вращения,
ω – угловая скорость тела ,
J – момент инерции.
Подобными уравнениями описываются вращение или колебания самолетов , ракет, относительно их центров масс.
Если ввести понятие угла поворота тела 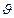 , то запись состояний системы имеет вид
, то запись состояний системы имеет вид
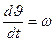 ,
, 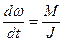
Эта система уравнений описывает динамику вращения в переменных состояния 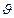 и
и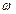 . Состояние – набор всех переменных, первые производные которых входят в описание динамики системы.
. Состояние – набор всех переменных, первые производные которых входят в описание динамики системы.
Линейные системы, нелинейные системы, их линеаризация
В природе нелинейные системы встречаются чаще, чем линейные. С другой стороны исследование линейных систем проще, чем нелинейных. Это происходит в основном за счет того, что для линейных систем справедливы два замечательных свойства:
Однородности и аддитивности.
Свойство однородности означает , что изменение в к раз величины входного воздействия (сигнала) приводит к аналогичному в к раз величины выходного сигнала.
Свойство аддитивности можно сформулировать так:
Для любых входных сигналов x1(n) и x2(n), которым соответствуют выходные сигналы y1(n) и y2(n), справедливо, что входному сигналу ( x1(n)+x2(n)) соответствует выходной сигнал (y1(n)+y2(n)).
Иногда это свойство излогается как принцип суперпозиции:
