Численные методы математического программирования
Большинство задач оптимизации в конечном счете сводятся (либо косвенно, либо непосредственно) к той или иной задаче математического программирования. Поэтому очень важно владеть методами решения такого рода задач. В достаточно общем виде эта задача формулируется как задача поиска такого n-мерного вектора х* из допустимого множества X, который обращает целевую (критериальную) функцию f(x) в минимум
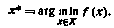
Ниже описываются лишь наиболее распространенные методы численного решения задач математического программирования.
Методы безусловной оптимизации. К задачам безусловной оптимизации относят задачи, в которых ограничения на искомый вектор отсутствуют. Задача состоит в поиске вектора х* из условия обращения функции f(x) в минимум
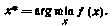
Градиентные методы.Сущность методов этой группы заключается в том, что каждое новое (k+1)-e приближение хk+1 вектора х к минимуму функции f(x) формируется на основе текущего k-го приближения хk по схеме
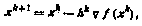
где через hk обозначена величина шага поиска в направлении антиградиента — 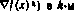 в k-м приближении. Наибольшее распространение получили следующие разновидности градиентных методов:
в k-м приближении. Наибольшее распространение получили следующие разновидности градиентных методов:
Метод градиентного спуска, предполагающий задание шага поиска hk в каждом приближении достаточно малым. Основное свойство метода состоит в том, что траектория градиентного спуска ортогональна всем линиям уровня минимизируемой функции f(x)= const.
Градиентный метод с использованием «большого» шага поиска (по крайней мере, по сравнению с методом градиентного спуска). Так как использование поcтоянного «большого» шага поиска hk = const может привести к расходимости процесса поиска, то, как правило, используют дробление шага.
Метод наискорейшего спуска, предполагающий использование в каждом приближении наилучшего шага поиска. Наилучший шаг поиска hk определяется из условия достижения минимизирующей функцией f(x) минимума в направлении антиградиента — 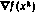 :
:
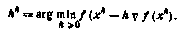
Методы второго порядка и их модификации. Основной недостаток градиентных методов состоит в слабой скорости сходимости к искомому минимуму, особенно при проявлении так называемого «эффекта овражности». Это объясняется тем, что по сути градиентные методы используют линейную аппроксимацию минимизирующей функции f(x). В отличие от последних методы второго порядка базируются на использовании квадратичной аппроксимации функции f(x). За счет этого удается повысить скорость сходимости особенно вблизи экстремума.
Одним из основных методов второго порядка является метод Ньютона, сущность которого состоит в отыскании на каждой итерации минимума квадратичной аппроксимации. В результате получаем следующий алгоритм:
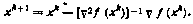
Здесь через 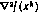 обозначен гессиан, т. е. матрица вторых частных производных функции f(x) в точке xk. Предполагается, что матрица
обозначен гессиан, т. е. матрица вторых частных производных функции f(x) в точке xk. Предполагается, что матрица 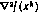 является положительно определенной.
является положительно определенной.
Существуют различные модификации метода Ньютона, призванные, с одной стороны, улучшить сходимость метода независимо от начального приближения и независимо от свойств минимизирующей функции, а с другой, упростить сам алгоритм поиска. Приведем здесь лишь некоторые.
Метод Ньютона с регулировкой шага поиска
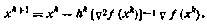
Шаг поиска hk, как и в градиентных методах, может выбираться различными способами. Один из них состоит в выборе наилучшего шага в выбранном направлении поиска:
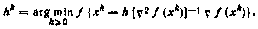
Упрощенный метод Ньютона
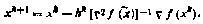
В данной модификации гессиан 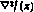 предполагается для упрощения вычислять не на каждой итерации, а один раз в некоторой заранее выбранной точке
предполагается для упрощения вычислять не на каждой итерации, а один раз в некоторой заранее выбранной точке 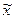 .
.
Комбинированный метод Ньютона.
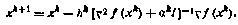
Здесь I — единичная матрица, ak —некоторый дополнительный параметр на k-й итерации. Параметр ak и шаг поиска hk подбираются эмпирически так, чтобы метод вдали от минимума был бы близок к градиентному, а по мере приближения к минимуму переходил в обычный метод Ньютона. Метод применим и в случае, когда гессион функции f(x) не является положительно-определенным.
Квазиньютоновские методы. Это — целая группа методов, в которых вместо матрицы 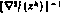 на k-R итерации используются различные ее аппроксимации Hk. Общая схема методов имеет вид
на k-R итерации используются различные ее аппроксимации Hk. Общая схема методов имеет вид
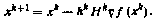
Преимущество методов состоит в отсутствии операции обращения. Приведем лишь один из многочисленных алгоритмов формирования матриц Hk — алгоритм Давидона — Флетчера — Пауэлла:
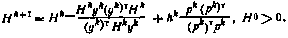
Здесь использованы обозначения
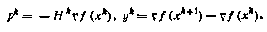
Метод сопряженных градиентов относится к числу многошаговых методов, которые на каждой итерации используют не только текущую информацию на предыдущих шагах поиска, т. е. учитывают предысторию процесса поиска. Схема метода сопряженных градиентов такова:
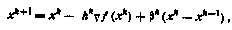
где hk, Bk — параметры, подбираемые на каждой итерации.
Существуют различные алгоритмы реализации метода. Наиболее распространенный алгоритм Флетчера — Ривса имеет вид
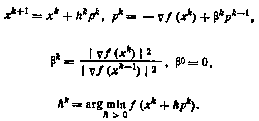
Методы условной оптимизации. К задачам условной оптимизации принято относить задачи, в которых на искомый вектор х* накладываются дополнительные ограничения. В общем случае, как уже указывалось, задача имеет вид
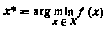
Наиболее распространенным методом решения такого рода задач является метод штрафных функций. Сущность его состоит в построении такой последовательности задач безусловной оптимизации, чтобы последовательность, составленная из их решений 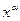 , стягивалась к решению исходной задачи х* (например, при
, стягивалась к решению исходной задачи х* (например, при 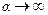 ). Для этого достаточно ввести функцию штрафов
). Для этого достаточно ввести функцию штрафов 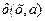 , такую, чтобы
, такую, чтобы
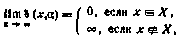
и рассмотреть следующую задачу безусловной оптимизации
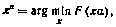
где 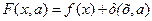 .
.
Очевидно, 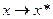 при
при 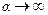 . При
. При 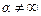 , но большом, получим приближенное решение исходной задачи.
, но большом, получим приближенное решение исходной задачи.
В зависимости от способа формирования функции штрафов различают следующие методы штрафных функций.
Метод внутренней точки предполагает построение штрафов таким образом, чтобы при приближении вектора 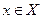 к границе области X величина
к границе области X величина 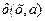 неограниченно возрастала. В этом случае траектория поиска минимума (если, конечно, поиск начат с внутренней точки множества X) полностью будет лежать внутри множества X. Отсюда и название метода.
неограниченно возрастала. В этом случае траектория поиска минимума (если, конечно, поиск начат с внутренней точки множества X) полностью будет лежать внутри множества X. Отсюда и название метода.
Если рассматривается задача минимизации функции f(x) при ограничениях 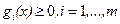 , то в качестве штрафов могут быть использованы, например, такие функции:
, то в качестве штрафов могут быть использованы, например, такие функции:
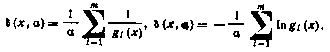
Основные достоинства метода внутренней точки заключаются в следующем. В процессе поиска целевая функция уменьшается без нарушения ограничений. Поэтому нет необходимости отдельно учитывать границу допустимой области (например, пытаться двигаться по границе). Преобразованная целевая функция F(x, а) сохраняет в общем свойства исходных функций f(x) и 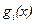 (например непрерывность, дифференцируемость). К недостаткам метода следует отнести необходимость иметь в качестве начальной точки поиска допустимую точку, а также неприменимость метода при наличии ограничений типа равенств.
(например непрерывность, дифференцируемость). К недостаткам метода следует отнести необходимость иметь в качестве начальной точки поиска допустимую точку, а также неприменимость метода при наличии ограничений типа равенств.
Метод внешней точки предполагает построение штрафов таким образом, чтобы значения преобразованной функции F(x, а) в допустимой области точно или приближенно равнялись значениям исходной целевой функции f(x), а вне допустимой области существенно превосходили значения f(x). Для задачи отыскания min f(x) при ограничениях 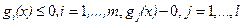 , наиболее распространены следующие функции штрафов:
, наиболее распространены следующие функции штрафов:
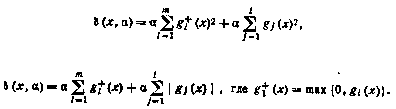
Преимущества метода внешней точки заключаются в большей его универсальности: метод применим при наличии различных ограничений (равенств и неравенств), процесс поиска может быть начат из любой точки (допустимой и недопустимой). К недостаткам метода следует отнести тот факт, что элементы последовательности 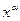 при
при 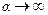 не принадлежат допустимой области, а также невозможность при некоторых функциях штрафа применения методов поиска с использованием вторых производных.
не принадлежат допустимой области, а также невозможность при некоторых функциях штрафа применения методов поиска с использованием вторых производных.
Учитывая сказанное, на практике может оказаться наиболее эффективным применение комбинированного метода штрафных функций: для части ограничений (типа неравенств) применяется метод внутренней точки, а для другой части ограничений (типа равенств) — метод внешней точки. Преобразованная целевая функция в этом случае может быть представлена, например, в виде
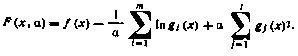
СПИСОК ЛИТЕРАТУРЫ
1. Аоки М. Оптимизация стохастических систем. М: Наука, 1971, 350 с.
2. Барра Ж. Р. Основные понятия математической статистики. М.: Мир, 1974. 275 с.
3. Батков А. М., Тарханов И. М. Системы телеуправления. М.: Машиностроение, 1972. 192 с.
4. Брайсон, Хл-Ю-ши. Прикладная теория оптимального управления. М.: Мир, 1972.
5. Богуславский И.А. Методы навигации и управления по неполной статистической информации. М.: Машиностроение, 1970. 256 с.
6. Брандин В.Н., Васильев А.А., Худяков С.Т. Основы экспериментальной космической баллистики. М.: Машиностроение, 1974. 339 с.
7. Бусленко Н.П., Шрейдер Ю.А. Метод статистических испытаний. «Метод Монте-Карло». М.: Физматгиз, 1962. 332 с.
8. Вентцель Е.С. Теория вероятностей. М.: Физматгиз, 1969, 564 с.
9. Гихман И.И., Скороход А.В. Стохастические дифференциальные уравнения. Киев: Наукова думка, 1968. 353 с.
10. Доброленский К.П. Динамика полета в неспокойной атмосфере. М.: Машиностроение, 1969. 256 с.
11. Закс Ш. Теория статистических выводов. М.: Мир, 1975. 776 с.
12. Зангвилл У.И. Нелинейное программирование. М.: Сов. радио, 1973. 312 с.
13. Казаков И.Е. Статистическая теория систем управления в пространстве состояний. М.: Наука, 1975. 432 с.
14. Крамер Г. Математические методы статистики. М.: Мир, 1975. 648 с.
15. Красовский А.А. Статистическая теория переходных процессов в системах управления. М.: Наука, 1968. 240 с.
16. Бажинов И.К., Почукаев В.Н., Поляков В.С. Космическая навигация. М.: Машиностроение: 1975. 352 с.
17. Космические траекторные измерения/Под ред. П.А. Агаджанова и др. М.: Сов. радио, 19*69. 498 с.
18. Корн Г.А. Моделирование случайных процессов на аналоговых и аналого-цифровых машинах. М.: Мир, 1968. 315 с.
19. Лебедев А.А., Красильщиков М.Н.,Малышев В.В. Оптимальное управление движением космических летательных аппаратов. М.: Машиностроение, 1974. 200 с.
20. Лебедев А.А., Чернобровкин Л.С. Динамика полета беспилотных летательных аппаратов. М.: Машиностроение, 1973. 616 с.
21. Лебедев А.А., Карабанов В.А. Динамика систем управления беспилотными летательными аппаратами М.: Машиностроение, 1965. 528 с.
22. Лебедев А.А., Герасюта Н.Ф. Баллистика ракет. М.: Машиностроение, 1970. 244 с.
23. Летов А. М. Динамика полета и управление. М.: Наука, 1969. 360 с.
24. Лившиц Н.А., Виноградов В.Н., Голубев Г.А. Корреляционная теория оптимального управления многомерными процессами. М.: Сов. радио, 1974. 328 с.
25. Лэннинг Д.X., Бэттин Р. Г. Случайные процессы в задачах автоматического управления. М.: ИЛ, 1958. 387 с.
26. Методы оптимизации в статистических задачах управления/А. М. Б а т-ков и др. — М.: Машиностроение, 1974. 240 с.
27. Митропольский А.К. Техника статистических вычислений. М.: Наука, 1971. 576 с.
28. Моисеев Н.Н., Иванилов Ю.П., Столярова Е.М. Методы оптимизации. М.: Наука, 1978. 352 с.
29. Основы теории полета космических аппаратов. Под ред. Г.С. Нариманова, М.К. Тихонравова. М.: Машиностроение, 1972. 607 с.
30. Острей К. Введение в стохастическую теорию управления. М.: Мир, 1973. 322 с.
31. Пропой А.И. Элементы оптимальных дискретных процессов. М.: Наука, 1973. 256 с.
32. Пугачев В.С. Теория случайных функций и ее применение к задачам автоматического управления. М.: Физматгиз, 1962. 883 с.
33. Росин М.Ф. Статистическая динамика и теория эффективности систем управления. М.: Машиностроение, 1970. 335 с.
34. Статистическая динамика управляемого полета. А.А. Лебедев, В.Т. Бобронников, М.И. Красильщиков, В.В. Малышев.М.: Машиностроение, 1978. 200 с.
35. Фельдбаум А.А. Основы теории оптимальных автоматических систем. М.: Наука, 1966. 624 с.
36. Черноусым Ф.Л., Колмановский В.Б. Оптимальное управление при случайных возмущениях. М.: Наука, 1978. 351 с.
37. Эльясберг П.Е. Определение движения по результатам измерений. — М.: Наука, 1976.— 416 с.
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Алгоритм оценивания:
— — байесовский 66
— — максимума правдоподобия 135
— — наименьших квадратов 116
Б
Белый шум 22, 25
Д
Детерминированная система 148, 173
Динамическое программирование 188
Дисперсия случайной величины 10
Достаточные условия оптимальности ф 188, 229
К
Каноническое разложение 23 Корреляционный момент 11 Корреляционная функция 20
Л
Линейное преобразование случайной величины 13
М
Математическое ожидание 9, 19
Метод Монте-Карло 55
Метод статистической линеаризации
Н
Нелинейное преобразование случайной величины 13
Необходимые условия оптимальности
О
Однопараметрическая коррекция 214
Оценка:
— байесовская 64
— максимума апостериорной вероятности 64
— максимума правдоподобия 64
— несмещенная 63
— оптимальная 63
— состоятельная 62
Оценка точности:
— — априорная 130
— — — аналитическая 130
П
Переходная матрица 33
Плотность вероятности случайной величины 7
Принцип минимума (максимума) 150, 168, 172
Программирование оптимального управления 141
Производная по направлению 144
Р
Риск:
— средний 63
— условный 64
— байесовский 64
Семиинвариант 15
Синтез управления 141, 188:
— — при неполной информации 243
Случайный процесс 16:
— — марковский 18
Случайная величина 7
Случайное поле 26:
— — скалярное 26
— — векторное 28
Сопряженный стохастический вектор 147
Спектральная плотность 24
Стохастическая система 142:
— — дискретная 142
— — линейная 174, 191
— — непрерывная 169
Стохастическое дифференциальное уравнение 47
Стохастическое уравнение Беллмана 229
Стохастический гамильтониан 146
Т
Турбулентность атмосферы 30
Ф
Фильтр:
— второго порядка 109
— Калмана дискретный 66
— — непрерывный 67
— — квазилинейный 93
Формирующий фильтр 40
Формула Байеса 9, 65
Функция потерь 63
Х
Характеристическая функция 15
Ч
Частотная характеристика 37
Частотный метод анализа точности 36
Численные методы программирования 158:
— — — градиентные 158
— — — второго порядка 163
Э
Эргодическое свойство 21
ОГЛАВЛЕНИЕ
Предисловие
Введение
Глава 1. Методы статистического описания случайных величин, процессов и полей
1.1. Случайные величины
1.1.1. Скалярные и векторные случайные величины
1.1.2. Моменты случайных величин
1.1.3. Нормальное распределение
1.1.4. Линейные и нелинейные преобразования случайных величин
1.1.5. Характеристическая функция и семиинварианты
1.2. Случайные процессы
1.2.1. Определение и классификация случайных процессов
1.2.2. Корреляционная теория случайных процессов
1.2.3. Каноническое разложение случайных процессов
1.2.4. Спектральная плотность
1.3. Случайные поля
1.3.1. Скалярные случайные поля
1.3.2. Векторные случайные поля
1.3.3. Статистическое описание турбулентности атмосферы как векторного случайного поля
Глава 2. Методы априорного статистического анализа управляемого движения летательных аппаратов
2.1. Метод переходной матрицы
2.2. Частотный метод
2.3. Формирующие фильтры
2.4. Метод статистической линеаризации
2.5. Методы теории марковских процессов
2.6. Метод статистического моделирования (Монте-Карло)
Глава 3. Методы определения оценок состояния летательных, аппаратов
3.1. Задача оценивания как частный случай статистического решения. Основные понятия и определения
3.2. Байесовские алгоритмы оценивания
3.2.1. Фильтр Калмана — линейный байесовский алгоритм оценивания
3.2.2. Определение орбиты стационарного искусственного спутника Земли (СИСЗ) по данным наземных радиолокационных измерений с использованием фильтра Калмана
3.2.3. Применение фильтра Калмана для начальной выставки инерциальной навигационной системы беспилотного летательного аппарата
3.2.4. Квазилинейный дискретный фильтр Калмана
3.2.5. Определение состояния спускаемого аппарата по данным автономных измерений с использованием квазилинейного фильтра Калмана
3.2.6. Фильтр второго порядка
3.2.7. Применение фильтра второго порядка для определения орбиты стационарного ИСЗ по данным автономных навигационных средств
3.3. Метод наименьших квадратов
3.3.1. Классическая форма метода наименьших квадратов
3.3.2. Рекуррентная форма метода наименьших квадратов
3.3.3. Определение орбиты искусственного спутника Земли с использованием метода наименьших квадратов
3.3.4. Аналитический алгоритм априорной оценки точности с использованием метода наименьших квадратов
3.4. Метод максимума правдоподобия
3.4.1. Метод максимума правдоподобия при нормальном распределении ошибок измерений
Глава 4. Программирование оптимального управления летательными аппаратами
4.1. Постановка задачи. Случай дискретного времени
4.2. Необходимые условия оптимальности
4.3. Оптимизация процесса коррекции космического аппарата
4.4. Численные методы программирования оптимального управления
4.5. Необходимые условия оптимальности для непрерывного случая. Непрерывный принцип минимума (максимума)
4.6. Оптимальное управление летательным аппаратом в бессиловом поле. Оптимальное управление линейной системой
4.7. Задача оптимального планирования навигационных измерений
Глава 5. Синтез оптимального управления летательными аппаратами
5.1. Достаточные условия оптимальности. Метод динамического программирования
5.2. Оптимальное управление линейной стохастической системой
5.3. Учет изопериметрических ограничений
5.4. Оптимальное управление стационарным спутником с использованием импульсной корректирующей двигательной установки
5.5. Методы приближенного синтеза оптимального управления
5.6. Оптимизация процесса коррекции траектории космического аппарата
5.7. Оптимизация процесса перевода стационарного ИСЗ в заданное положение с использованием двигательной установки малой тяги
5.8. Достаточные условия оптимальности в непрерывном случае. Стохастическое уравнение Беллмана
5.9. Оптимальное управление сближением летательных аппаратов. Линейные непрерывные системы, оптимизируемые по квадратичному критерию
5.10. Оптимальное управление конечным состоянием спускаемого аппарата
5.11. Учет изопериметрических ограничений
5.12. О методах приближенного синтеза оптимального управления в непрерывном случае
Глава 6. Оптимальное управление летательными аппаратами при неполной информации
6.1. Оптимальное дискретное управление при неполной информации. Достаточные координаты
6.2. Оптимальное управление линейной дискретной системой при аддитивных возмущениях и квадратичном критерии оптимальности
6.3. Оптимальное управление линейной непрерывной системой при наличии аддитивных возмущений
6.4. Синтез автономной системы управления спускаемым аппаратом
6.5. Минимаксные (игровые) задачи синтеза. Достаточные условия оптимальности
6.6. Гарантирующая стратегия управления при однопарамет-рической коррекции летательного аппарата
6.7. Алгоритм гарантированного управления квадратичным конечным состоянием летательного аппарата
Приложения
1. Значения функции Лапласа
2. Формулы для вычисления стандартного интеграла
3. Формулы для статистических коэффициентов усиления типовых нелинейных звеньев
4. Векторное дифференцирование
5. Два способа описания линейных динамических систем
6. Численные методы математического программирования
Список литературы
Предметный указатель
Александр Александрович Лебедев, Владимир Тимофеевич Бобронников, Михаил Наумович Красильщиков, Вениамин Васильевич Малышев
СТАТИСТИЧЕСКАЯ ДИНАМИКА И ОПТИМИЗАЦИЯ УПРАВЛЕНИЯ ЛЕТАТЕЛЬНЫХ АППАРАТОВ
Редактор И. А. Суворова
Художественный редактор В. В. Лебедев
Переплет художника А. Н. Ковалева
Технический редактор Т. И. Андреева
Корректоры И. М. Борейша и Л. Я. Шабашова
ИБ № 4502
Сдано в набор 23.10.84.
Подписано в печать 13.03.85 Т-08105.
Формат 60×901/18. Бумага типографская № 1.
Печать высокая. Гарнитура литературная.
Усл. печ. л. 17,5. Усл. кр.-отт. 17,5. Уч.-изд. л. 18,20.
Тираж 3 400 экз. Заказ 968. Цена 1 руб.
Ордена Трудового Красного Знамени издательство «Машиностроение», 107076, Москва, Стромынский пер., 4.
Московская типография № 8 Союзполиграфпрома при Государственном комитете СССР по делам издательств, полиграфии и книжной торговли, 101898, Москва, Центр, Хохловский пер., 7.
