Методы приближенного синтеза оптимального управления

Основной трудностью на пути применения достаточных условий оптимальности при решении задач синтеза является так на­зываемое «проклятие размерности», заключающееся в необходимо­сти запоминания на каждом шаге оптимизации функции будущих потерь, являющейся в общем случае функцией п переменных. Запо­минание таких функций при больших п (начиная с п =3) требует огромного объема памяти и оказывается непосильной задачей даже для современных ЦВМ. В связи с этим приходится прибегать к раз­личным приближенным методам, основанным либо на линеаризации (обычной и статистической), либо на аппроксимации функции буду­щих потерь. В последнем случае наличие ограничений, накладывае­мых на вектор управления и на вектор фазовых координат, может существенно облегчить решение задачи синтеза.

Метод линеаризации. Рассмотрим задачу синтеза оптимально­го управления системой

из условия обращения в минимум критерия

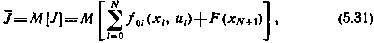
полагая сначала, что ограничения на вектор управления отсутст­вуют, а векторы 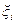образуют «белую» последовательность с корре­ляционными матрицами 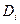. Предположим, что возмущенное дви­жение системы (5.30) может быть описано уравнениями в откло­нениях

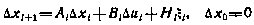
относительно некоторой программной траектории, определяемой уравнением

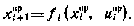
Здесь введены обозначения:

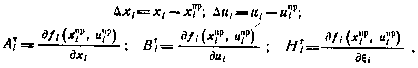
Разложим выражение (5.31) для критерия оптимальности в ряд Тейлора с точностью до членов второго порядка малости

Где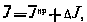

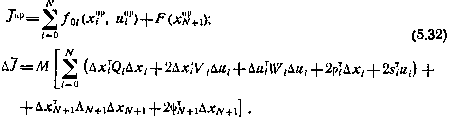
Так как 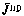зависит только от программной составляющей управ­ления 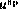, то для выбора последовательности 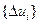следует мини­мизировать 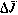. С этой целью обратимся к основному рекуррентно­му соотношению метода динамического программирования. Как и прежде, можно показать, что функция будущих потерь при неко­торых предположениях может быть представлена в виде

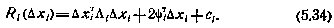
Действительно, для момента i=N+1 соотношение (5.34) имеет мес­то, причем

Предположим теперь, что (5.34) имеет место для (i+1)-го мо­мента, т. е.

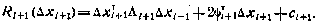
Тогда на основании рекуррентного соотношения (5.28) получим

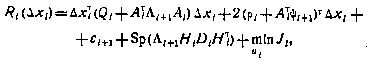
где

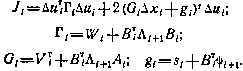
Полагая, что матрица 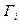— положительно определенная, находим

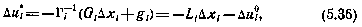
Где

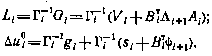
С учетом найденного управления выражение для функции 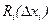принимает вид (5.34). При этом

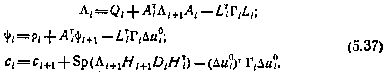
Применяя рекуррентные соотношения (5.37) при граничных условиях (5.35), можно последовательно определить все коэффи­циенты обратной связи 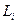и систематические составляющие 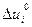в законе (5.36). Значение функции будущих потерь в момент i = 0 определит минимальное значение .

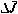Так как по условию 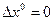, то получаем

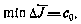
До сих пор предполагалось, что программная траектория 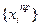известна. Поэтому матрицы 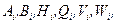Λ_N+1 и век­торы 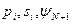считались также известными.

Нетрудно заметить, что величина 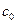, определяющая минималь­ное значение составляющей ΔJ и зависящая от указанных матриц, оказывается в конечном счете зависящей от программной траектории. Стремясь в конечном счете к достижению минимума полного критерия 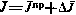, выбор программной траектории следует Те­перь подчинить условию

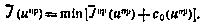
Здесь под 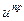понимается последовательность управлений 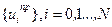, определяющая программную траекторию.

Метод статистической линеаризации. Рассмотренный выше ме­тод применим в случаях, когда на вектор управления не наклады­ваются ограничения. Однако он может быть распространен и на случай ограниченного управляющего воздействия, если воспользо­ваться дополнительно методом статистической линеаризации.

Обратимся снова к задаче синтеза оптимального управления системой (5.30) из условия обращения в минимум критерия (5.31). Однако будем теперь считать, что на вектор управления 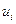накла­дываются ограничения 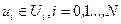. Для простоты считаем, что множество 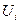представляет собой m-мерный параллелепипед

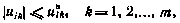
где 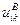— заданное значение.

Как и раньше, через 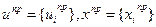обозначим програм­мное управление, удовлетворяющее теперь ограничениям, и соответ­ствующую траекторию движения (без учета возмущения).

Уравнения в отклонениях и выражение для приращения крите­рия оптимальности имеет прежний вид. Однако задачу минимиза­ции составляющей 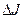теперь не удается решить так просто, ибо не­обходимо учитывать ограничения 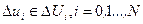, где мно­жества 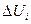определяются неравенствами

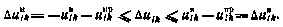
В силу этих ограничений закон оптимального управления 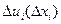теперь уже не будет линейным. Однако, производя статис­тическую линеаризацию зависимости 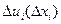в каждый момент времени, можно показать, что функция будущих потерь по-прежне­му имеет вид (5.34):

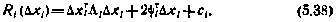
Действительно, для момента i=N+1 соотношение это имеет мес­то. Полагая далее, что оно справедливо и для (i+1)-гo момента, получаем

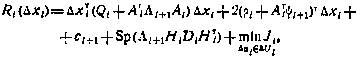
Где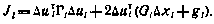

Здесь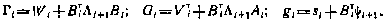

Тогда, осуществляя минимизацию по 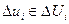получим следующий закон управления:

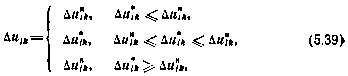
где через 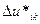обозначены компоненты вектора, определяемого со­гласно (5.36):

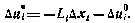
Здесь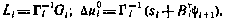

По-прежнему предполагается положительная определенность мат­рицы .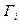

Произведем статистическую линеаризацию зависимости (5.39), т. е. заменим ее следующей:

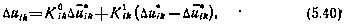
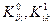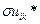где — коэффициенты статистической линеаризации зави­сящие от математического ожидания и среднеквадратичного отклонения величины .

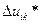Введем в рассмотрение диагональные матрицы 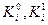с эле­ментами 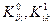соответственно. Тогда соотношения (5.40) могут быть переписаны в виде

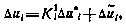
Где

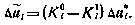
Так как 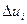линейно по 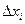, то, как и прежде, получаем для 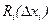выражение в виде (5.38), причем

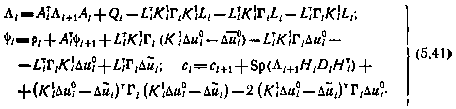
Граничные условия для этих рекуррентных соотношений по-прежнему имеют вид (5.35). Чтобы воспользоваться этими соотно­шениями, необходимо знать математические ожидания и среднеквадратичные отклонения компонент вектора 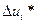,так как послед­ние определяют матрицы 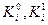. С этой целью обратимся к урав­нениям для математического ожидания 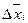и корреляционной матрицы вектора 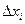. Эти уравнения могут быть представлены в следующем виде:

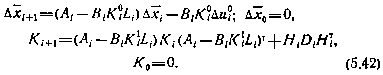
При этом

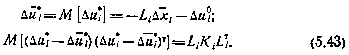
Так как система (5.41) имеет граничные условия на правом конце, а система (5.42) — на левом, то имеем краевую задачу. Ее решение может быть получено с помощью методов последователь­ных приближений. Один из простейших методов может состоять в следующем:

1. Задается начальное приближение матрицы .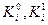

2. Определяется алгоритм субоптимального управления (точ­нее, его параметры 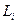, 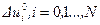) согласно (5.39) — (5.41).

3. Производится уточнение матрицы 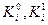на основе статисти­ческих характеристик (5.43), полученных в соответствии с (5.42) при найденном алгоритме управления.

В качестве начального приближения матриц 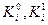можно ре­комендовать единичные матрицы. Нетрудно заметить, что при этом начальное приближение будет соответствовать случаю неограничен­ного управления.

Для иллюстрации метода рассмотрим задачу одноимпульсной однопараметрической коррекции. Математическая модель в этом случае может быть записана в виде

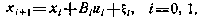
Предположим, что 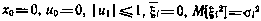. Крите­рий оптимальности имеет вид 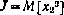. Применение достаточных условий оптимальности в данном случае позволяет найти точное ре­шение задачи. Алгоритм коррекции имеет следующий вид:

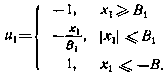
Функция будущих потерь 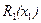равна

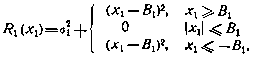
Величина критерия оптимальности при этом вычисляется по фор­муле

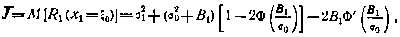
где через Ф, Ф' обозначены интеграл вероятностей и его производ­ная [32].

Обратимся теперь к методу статистической линеаризации. Про­изводя статистическую линеаризацию найденного алгоритма кор­рекции, получаем

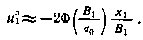
Вычисляя величину критерия оптимальности при данном управле­нии, будем иметь

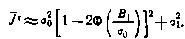
Сравнивая выражения для оценок , можно установить, что максимально возможная ошибка оценки достигается при 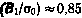и составляет ~6% от величины .

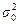Таким образом, использование метода статистической линеари­зации совместно с методом динамического программирования поз­воляет получить приближенное решение задачи синтеза.

Область применения предложенного метода не ограничивается рассмотренным случаем. Метод может быть применен и в более об­щих случаях, например, когда вектор-функция правых частей урав­нений не является дифференцируемой функцией или когда линеари­зованная обычным способом система не описывает точно возмущен­ное движение исходной системы. В этих случаях по-прежнему можно прийти к линеаризованной системе, однако путем ее стати­стической линеаризации.

Метод параметров. Сущность метода параметров состоит в отыс­кании наилучших в том или ином смысле значений параметров и разложении функции будущих потерь с помощью использования ос­новного рекуррентного соотношения метода динамического програм­мирования. Ниже рассматриваются две модификации метода па­раметров применительно к задаче синтеза оптимального управле­ния системой

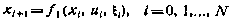
из условия минимума критерия

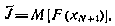
1. Аппроксимация функции потерь полиномами. Предположим, что функции f_i, F являются непрерывно-дифференцируемыми, а уп­равление 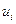неограниченным. Для простоты будем считать 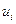скаля­ром. Представим функцию будущих потерь 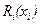в виде разло­жения

где 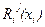—однородная форма степени j. Так,

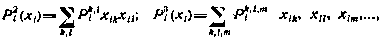
причем

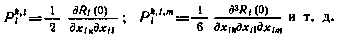
Подставляя оценку 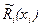в основное рекуррентное соотношение метода динамического программирования, получаем

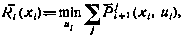
где

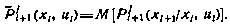
Для осуществления операции минимизации по управлению мож­но воспользоваться методом Ньютона, согласно которому

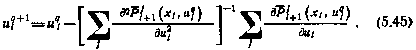
Предполагается, конечно, что метод сходится. С целью сокращения числа итераций начальное приближение 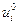целесообразно задавать исходя из физических соображений. Если это трудно сделать, мож­но положить .

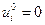Функция будущих потерь на q-й итерации тогда может быть представлена в виде

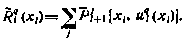
Приравнивая в левой и правой частях этого выражения коэффи­циенты при одинаковых степенях можно получить следующие ре­куррентные соотношения для определения коэффициентов в одно­родных формах:

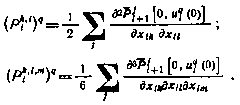
Нетрудно установить, что применение данного метода к задаче управления линейной системой с квадратичным критерием опти­мальности позволяет за одну итерацию получить точное решение задачи. В случае нелинейных систем метод может быть использован для получения приближенного решения задачи.

Метод наиболее удобен в случае полиномиальных функций 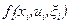. Пусть, например, система описывается одномерным уравнением

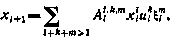
а критерий оптимальности имеет вид

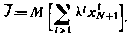
В этом случае

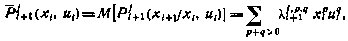
где элементы 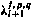выражаются через коэффициенты 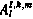и стати­стические характеристики возмущения. Полагая начальное прибли­жение 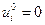, согласно (5.45) получаем в первом приближении сле­дующий закон управления:

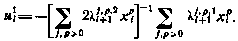
Ограничимся этим приближением. Тогда для функции будущих потерь получим

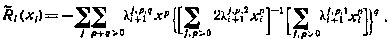
Выражения для коэффициентов 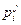в разложении

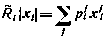
при этом принимают вид

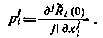
Ограничиваясь тем или иным числом членов в разложении, мож­но получить с различной степенью точности искомое решение за­дачи.

Специфика рассмотренного метода такова, что его применение целесообразно в случаях, когда управление является неограничен­ным, а ожидаемая траектория движения сравнительно близка к началу координат. Если эти условия не имеют места, более пред­почтительным может оказаться другой подход.

2. Наилучшее приближение функции потерь. Представим функ­цию потерь в виде

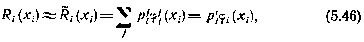
где 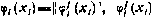- заданные функции; 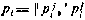— параметры, подлежащие определению. Для их определения потре­буем, чтобы 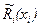как можно ближе было к действительной функ­ции 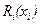в некоторой области . В качестве критерия близости рассмотрим интегральную квадратичную ошибку

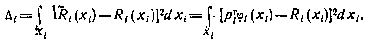
Минимизируя это выражение по 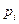, получаем

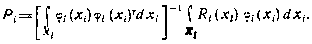
Вообще говоря, полученным соотношением можно воспользо­ваться, если функция 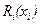известна. Но для приближенного ре­шения задачи вместо 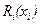можно рассмотреть функцию 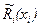, получаемую с помощью основного рекуррентного соотношения с учетом представления (5.46):

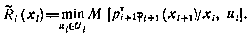
Итак, подставляя 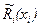в выражение для 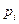, получаем следую­щее рекуррентное соотношение для определения вектора парамет­ров:

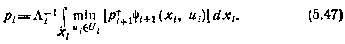
Здесь введены обозначения

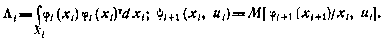
Граничные условия для вектора 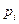получаются из соотношения

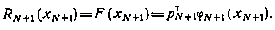
Последний метод является достаточно гибким. Он допускает использование различных разложений (5.46) для различных момен­тов времени. Так как точность метода при выбранных функциях 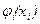зависит от областей 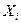, на которых производится аппрокси­мация, то их следует подбирать, как можно уже, но так, чтобы они содержали все возможные реализации векторов 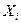. В связи с этим подбор областей 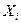целесообразно производить последовательными приближениями, чередуя процедуру определения структуры управ­ления при заданных областях 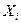с процедурой уточнения самих об­ластей 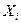путем определения статистических характеристик системы при найденном алгоритме.

Комбинированный метод оптимизации. Практически при реше­нии сложной технической задачи, связанной с оптимизацией стоха­стической системы при различных ограничениях, трудно рассчиты­вать на успех, если заранее ориентироваться лишь на один из рас­смотренных методов. Это объясняется тем, что каждый из методов,, обладая тем или иным преимуществом перед другими методами,, имеет и слабые стороны, с которыми на определенной стадии реше­ния задачи приходится сталкиваться. В связи с этим, очевидно, наиболее целесообразным является применение различных комби­нированных методов.

Рассмотрим один из таких методов на примере задачи оптими­зации процесса управления системой

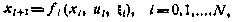
из условия обращения в минимум критерия

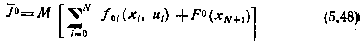
при наличии ограничений

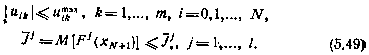
Сущность метода сводится к следующему.

1. Учет терминальных ограничений произведем с помощью мно­жителей Лагранжа, благодаря чему от исходной задачи перейдем: к вспомогательной задаче минимизации обобщенного критерия оп­тимальности:

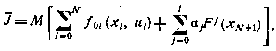
решаемой теперь уже без учета терминальных ограничений, но с последующим выбором множителей 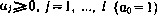так, чтобы для оптимального решения выполнялись условия

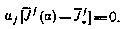
2. В искомом управлении, характеризуемом вектором и, выде­лим две составляющие — программную 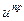и синтезируемую 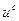. По отношению к этим составляющим применим поэтапную оптимиза­цию, согласно которой

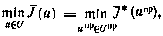
где

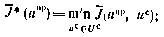
через 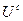, 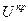обозначены множества допустимых векторов 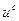, 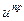соответственно. В общем случае 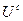зависит от .

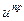На первом этапе определяется функция 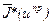путем миними­зации обобщенного критерия оптимальности 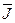по составляющей 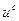. На втором этапе находится составляющая 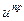путем минимиза­ции критерия .

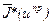Компонентами синтезируемой составляющей могут являться ли­бо компоненты вектора приращения 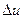относительно программной составляющей 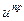[34], либо просто отдельные компоненты векто­ра и, в отношении которых желательно получить решение задачи синтеза. Для определенности здесь будем считать, что

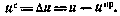
3. Для решения задачи первого этапа применим один из при­ближенных методов синтеза, изложенных выше. В частности, при совместном использовании метода динамического программирова­ния и метода статистической линеаризации получим алгоритм субоптимального управления в виде (5.39). Соответствующее значе­ние критерия оптимальности будет равно

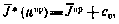
где 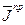определяется согласно (5.32), а с₀ — с помощью системы рекуррентных соотношений (5.41), (5.42).

4. Для решения задачи второго этапа в общем случае следует применять численные методы.

5. Решение задачи заканчивается поиском вектора множителей Лагранжа 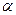. Для раскрытия зависимостей 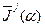представим 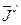в виде

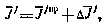
где

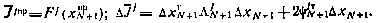
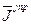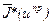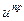Величины могут быть вычислены одновременно с минимиза­цией функции по , а 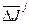одновременно с определением за­кона 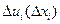. При этом возможны два подхода.

Первый основан на использовании системы (5.42) для математи­ческого ожидания и корреляционной матрицы вектора 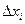при най­денном управлении. В этом случае имеем

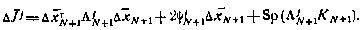
Второй подход базируется на использовании рекуррентного соот­ношения для функции

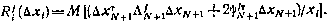
Нетрудно убедиться, что функция 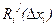имеет вид

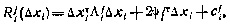
где 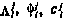удовлетворяют рекуррентным соотношениям

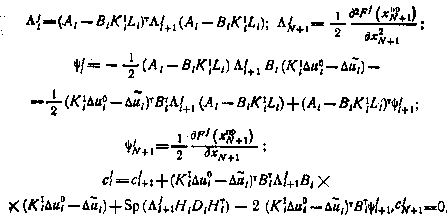
Полагая i=0 и учитывая 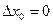, получаем

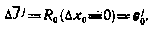
Возможны различные модификации изложенного метода. В част­ности, применение метода множителей Лагранжа может быть осу­ществлено не перед поэтапной оптимизацией, а на первом этапе ее при определении синтезируемой составляющей управления.

Применение метода поэтапной оптимизации проиллюстрируем на примере задачи оптимизации процесса управления системой

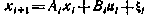
из условия обращения в минимум критерия

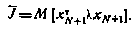
Пусть начальное состояние х₀ считается известным. Для просто­ты ограничимся случаем скалярного управления. Обозначим через 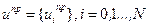последовательность программных значе­ний управляющего воздействия, через 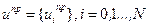— соответствующую траекторию 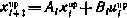. Значение кри­терия при этом будет равно

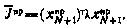
Учитывая, что в данном случае 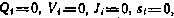, со­гласно (5.36) — (5.37) получим следующие расчетные формулы:

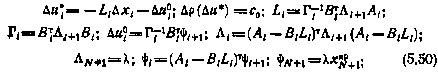
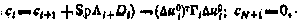
из которых видно, что конкретная программа управления влияет лишь на компенсационную составляющую 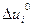через вектор 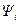и соответственно на величину критерия 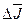. Коэффициенты обратной связи 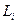оказываются инвариантными относительно программы уп­равления.

Для определения оптимальной программы, управления зададим

начальное приближение 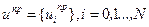, обеспечивающее

минимум критерию 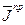. Нетрудно установить, что для всех 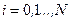имеет место соотношение .

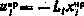Вычислим составляющие градиента 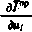. Так как 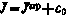и

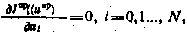
получим

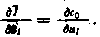
Оказывается, что все производные 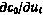при этом также обра­щаются в нуль. Действительно, из (5.50) с учетом 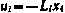следу­ет, что

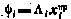
и

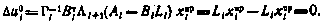
Поэтому для любого i

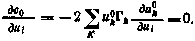
Таким образом, оптимальная программа управления в данной задаче минимизирует составляющую и может рассматриваться как результат применения оптимального закона управления к осредненному процессу.