Фильтр Калмана алгоритм оценивания линейный байесовский

Рассмотрим постановку байесовской задачи оценивания для линейных моделей динамической системы и измерений. Пусть дискретная модель динамической системы имеет вид

где —я-мерный вектор состояния системы; и—m-мерный вектор управления; -мерный вектор случайных возмущений; — матрицы размерностей п×п и п×т соответственно с элементами, зависящими в общем случае от номера i.

В общем случае в число компонент вектора состояния системы (3.13) входят, помимо компонент, характеризующих ее положение и скорость (например, координаты и скорость летательного аппа­рата), составляющие возмущений. Эти возмущения в общем случае также подлежат оцениванию, например, в случае движения ЛА в атмосфере могут оцениваться скорости порывов ветра, отклоне­ния плотности атмосферы от стандартной, систематические ошибки измерений и т. д. Вектор состояния , включающий, помимо со­ставляющих положения и скорости, различные возмущения, при­нято называть расширенным или обобщенным.

Закон управления, т. е. способ формирования вектора управле­ния 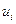на основе оценок, считается заданным. Таким образом, рассматривается управляемое движение системы с обратной связью. В общем случае вектор управления может реализоваться со слу­чайной ошибкой.

Считаем, что векторы начальных условий х₀ и возмущений независимы и подчиняются нормальному закону распределения:

где — априорная корреляционная матрица вектора ап­риорное математическое ожидание х₀.

где — корреляционная матрица вектора .

В силу линейности модели (3.13) и гауссовости векторов априорная плотность вероятностей p( ) оцениваемого вектора также является гауссовой:

где — априорная корреляционная матрица вектора - ап­риорное математическое ожидание вектора .

Измерения осуществляются дискретно в моменты , которые считаются известными. Уравнение измерений имеет вид

где -мерный вектор измерений; 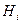— матрица l×п, элементы которой зависят от номера i; -мерный вектор ошибок измере­ний— вектор независимых центрированных случайных величин, распределенных по нормальному закону:

Требуется найти рекуррентный байесовский алгоритм оценива­ния вектора состояния системы (3.13) по измерениям , где 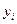соответствует (3.17).

Введем квадратичную функцию потерь вида (3.1)

где 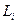— симметричная положительно определенная матрица, не­особенная при всех i, и байесовский риск

В (3.19) и (3.20) подразумевается, что —искомый алго­ритм оценивания.

Условие минимума no имеет вид (правила вектор­ного дифференцирования см. в приложении 4)

откуда с учетом неособенности матрицы получаем байесовскую оценку для :

Таким образом, при квадратичной функции потерь байесовская оценка состояния системы (3.13) представляет собой математиче­ское ожидание вектора ,соответствующее апостериорной плот­ности вероятностей . Это математическое ожидание также будем называть апостериорным. Оно определяется при фиксирован­ном векторе , т. е. , и не зависит от матрицы , т. е, оценка инвариантна по отношению к .

Этот вывод и будет положен в основу получения соответствую­щего байесовского алгоритма оценивания.

Заметим, что в соответствии со свойствами матриц и квадра­тичных форм (3.20) можно переписать в виде

где

- кор­реляционная матрица, соответствующая апостериорной плотности вероятностей . В дальнейшем будем называть апостери­орной корреляционной матрицей вектора . Символ Sp означает •след матрицы.

Рассмотрим момент времени . Нам известен вектор , а также вектор управления 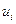, переводящий систему из состоя­ния в состояние 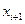. Будем считать вначале, что вектор 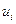реа­лизуется без ошибок.

Запишем апостериорную плотность вероятностей вектора 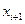для чего воспользуемся формулой Байеса (3.11). До­казано [4], что последовательность измерений обладает мар­ковскими свойствами при заданных значениях марковской после­довательности , i = 0, 1, 2, .... Формулу Байеса запишем в следующем виде:

В отличие от формулы Байеса в виде (1.9) или, что то же самое, (3.11), в правой части (3.24) фигурирует дополнительное условие фиксации ,т. е. последовательности векторов измерений . Необходимость в этом условии состоит в следующем. Необходи­мо получить рекуррентный алгоритм, в котором векторы измерений обрабатывались бы поочередно. Это значит, что при поступлении вектора вычисляем оценку, соответствующую всей совокупно­сти имеющихся к данному моменту измерений , как функцию оценки, полученную по результатам измерений и измерения . Эта оценка будет тождественная оценке, полученной в результате обработки всей совокупности измерений , только в том случае, если последовательность —марковская.

Заметим, что как следует из (3.22), математическое ожидание вектора 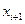соответствующее плотности вероятностей , входящей в правую часть (3.24), есть байесовская оценка 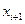по измерениям при квадратичной функции потерь. Эту оценку на­зовем прогнозированной и обозначим , а корреляционную мат­рицу, соответствующую плотности вероятностей .

В силу линейности соотношения (3.13) с учетом независимости и центрированности и имеем

где

— корреляционная матрица, соответствующая плотности вероятно­стей . Назовем ее апостериорной.

Плотность вероятностей с учетом обозначения (3.27) запи­шется в виде

В силу линейности моделей (3.13), (3.17) и гауссовости векто­ров 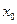, и плотность вероятностей также гауссовская:

Вследствие тех же причин плотность вероятностей , входящая в правую часть (3.24),— гауссовская с характеристи­ками

Следовательно,

Определим теперь характеристики плотности вероятностей . Как и другие плотности вероятностей, входящие в правую часть (3.24), она гауссовская. Согласно (3.15), (3.17), (3.25) можем записать

Из (3.33) и (3.34) следует

Подставив (3.29), (3.32) и (3.35) в правую часть (3.24), получим

Выражение (3.37) можно привести к квадратичной форме вида

где через и обозначены характеристики плотности веро­ятностей . Преобразование (3.37) к виду (3.38) осуще­ствляется с помощью матричного тождества

в предположении, что матрицы Л и С, т. е. — невырож­денные. Характеристики плотности вероятностей с уче­том (3.37) и (3.38) соответственно равны

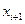Запишем окончательно выражения, позволяющие вычислить байесовскую оценку вектора по измерениям при из­вестной байесовской оценке вектора по измерениям . Эти соотношения определяют дискретный фильтр Калмана:

Из выражения (3.43), определяющего апостериорную корреля­ционную матрицу следует, что эта матрица, характеризую­щая точность получаемых оценок, может быть определена незави­симо от измерений , т. е. рассчитана заранее.

«Начальными условиями» для соотношений (3.42) — (3.45) яв­ляются

Равенства (3.46) означают, что в момент t = 0, соответствующий началу процесса оценивания, в качестве прогнозированной оценки вектора 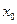следует принять его априорное математическое ожида­ние , а в качестве априорной корреляционной матрицы—соот­ветствующую характеристику априорной плотности вероятностей р( 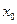). Пусть случайное возмущение содержит, помимо аддитив­ной, мультипликативную составляющую, зависящую от величины управляющего воздействия, т. е.

где 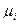- — независимая центрированная случайная величина, подчи­няющаяся гауссовскому распределению с дисперсией ( , a — вектор независимых центрированных величин, подчиняющихся га­уссовскому распределению с корреляционной матрицей . В этом

случае корреляционная матрица вектора 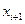при фиксирован­ных зависит от конкретного значения :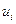

Итак, если в модели движения динамической системы предполага­ется наличие обратной связи , то при мультипликативной ошибке реализации управляющего воздействия корреляционная матрица и, следовательно, апостериорная корреляционная мат­рица не могут быть рассчитаны независимо от процесса из­мерений.

В ряде случаев весьма полезными оказываются соотношения непрерывного фильтра Калмана, которые могут быть получены из соотношений (3.42) — (3.45) с помощью предельного перехода.

Непрерывный фильтр Калмана предполагает наличие соответст­вующей модели движения оцениваемой динамической системы

и непрерывного процесса измерений

Размерности и смысл векторов и матриц в моделях (3.49) и (3.50) те же, что и в моделях (3.13) и (3.17) соответственно.

Векторы случайных начальных условий 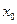, ошибок измерений 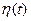и возмущений 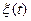статистически независимы и подчиняются нормальным законам распределения с характеристиками

Таким образом, ошибки измерения и возмущения 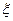представ­ляют собой белые шумы.

Обратимся к приведенным выше дискретным аналогам (3.13), (3.17) моделей (3.49), (3.50). Предположим, что интервал времени между измерениями настолько мал, что в дискретных моделях можно принять

где I — единичная матрица.

Подставляя (3.52) в соотношения (3.42) — (3.45), определяю­щие дискретный фильтр Калмана, получаем

где символом о обозначены члены, зависящие от ,

Подставляя (3.54) в (3.55) с учетом малости членов о и пола­гая, что , получаем дифференциальные уравнения для апостериорного математического ожидания и апостериорной корреляционной матрицы вектора х:

Соотношения (3.56) и (3.57) определяют непрерывный фильтр Калмана. Как и в дискретном случае, при отсутствии мультиплика­тивных возмущений , матрица Р* может быть определена незави­симо от процесса измерения. Начальными условиями для уравне­ний (3.56), (3.57) служат равенства

Фильтр Калмана находит широкое применение в различных об­ластях техники. В частности, он используется для оценивания па­раметров движения как при автономном управлении движением летательных аппаратов, так и при командном управлении.