Каноническое разложение случайных процессов

В некоторых случаях для описания случайного процесса применяют его представление через сумму случайных процессов более простого вида. Один из способов такого представления назы­вается каноническим разложением [32]. При каноническом разло­жении случайный процесс представляют в виде

где m_x(t)—математическое ожидание процесса; — координатные функции, являющиеся заданными неслучайными функциями времени; V_i — коэффициенты, являющиеся некоррели­рованными случайными величинами с нулевыми математическими ожиданиями и дисперсиями .

В качестве координатных функций в канонических разложениях используют семейства функций, обладающих свойством ортонормированности:

Корреляционная функция случайного процесса (1.53) выража­ется через его каноническое разложение так:

Суммирование по переменной R исчезает, поскольку вследствие некоррелированности случайных величин и .

Полагая t₁ = t₂=t, из (1.54) получаем выражение для дисперсии

При практических расчетах ограничиваются конечным числом чле­нов канонического разложения. Методика построения канонических разложений случайных процессов изложена в книге [32].

Спектральная плотность

Наряду с корреляционной функцией для статистического описания стационарных случайных процессов используют спектраль­ную плотность 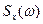. Так называют функцию частоты 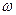, являю­щуюся обратным интегральным преобразованием Фурье от корре­ляционной функции 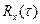случайного процесса x(t):

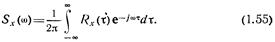
В свою очередь, корреляционная функция процесса x(t) выра­жается через его спектральную плотность как прямое интеграль­ное преобразование Фурье:

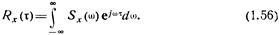
Полагая в (1.56) 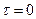, получаем выражение для дисперсии D_x стационарного случайного процесса x(t) через его спектральную плотность:

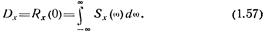
Если в (1.55) и (1.56) перейти к тригонометрической форме представления 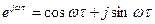и 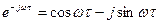, то получим

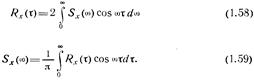
При описании стационарных случайных процессов вместо 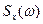может задаваться спектральная плотность, определяемая для поло­жительных частот:

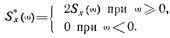
В этом случае корреляционная функция процесса должна вычис­ляться по известной спектральной плотности 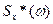с помощью со­отношения

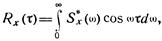
а дисперсия D_x определяется с помощью формулы

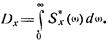
Последнее выражение позволяет дать физическую интерпрета­цию спектральной плотности 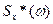: она характеризует плотность распределения дисперсии стационарного случайного процесса по частотам непрерывного спектра гармонического разложения этого процесса.

Рассмотрим два примера определения спектральных плотностей стационарных случайных процессов по их корреляционным функ­циям.

Белый шум.Для белого шума 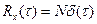, поэтому из (1.59) находим, учитывая свойство 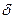-функции,

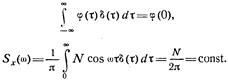
Как видим, спектральная плотность белого шума остается по­стоянной на бесконечном интервале частот. Это указывает на физи­ческую нереализуемость такого шума, поскольку для его реализа­ции потребовалась бы бесконечно большая энергия источника тако­го шума. Равномерное распределение дисперсии на бесконечном интервале частот может также использоваться в качестве иного определения белого шума. Спектр солнечного света в оптическом диапазоне близок к равномерному. Учитывая эту аналогию, случай­ный процесс с равномерной спектральной плотностью называют бе­лым шумом. Все другие случайные процессы, у которых функция .S'_x(co) меняется по частоте, можно называть «окрашенными» шума­ми. На практике в качестве белого рассматривают любой окрашен­ный шум, спектральная плотность которого остается постоянной в пределах полосы пропускания системы, на которую этот шум дей­ствует.

Экспоненциально коррелированный процесс.Случайный про­цесс с корреляционной функцией вида

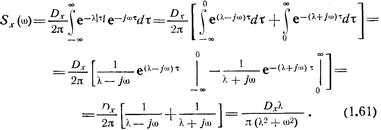
называют экспоненциально корреляционным. Спектральную плот-кость такого процесса можно найти с помощью формулы (1.55)

СЛУЧАЙНЫЕ ПОЛЯ

При исследовании управляемого движения летательных аппаратов некоторые факторы, как, например, плотность, темпера­тура, турбулентность в реальной (не стандартной) атмосфере, изме­няются случайно в зависимости от координат рассматриваемой точ­ки пространства и времени t.

Случайные факторы, аргументами которых являются векторы, называют случайными полями.

Если в состав компонент вектора аргументов поля входят только координаты пространства, то такое случайное поле называют про­странственным. Если же в состав аргументов поля входит также и время, то случайное поле называют пространственно-временным.

Случайные поля бывают скалярными и векторными. Плотность воздуха в атмосфере р(х, у, z, t) и его температура Т(х, у, z, t) — скалярные пространственно-временные случайные поля. Турбулент­ность атмосферы w(x, у, z, t) есть векторное пространственно-вре­менное случайное поле, поскольку скорость порывов ветра в турбу­лентной атмосфере да— это вектор, характеризуемый тремя состав­ляющими w_x, w_v, w_z.

Скалярные случайные поля

Обозначим вектором х= {х, у, z} вектор аргументов про­странственного скалярного случайного поля и(х). Вектор х опреде­лен в области D возможного изменения координат х, у, z. Точку 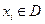назовем точкой наблюдения поля. В каждой точке скаляр­ного поля наблюдается скалярная случайная величина .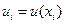

Скалярное случайное поле и(х) считается описанным полностью, если для произвольного числа точек наблюдения 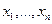известен способ построения «-мерного совместного безусловного распреде­ления вероятностей 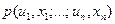системы случайных величин .

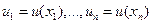В частности, если при любых 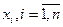, и любом п справедливо соотношение

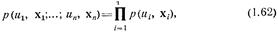
то поле и(х) называется абсолютно случайным, и для его описания достаточно задать зависимость одномерной плотности р_u(х) от ко­ординат х точки наблюдения этого поля.

Как и при описании случайных величин и процессов, для описа­ния случайных полей часто пользуются их моментными характерис­тиками.

n-точечным начальным моментом порядка t_i + ... + i_n скалярно­го поля и(х) называется математическое ожидание произведения соответствующих степеней возможных значений поля в n точках наблюдения:

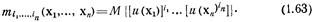
Одноточечный начальный момент первого порядка

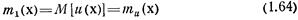
называется математическим ожиданием скалярного случайного поля. Оно характеризует среднее значение случайной величины и в каждой точке х области D.

Разность 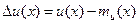есть центрированное случайное поле. Среднюю величину произведения степеней 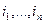возмож­ных значений центрированного поля 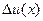в n точках наблюдения называют «-точечным центральным моментом порядка :

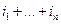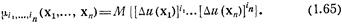
Одноточечный центральный момент второго порядка

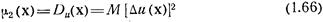
есть дисперсия скалярного поля u(х), а двухточечный центральный момент второго порядка

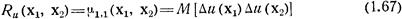
— его корреляционная функция. Дисперсия случайного поля харак­теризует рассеивание случайных значений поля в точке наблюде­ния, а корреляционная функция — корреляцию значений поля в двух его точках наблюдения х₁ и х₂.

Скалярное случайное поле может обладать свойствами однород­ности и изотропности. Поле и(х) называется однородным (строгая однородность), если его n -точечное совместное распределение не изменяется при переносе точек наблюдения этого поля 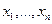на один и тот же вектор х₀, т. е.

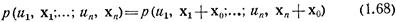
при любом х₀ и любом числе точек наблюдения п.

Скалярное случайное поле u(х) называется однородным в широ­ком смысле, если его математическое ожидание т_u(х) является постоянным во всех точках области D, а корреляционная функция 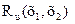не изменяется при переносе пары точек наблюдения х₁ и х₂ на один и тот же вектор х₀, т. е.

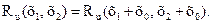(1.69)

Иными словами, аргументом корреляционной функции однородно­го скалярного поля являются не координаты х₁ и х₂ точек наблю­дения этого поля, а вектор 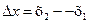соединяющий эти точки в области D. Свойство однородности скалярного случайного поля эквивалентно свойству стационарности случайного процесса.

Однородное скалярное поле u(х) называется изотропным, если корреляция между значениями этого поля в точках х₁ и х₂ не зави­сит от ориентации вектора 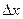, а зависит только от его длины 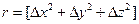. Таким образом, в рамках корреляционной теории изотропное скалярное случайное поле u(х) описывается двумя ха­рактеристиками: математическим ожиданием m_u(x)=const и кор­реляционной функцией R_u(r).

Векторные случайные поля

Рассмотрим векторное пространственное случайное по­ле и(х), у которого аргумент х - вектор с координатами х, у, z, принадлежащий области наблюдения поля D, а и — вектор с проек­циями и_х, и_у, u_z.

Проекции и_х(х), и_у(х), u_z(x) можно рассматривать как совокуп­ность трех случайных полей. Статистическое описание этой совокуп­ности эквивалентно статистическому описанию векторного поля и(х). В рамках корреляционной теории для описания совокупности скалярных случайных полей и_х(х), и_у(х) и u_z(x) требуется задать вектор их математических ожиданий т_и(х) и матричную корреля­ционную функцию 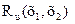. Вектор математических ожиданий со­стоит из трех компонент 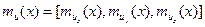, каждая из которых есть математическое ожидание соответствующей со­ставляющей вектора и в точке наблюдения х.

Матричная корреляционная функция 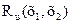характеризует статистическую взаимосвязь между различными компонентами век­тора и в двух различных точках наблюдения поля х₁ и х₂ в облас­ти D:

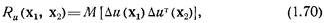
где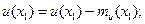

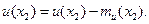
Если поле ы(х), у которого аргумент х состоит из трех компо­нент х, у, z, содержит три компоненты и_х, и_у, и_z, то матричная кор­реляционная функция 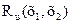имеет размерность 3×3. Элементы 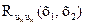, 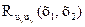и 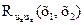— автокорреляционные функции составляющих и_х, и_у и и_z векторного поля; остальные эле­менты— взаимные корреляционные функции между различными составляющими этого поля. Например, корреляция между компо-

нентами и_х и и_у в точках наблюдения х₁ и х₂ характеризуется вза­имной корреляционной функцией

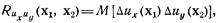
где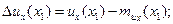

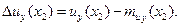
При х₁-х₂=х, т. е. при совпадении двух точек наблюдения, матричная корреляционная функция 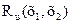векторного случай­ного поля u(х) обращается в его корреляционную матрицу K_u(x), диагональными элементами которой являются дисперсии составля­ющих и_х, и_у, u_z вектора и в точке х, а внедиагональными — взаим­ные корреляционные моменты этих составляющих.

Как и скалярное, векторное случайное поле может быть одно­родным и изотропным. Статистические характеристики однородно­го векторного случайного поля u(х) инвариантны относительно па­раллельного переноса точек наблюдения поля в области D на оди­наковый вектор х₀ произвольной длины. Для такого поля математи­ческое ожидание есть постоянный вектор 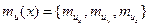, a матричная корреляционная функция 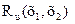зависит только от вектора 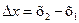соединяющего точки наблюдения х₁ и х₂, и не зависит от положения точки х₁ начала вектора 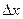в области D.

Для рассмотрения свойства изотропности однородного вектор­ного пространственного случайного поля введем две системы коор­динат: абсолютную (неподвижную) и подвижную. Однородное векторное случайное поле называется изотропным, если его момент-ные характеристики инвариантны не только по отношению к парал­лельным переносам точек наблюдения поля, но также относительно их произвольных вращений и зеркальных отображений совместно с вращениями и зеркальными отображениями осей подвижной систе­мы координат относительно абсолютной системы координат.

Из определения свойства изотропности однородного векторного случайного поля следует, что такое поле должно иметь нулевой век­тор математических ожиданий , а матричная корреляцион­ная функция R_u(r), где , должна быть диаго­нальной. Все взаимные корреляционные функции, входящие в R_u(r), равны нулю. Одна из трех ненулевых автокорреляционных функций изотропного векторного поля характеризует корреляцию между проекциями и_r(х₁) и и_r(х₂) вектора u(х) на вектор r, соединяющий две рассматриваемые точки наблюдения поля. Эту автокорреляци­онную функцию изотропного поля R_r(r) =M[u_r(x), u_r(x + r)] назы­вают продольной. Две другие автокорреляционные функции и изотропного поля одинаковы: . Каж­дая из них характеризует корреляцию между параллельными проек­циями и_n(х) и и_n(х+r), перпендикулярными вектору г, в точках х и x+r:

Таким образом, для полного описания изотропного векторного случайного поля в трехмерном пространстве в рамках корреляцион­ной теории требуется задать две его корреляционные функции: u .

От матричной корреляционной функции R_u(r) изотропного век­торного случайного поля и(х) можно перейти к матричной спек­тральной плотности этого поля. Как и R_u(r), матричная спектральная плотность есть квадратная диагональная мат­рица 3×3 с элементами

Аргументом 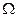в спектральных плотностях и явля­ется волновое число, размерность которого обратна размерности r.