Определение и классификация случайных процессов

Если некоторая переменная х зависит от скалярного ар­гумента t и при каждом фиксированном значении последнего явля­ется случайной величиной, то переменную х(t) называют случайной функцией.

Если аргументом t у переменной x(t) является время, то такую случайную функцию называют случайным процессом. Например, угол тангажа 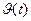летательного аппарата, движущегося в турбу­лентной атмосфере, является случайным процессом.

Если х—вектор, то зависимость x(t) —векторный случайный процесс. Например, движение центра масс летательного аппарата по траектории характеризуется шестимерным вектором x(t) = {х, у, z, V_x, V_y, V_z}. Если движение аппарата происходит при действии случайных факторов, то x(t) —векторный случайный процесс.

В отдельных опытах наблюдаются реализации xⁱ(t), i-1, 2, ... случайного процесса x(t); i — номер реализации.

Статистическое описание случайного процесса x(t) осуществля­ют, рассматривая множество случайных величин x₁ = x(t₁), ..., x_i= x(t_i), соответствующих различным значениям времени t, взятым на рассматриваемом интервале его изменения 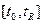. Считается, что произвольный случайный процесс x(t) описан полностью, если указан способ построения последовательности плотностей вероят­ности р(х, t); p(x₁, t; x₂, t₂); ...; р(x₁, t₁; ...; х_п, t_n) при 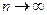, где .

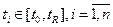Одномерная плотность р(х, t) позволяет определить вероятность попадания случайной величины x(t) в интервал :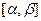

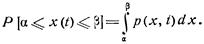
С помощью двумерной совместной плотности 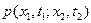оп­ределяют, с какой вероятностью две случайные величины х₁ и х₂ по­падут в интервалы 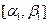и 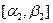, соответствующие моментам t₁ и t₂:

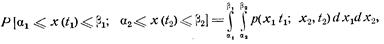
и так для любого п.

Для описания случайных процессов могут также использоваться условные плотности распределения вероятностей. Условная плот­ность вероятности 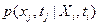характеризует распределение веро­ятностей случайной величины 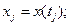, реализации которой в мо­мент 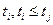прошли через точку 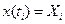. Аналогично условная плотность 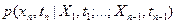есть плотность распределе­ния вероятностей случайной величины x_n = x(t_n), реализации кото­рой в предшествующие моменты 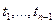принимали фиксирован­ные значения 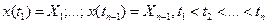. С учетом формулы (1.7) справедливы следующие соотношения между сов­местными безусловными и условными распределениями:

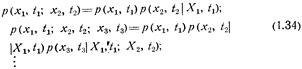
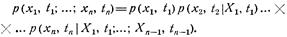
Имеют место следующие предельные свойства безусловных и условных распределений:

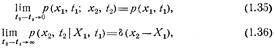
где 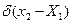—дельта-функция в точке Х₁.

В другом предельном случае

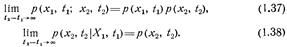
Классификацию случайных процессов осуществляют в зависи­мости от тех свойств, которыми обладают их совместные безуслов­ные и условные распределения.

Абсолютно случайный процесс. Процесс x(t) называют абсо­лютно случайным, если случайные величины 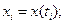и 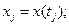независимы при сколь угодно малом 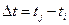. Учитывая (1.10), для такого процесса получим, что совместное n-мерное распределе­ние при любом п. определяется соотношением

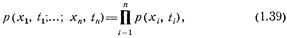
т. е. абсолютно случайный процесс полностью описывается его одно­мерным распределением р(х, I), известным для каждого t.

Марковский процесс. Зададим на интервале 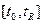возможного изменения аргумента t случайного процесса x(t) временной ряд 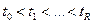. Случайный процесс x(t) называют марковским, если для него справедливо соотношение для любых .

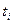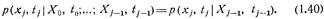
Для марковского процесса условная плотность вероятности слу­чайной величины 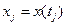зависит только от того, каким было зна­чение случайной величины 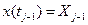и никак не зависит от того, каким были реализации 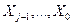данного процесса в предыдущие моменты 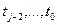. Плотность 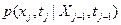называют также переходной плотностью вероятности марковского процесса x(t). Для марковского процесса x(t), учитывая (1.34) и (1.40), имеем

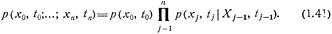
Как видим, для исчерпывающего описания марковского случай­ного процесса достаточно задать его начальную одномерную плот­ность вероятности 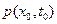и переходные плотности .

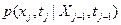Марковский процесс с независимыми приращениями. Случайный процесс x(t) называют процессом с независимыми приращениями, если для любых значений 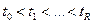, выбранных на интервале 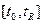, приращения 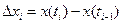, 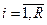— независимые случайные величины. Процесс с независимыми приращениями - также марковский, так как значение случайной величины x(t_i) в конце каждого интервала 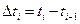определяется предыдущим значением 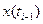и приращением на этом интервале, не зависящим от приращений на предшествующих интервалах.

Гауссовский случайный процесс.Случайный процесс x(t), у ко­торого совместная n-мерная плотность вероятности 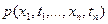при любом п и любых 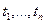является гауссовской, называется гауссовским случайным процессом.