Скалярные и векторные случайные величины

Случайные величины бывают скалярными и векторными. Исчерпывающей характеристикой скалярной случайной величины х является ее функция распределения вероятностей 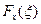, определяю­щая вероятность того, что случайная величина х примет значение, не превосходящее заданную величину 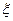, т. е.

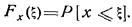
Производная от функции распределения называется плотностью распределения или плотностью вероятности случайной величины х:

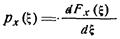
В дальнейшем для упрощения обозначений функцию распределения вероятностей обозначим через F(x), а плотность вероятности 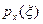—через р(х).

Плотность р(х) скалярной случайной величины х обладает сле­дующими свойствами:

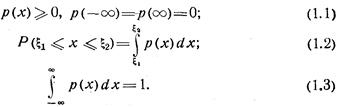
Несколько скалярных случайных величин х₁, ..., х_n, рассматри­ваемых совместно, образуют векторную случайную величину х. Ее статистические свойства описываются полностью n-мерной плотно­стью вероятности р(х) =р(х₁, ..., х_n).

Как и для скалярной случайной величины, плотность вероятности р(х) случайного вектора всегда неотрицательна, а соотношение (1.1) — (1.3) трансформируются в следующие:

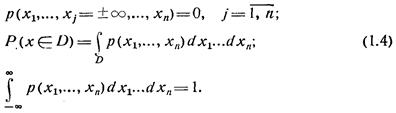
В формуле (1.4) через 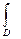обозначен n-мерный интеграл по облас­ти D в пространстве переменных х₁, ..., х_n.

Зная плотность вероятности р(х) вектора х, можно определить плотности вероятности отдельных составляющих этого вектора. Пусть, например, требуется найти р(y), где 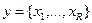, 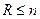. Обозначим остальные п—R составляющих вектора х через .

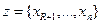Тогда

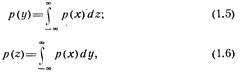
где dy = dx₁...dx_R; dz=dx_R+1...dx_n.

Плотность вероятности р(х) устанавливает вероятностную зави­симость между составляющими случайного вектора х. Эта зависи­мость может быть также охарактеризована с помощью условной плотности вероятности. Обозначим через 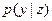условную плот­ность вероятности случайного вектора у размерности R при усло­вии, что случайный вектор z принял определенное значение z = Z, и через 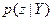- условную плотность вероятности вектора z раз­мерности п—R при условии y=Y. 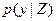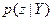Если х={у, z}, то совместная плотность р(х) связана с условными плотностями вероятности и соотношениями

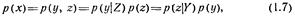
где р(у) и p(z)—соответственно плотности вероятности векторов y и z.

Из формулы (1.7) с учетом (1.5) и (1.6) следуют выражения для условных плотностей вероятности

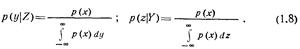
Заменяя в первом выражении в (1.8) плотность р(х) через 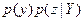получаем

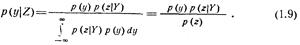
Соотношение (1.9) называется формулой Байеса. Оно выража­ет связь между условными плотностями вероятност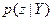и и 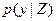. Аналогично записывается и обратная формула:

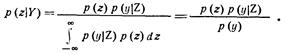
Векторные случайные величины y и z называют независимыми, если р(у, z)=p(y)p(z). Из формулы (1.7) следует, что для неза­висимых случайных векторов у и z справедливо выражение 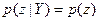при любом y=Y и 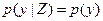— при любом z=Z.

Если вектор х состоит из п независимых составляющих х₁, ..., х_n, то плотность вероятности р(х) такого вектора равна произведению плотностей его составляющих:

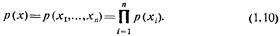
Моменты случайных величин

Моменты служат для описания основных свойств плотно­сти вероятности случайной величины. Они содержат меньше инфор­мации о случайной величине по сравнению с плотностью вероятно­сти, но часто более удобны при решении технических задач. В каче­стве моментов скалярной случайной величины чаще всего применяются математическое ожидание и дисперсия (или среднеквадратическое отклонение).

Математическим ожиданием некоторой функции y = f(x) случай­ной величины х называется интеграл

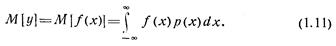
При f(x) = x^R величина M[x^R]=m_x^R называется начальным моментом R-го порядка случайной величины х. Начальный омент пер­вого порядка т_х называется математическим ожиданием случайной величины х:

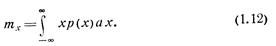
По реализациям 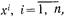математическое ожидание т_х может быть оценено как статистическое среднее

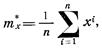
причем .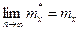

Разность 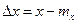менаду случайной величиной х и ее мате­матическим ожиданием т_х называется центрированной случайной величиной. Центральный момент R-го порядка скалярной случайной величины х определяется как математическое ожидание R-й степени соответствующей центрированной случайной величины:

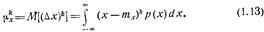
Центральный момент второго порядка 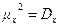называется дис­персией случайной величины х:

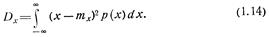
По реализациям 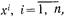оценку 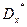можно рассчитать по формуле

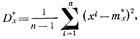
причем .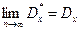

Дисперсия характеризует рассеивание значений случайной вели­чины х в окрестности ее математического ожидания т_х. Наряду с дисперсией D_x в качестве меры рассеивания рассматривают и среднеквадратическое отклонение .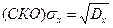

Центральные моменты высших порядков определяют аналогич­но. Например, центральный момент третьего порядка

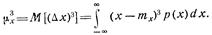
Он характеризует асимметрию кривой плотности вероятности р(х). Если р(x) —симметричная функция с осью симметрии, проходящей через т_х, то 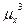, а также все другие нечетные центральные момен­ты случайной величины х равны нулю.

В качестве характеристик вероятностной зависимости двух ска­лярных случайных величин х и у рассматривают их корреляцион­ный момент

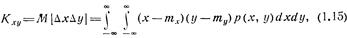
или коэффициент корреляции

вычисляемый пр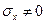и и .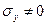

По реализациям хⁱ, уⁱ, i= 1, п, случайных величин x и y их корре­ляционный момент можно оценить с помощью соотношения

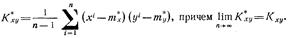
Если случайные величины х и у связаны между собой линейной зависимостью у = ах + b, где а и b — произвольные неслучайные числа, то 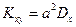, а r_xy=1 при а>1 и r_xy = -1 при а<0.

Случайные величины х и у называют некоррелированными, если 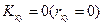. Используя формулы (1.15), (1.10), нетрудно пока­зать, что из независимости случайных величин следует их некорре­лированность. Обратное утверждение в общем случае неверно. Ина­че говоря, условие независимости случайных величин более сильное, чем условие некоррелированности.

Для векторной случайной величины х простейшими моментными характеристиками, наиболее часто рассматриваемыми при прак­тических расчетах, являются вектор математических ожиданий т_х и корреляционная матрица К_х- Составляющими вектора т_х являются математические ожидания компонент вектора х, т. е. .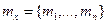

Корреляционной матрицей К_х случайного вектора х называется симметричная матрица, составленная из корреляционных моментов 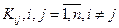, и дисперсий 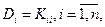составляющих век­тора х:

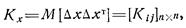
причем .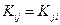

Если все составляющие случайного вектора х взаимно некорре­лированные, то этот вектор называют некоррелированным. Корре­ляционная матрица К_х некоррелированного вектора — диагональ­ная, все ее внедиагональные элементы равны нулю.

Нормальное распределение

Конкретный вид распределения случайной величины х зависит от физической природы явления. Особое место среди всевозможных распределений занимает распределение Гаусса или нормальное распределение, поскольку именно такими или близки­ми к нормальному являются распределения многих случайных ве­личин, рассматриваемых при анализе движения автоматических летательных аппаратов.

Нормальная плотность вероятности р_г(x) скалярной случайной величины х описывается выражением

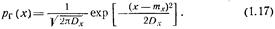
Она полностью характеризуется двумя параметрами: т_х и D_x. Пользуясь соотношениями (1.12) и (1.14), можно убедиться в том, что параметр т_х нормальной плотности вероятности есть математи­ческое ожидание, a D_x — дисперсия этой случайной величины.

В соответствии с формулой (1.2) вероятность попадания гауссовской случайной величины х в интервал 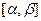равна

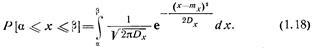
После замены переменной х на 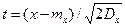вычисление интеграла в формуле (1.18) сводится к вычислению соотношения

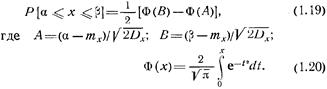
Значения функции Лапласа Ф(х), определяемой соотношением (1.20), приведены в приложении 1. При проведении расчетов на ЦВМ их можно рассчитать с помощью стандартной подпрограммы.

При преобразованиях выражений, содержащих функцию Лапла­са Ф(х), можно пользоваться следующими свойствами этой функ­ции:

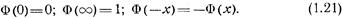
Нормальное распределение вероятностей n-мерного случайного век­тора х описывается формулой

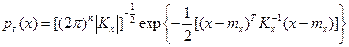
где т_х— вектор математических ожиданий; К_х — корреляционная матрица; 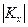- определитель корреляционной матрицы.

В евклидовом n-мерном пространстве, координатами которого являются составляющие вектора х, плотность вероятности р_г(х) постоянна на концентрических гиперэллипсоидах:

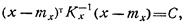
называемых гиперэллипсоидами рассеивания, где С — любое поло­жительное число. Центром гиперэллипсоидов рассеивания является точка с координатами т_х, направление главных осей совпадает с собственными векторами 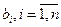корреляционной матрицы К_х, а длина каждой из главных полуосей равна 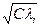, где 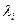— собствен­ное значение корреляционной матрицы К_х, соответствующее собст­венному вектору b_i.

В двумерном случае нормальное распределение (1.22) принима­ет вид

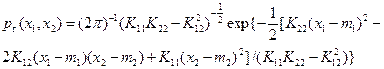(1.23)

Плотность вероятности (1.23) постоянна на эллипсах, называе­мых эллипсами рассеивания. Угол между главной осью эллипса рас­сеивания и осью Ox₁ определяется с помощью выражения [8]

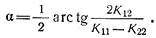
Если составляющие х₁ и х₂ вектора х некоррелированы, то на­правления главных осей эллипса рассеивания совпадают с направ­лениями осей системы координат Ох₁х₂.

На практике принято строить эллипсы рассеивания, главные по­луоси которых равны 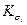где 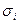— С КО соответствующей компо­ненты; К — целое число.

1.1.4. Линейные и нелинейные преобразования случайных величин

При решении задач статистического анализа и оптимиза­ции управления движением летательных аппаратов часто требуется определять моменты и распределения линейных и нелинейных функ­ций случайных величин. Например, при переходе от одной системы координат к другой требуется уметь вычислить вектор математиче­ских ожиданий и корреляционную матрицу фазового вектора, опи­сывающего состояние летательного аппарата относительно новой системы координат, если статистические характеристики фазового вектора относительно исходной системы координат известны.

Вначале рассмотрим случай линейного преобразования случай­ной величины. Пусть х и у — случайные векторы, связанные между собой линейным соотношением

где х — вектор размерности п; у — вектор размерности l; А — мат­рица размерности l×п; b — неслучайный вектор размерности l.

Используя соотношение (1.11) и учитывая (1.12), находим соот­ношение между т_х и т_у:

Вычитая (1.25) из (1.24), получаем соотношение 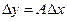между центрированными случайными величинами, из которого непосредст­венно вытекает соотношение между корреляционными матрицами К_x и К_у:

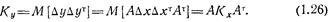
В частном случае при 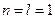, т. е. когда х и у— скалярные слу­чайные величины, имеем m_y=am_x+b; D_y=a²D_x. При п=2 и l=1, т. е. если y=a₁x₁ + a₂x₂ + b, получаем m_y = a₁m₁+ a₂m₂ + b и 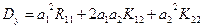, где K₁₁, K₁₂, K₂₂, - элементы корреляци­онной матрицы К_x-

В случае нелинейной зависимости y=f(x), где x — скаляр,

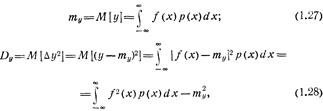
т. е. для нахождения m_y и D_y недостаточно знать т_х и D_x, а долж­на быть известна плотность вероятности р(х) аргумента х.

Пример.Рассмотрим преобразование гауссовской случайной величины х не­линейным звеном типа «реле» с уровнем насыщения А. Подставляя уравнение реле f(x)=A sign (x) и выражение для нормальной плотности вероятности (1.17)в соотношения (1.27) — (1.28) и учитывая свойства интеграла вероятно­сти (1.21), получаем

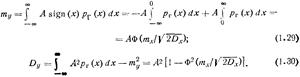
Аналитически решение задачи определения плотности вероятно­сти p(у) нелинейной функции y = f(x) от случайной величины х мо­жет быть получено лишь в том случае, когда существует взаимно однозначное соответствие между х и у, т. е. когда функция f(х) — монотонная.

Пусть f (x) монотонно возрастает. Тогда функция распределения F(y) может быть найдена с помощью соотношения

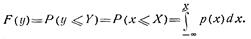
При взаимно однозначном соответствии между х и у из соотноше­ния y=f(x) можно найти обратную функцию 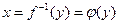поэтому 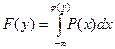. Дифференцирование интеграла по переменной у, входящей в верхний предел, дает

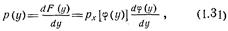
где .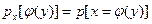

При монотонном убывании f(x)

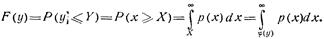
Отсюда

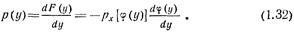
Соотношения (1.31) и (1.32) можно переписать в виде одной фор­мулы:

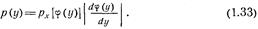
Пример.Пусть 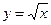, а аргумент х распределен равномерно на интервале [0, 1], т. е.

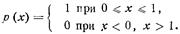
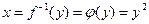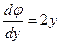Требуется найти p(y). Поскольку в данном , то и

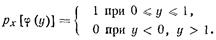
Отсюда

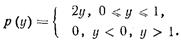
1.1.5. Характеристическая функция и семиинварианты

При решении ряда задач наряду с функцией и плотно­стью распределения вероятностей используют характеристическую функцию случайной величины. Так называют функцию 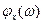, яв­ляющуюся преобразованием Фурье от плотности вероятности:

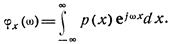
Приведем некоторые свойства характеристических функций

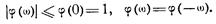
Если 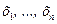— независимые случайные величины и

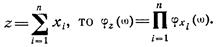
Математическое ожидание и дисперсию случайной величины можно найти, используя производные от логарифма характеристи­ческой функции :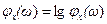

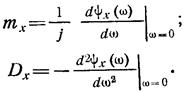
Для гауссовской случайной величины х с математическим ожи­данием т и дисперсией D

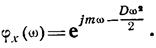
Производную R-го порядка логарифма характеристической функции в точке 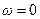, умноженную на 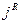, называют семиинвариан­том R-го порядка случайной величины. Первыми двумя семиинвари­антами являются математическое ожидание и дисперсия, а семиин­вариант порядка R есть рациональная функция первых R моментов случайной величины. В частности,

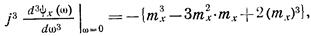
где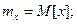

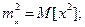
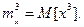
СЛУЧАЙНЫЕ ПРОЦЕССЫ