Элементы комбинаторики. Правило суммы и произведения
Комбинаторика - это раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из элементов, принадлежащих данному множеству.
Решение многих комбинаторных задач основывается на двух фундаментальных правилах, называемых правилом суммы и правилом произведения.
Правило суммы
Если некоторый объект А может быть выбран из совокупности объектов n способами, а другой объект В может быть выбран m способами, то выбрать либо объект А, либо объект В можно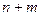 
способами.
Правило произведения
Если объект А может быть выбран из совокупности объектов n способами и посла каждого такого выбора объект В может быть выбран m способами, то пара объектов (А,В) в указанном порядке может быть выбрана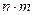 
способами.
Примеры.
7. В первом ящике 8 шаров, во втором -10 шаров. Сколькими способами можно выбрать один шар из двух ящиков?
► Событие А – выбор шара из первого ящика, он может быть осуществлен 8-ю способами, событие В – выбор шара из второго ящика, он может быть осуществлен 10-ю способами, т.е. n=8, m=10. Событие А+В – выбор одного шара либо из первого ящика, либо из второго. По правилу суммы находим: 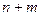=8+10=18.
8. Сколько можно составить пятизначных чисел так, чтобы любые две соседние цифры были различны?
► Первую цифру можно выбрать 9-ю способами, вторую – 9-ю способами и т.д., следовательно, всего цифр можно составить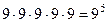 
способами (правило произведения).
Основные формулы комбинаторики
Выборки без повторений
Пусть дано конечное множество X, состоящее из n элементов.
Размещениемиз n элементов по m множества X называют любые наборы, которые отличаются либо составом элементов, либо их порядком:
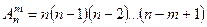. (4)
Частный случай размещения – перестановки: наборы, состоящие из n одних и тех же элементов, отличающиеся только порядком их расположения.
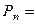n!. (5)
Сочетанием из n элементов по m множества X называют любые неупорядоченные наборы, которые отличаются хотя бы одним элементом:
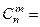
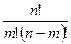. (6)
Отсюда может быть выведена формула размещения, более удобная для счета:
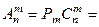
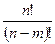. (7)
Примеры.
9. Сколько различных двузначных чисел можно составить из чисел 1,2,3,4?
► 
.
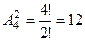10. Сколько различных четырехзначных чисел можно составить из чисел 1,2,3,4?
► 
.
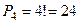11. Сколькими способами можно выбрать две детали из ящика с десятью деталями?
► 
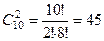
Выборки с повторениями
Перестановки с повторениями – это различные конечные наборы из n элементов, в которых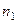 
элементов принадлежат одному виду, 
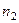элементов – другому виду и т.д. и 
.
= 
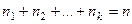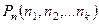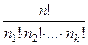. (8)
Пример.
12. Сколько различных шестизначных чисел можно составить из трех единиц, одной двойки и двух троек?
► 
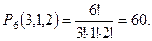
Сочетания с повторениями
Сочетанием из n элементов множества X по m с повторениями называют любые неупорядоченные наборы, состоящие из m элементов, каждый из которых принадлежит к одному из n видов.
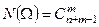(9)
Например, из трех различных элементов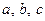 
можно составить следующие сочетания с повторениями: 
.
► 
.
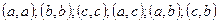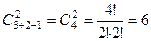Размещения с повторениями
Пусть X – множество из n элементов. Достаем один элемент, фиксируем, кладем элемент обратно. Выборку производим т раз. Число таких наборов из n элементов множества X по m равно
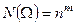. (10)
Пример 13. Сколько существует трехзначных телефонных номеров?
► 
.
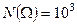Условная вероятность.
Вероятность наступления события А при условии, что В произошло, называется условной вероятностью А при условии В:
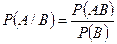, где 
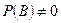. (11)