Алгебраические операции над событиями

Так как случайные события есть множества, то к ним применимы операции пересечения, объединения и дополнения множеств.

Событие, состоящее в наступлении хотя бы одного из событий А или В, называется суммой (объединением) событий А и В и обозначатся А+В (А 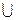В).

Событие, состоящее в наступлении обоих событий А и В, называется произведением (пересечением) этих событий и обозначается АВ ( ).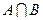

Разностью событий А–В (А\В) называется событие, состоящее из элементов множества А, не принадлежащих В. Оно состоит в том, что А произошло, а В не произошло.

Если А – событие, то противоположным к нему называют событие, обозначающееся 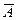и состоящее из тех элементов, которые не принадлежат А; 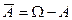, т.е. 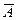происходит в том и только том случае, когда А не происходит. Для противоположных событий одновременно выполняются два условия: а) 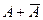- достоверное событие, б) 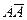- невозможное событие.

Два события называются совместными (несовместными), если в результате их осуществления возможно (или невозможно) их совместное осуществление, т.е. для несовместных событий выполняется: 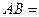Ø.

События 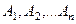называют полной группой несовместных событий, если:

1. 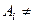Ø для ,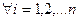

2. 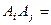Ø для ,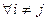

3. .

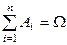Замечание: Операции суммы и произведения аналогично определяются для любого числа событий.

Статистическое, классическое и геометрическое определение вероятности.

Рассмотрим случайный эксперимент с Ω – пространством элементарных исходов и А – случайным событием этого эксперимента. Повторим эксперимент 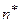раз, предполагая отсутствие влияния результата каждого из проведенных экспериментов на результат другого. Пусть 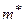- число экспериментов, в которых произошло событие А.

Статистическая вероятность.

Статистической вероятностью (частотой) события А в проведенной серии экспериментов называется число

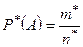. (1)

Свойства:

1. ;

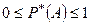2. ;

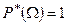3. 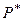(Ø) = 0;

4. если А и В несовместны, то 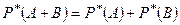(для любого числа событий).

5. 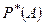обладает свойством устойчивости при 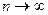, т.е. в различных сериях испытаний при больших п соответствующие частоты 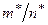практически совпадают, группируясь около некоторого постоянного значения 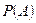, называемого вероятностью.

Классическая вероятность.

Если пространство элементарных событий Ω, соответствующее случайному Э, удовлетворяет условиям:

1. множество Ω конечно: ;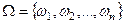

2. все элементарные события равновозможны: ;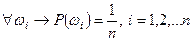

3. элементарные события попарно-несовместны и образуют полную группу событий.

Тогда вероятность любого события можно вычислить по формуле:

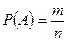, (2)

где n – общее число исходов (событий) испытания; m – число событий, благоприятных событию А.

Свойства:

1. ;

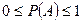2. ;

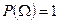3. 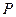(Ø) = 0:

4. если А и В несовместны, то 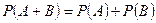(для любого числа событий).

Примеры:

(Пр.5): ,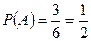

(Пр.6): .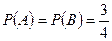

Геометрическая вероятность.

Пусть проведен эксперимент, пространство элементарных исходов которого бесконечно. В этом случае нельзя воспользоваться классическим определением вероятности. В таких случаях вводят понятие геометрической вероятности – обобщение классической вероятности, т.е. вероятность попадания точки в область (отрезок, часть плоской области, часть пространственной области и т.д.)

Пусть 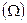- фигура в , .

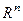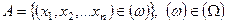Будем считать условия Э такими, что 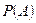не зависит от местоположения 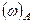в 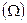и пропорционально мере 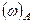. Тогда:

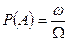, (3)

где 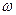- мера фигуры 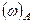, 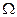- мера фигуры .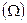