Пространство элементарных событий.

Лекция 1

Пространство элементарных событий.

Предметом теории вероятности являются математические модели случайных экспериментов.

Эксперимент (Э) называют случайным, если заранее нельзя предсказать его результат (исход).

Примеры.

1. Э – бросание одной монеты. Исходы – выпадение герба (Г) или решки (Р). Заранее нельзя предсказать исход.

2. Э – бросание одной игральной кости. Исходы – выпадение 1,2,3,4,5 или 6 очков.

Результаты (исходы) Э называются событиями. События бывают простыми (элементарными) и сложными (составными). Сложные события состоят из простых.

Множество всех возможных взаимоисключающих исходов эксперимента называется пространством элементарных исходов, обозначается Ω. Его элементами являются элементарные исходы, обозначающиеся ω.

Примеры.

3. Э – бросание одной монеты, .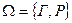

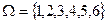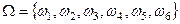4. Э–бросание одной игральной кости, (или , где 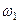- выпадение 1 очка и т.д.)

События обозначаются: А,B,C,…

Элементарные события, принадлежащие событию А, называют благоприятствующими (благоприятными) событию А.

Примеры.

5. Пусть событие А состоит в выпадении четного числа очков при бросании игральной кости. Тогда: 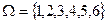, 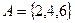(или , ).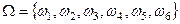

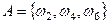6. Монеты подбрасываются дважды. Пусть А – событие, состоящее в том, что хотя бы один раз появится решка, событие В – хотя один раз появится герб. Тогда: , , .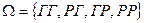

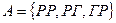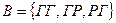Само множество Ω также есть случайное событие, оно называется достоверным, потому что всегда происходит. Пустое множество Ø, не содержащее ни одного элемента, называется невозможным.

Алгебраические операции над событиями

Так как случайные события есть множества, то к ним применимы операции пересечения, объединения и дополнения множеств.

Событие, состоящее в наступлении хотя бы одного из событий А или В, называется суммой (объединением) событий А и В и обозначатся А+В (А 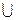В).

Событие, состоящее в наступлении обоих событий А и В, называется произведением (пересечением) этих событий и обозначается АВ ( ).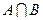

Разностью событий А–В (А\В) называется событие, состоящее из элементов множества А, не принадлежащих В. Оно состоит в том, что А произошло, а В не произошло.

Если А – событие, то противоположным к нему называют событие, обозначающееся 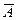и состоящее из тех элементов, которые не принадлежат А; 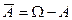, т.е. 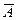происходит в том и только том случае, когда А не происходит. Для противоположных событий одновременно выполняются два условия: а) 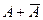- достоверное событие, б) 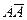- невозможное событие.

Два события называются совместными (несовместными), если в результате их осуществления возможно (или невозможно) их совместное осуществление, т.е. для несовместных событий выполняется: 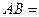Ø.

События 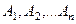называют полной группой несовместных событий, если:

1. 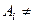Ø для ,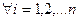

2. 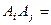Ø для ,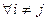

3. .

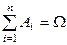Замечание: Операции суммы и произведения аналогично определяются для любого числа событий.

Статистическая вероятность.

Статистической вероятностью (частотой) события А в проведенной серии экспериментов называется число

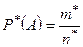. (1)

Свойства:

1. ;

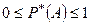2. ;

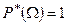3. 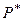(Ø) = 0;

4. если А и В несовместны, то 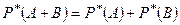(для любого числа событий).

5. 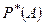обладает свойством устойчивости при 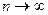, т.е. в различных сериях испытаний при больших п соответствующие частоты 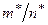практически совпадают, группируясь около некоторого постоянного значения 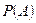, называемого вероятностью.

Классическая вероятность.

Если пространство элементарных событий Ω, соответствующее случайному Э, удовлетворяет условиям:

1. множество Ω конечно: ;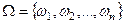

2. все элементарные события равновозможны: ;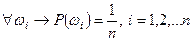

3. элементарные события попарно-несовместны и образуют полную группу событий.

Тогда вероятность любого события можно вычислить по формуле:

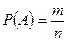, (2)

где n – общее число исходов (событий) испытания; m – число событий, благоприятных событию А.

Свойства:

1. ;

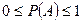2. ;

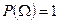3. 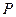(Ø) = 0:

4. если А и В несовместны, то 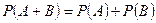(для любого числа событий).

Примеры:

(Пр.5): ,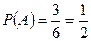

(Пр.6): .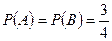

Геометрическая вероятность.

Пусть проведен эксперимент, пространство элементарных исходов которого бесконечно. В этом случае нельзя воспользоваться классическим определением вероятности. В таких случаях вводят понятие геометрической вероятности – обобщение классической вероятности, т.е. вероятность попадания точки в область (отрезок, часть плоской области, часть пространственной области и т.д.)

Пусть 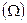- фигура в , .

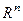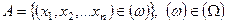Будем считать условия Э такими, что 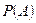не зависит от местоположения 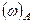в 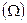и пропорционально мере 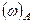. Тогда:

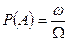, (3)

где 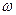- мера фигуры 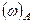, 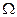- мера фигуры .

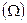Правило суммы

Если некоторый объект А может быть выбран из совокупности объектов n способами, а другой объект В может быть выбран m способами, то выбрать либо объект А, либо объект В можно 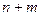способами.

Правило произведения

Если объект А может быть выбран из совокупности объектов n способами и посла каждого такого выбора объект В может быть выбран m способами, то пара объектов (А,В) в указанном порядке может быть выбрана 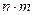способами.

Примеры.

7. В первом ящике 8 шаров, во втором -10 шаров. Сколькими способами можно выбрать один шар из двух ящиков?

► Событие А – выбор шара из первого ящика, он может быть осуществлен 8-ю способами, событие В – выбор шара из второго ящика, он может быть осуществлен 10-ю способами, т.е. n=8, m=10. Событие А+В – выбор одного шара либо из первого ящика, либо из второго. По правилу суммы находим: 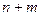=8+10=18.

8. Сколько можно составить пятизначных чисел так, чтобы любые две соседние цифры были различны?

► Первую цифру можно выбрать 9-ю способами, вторую – 9-ю способами и т.д., следовательно, всего цифр можно составить 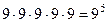способами (правило произведения).

Выборки без повторений

Пусть дано конечное множество X, состоящее из n элементов.

Размещениемиз n элементов по m множества X называют любые наборы, которые отличаются либо составом элементов, либо их порядком:

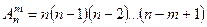. (4)

Частный случай размещения – перестановки: наборы, состоящие из n одних и тех же элементов, отличающиеся только порядком их расположения.

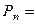n!. (5)

Сочетанием из n элементов по m множества X называют любые неупорядоченные наборы, которые отличаются хотя бы одним элементом:

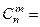
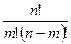. (6)

Отсюда может быть выведена формула размещения, более удобная для счета:

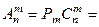
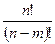. (7)

Примеры.

9. Сколько различных двузначных чисел можно составить из чисел 1,2,3,4?

► .

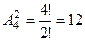10. Сколько различных четырехзначных чисел можно составить из чисел 1,2,3,4?

► .

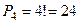11. Сколькими способами можно выбрать две детали из ящика с десятью деталями?

►

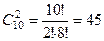
Выборки с повторениями

Перестановки с повторениями – это различные конечные наборы из n элементов, в которых 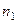элементов принадлежат одному виду, 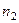элементов – другому виду и т.д. и .

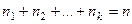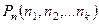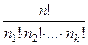= . (8)

Пример.

12. Сколько различных шестизначных чисел можно составить из трех единиц, одной двойки и двух троек?

►

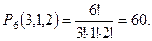
Сочетания с повторениями

Сочетанием из n элементов множества X по m с повторениями называют любые неупорядоченные наборы, состоящие из m элементов, каждый из которых принадлежит к одному из n видов.

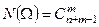(9)

Например, из трех различных элементов 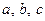можно составить следующие сочетания с повторениями: .

► .

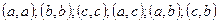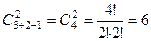Размещения с повторениями

Пусть X – множество из n элементов. Достаем один элемент, фиксируем, кладем элемент обратно. Выборку производим т раз. Число таких наборов из n элементов множества X по m равно

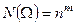. (10)

Пример 13. Сколько существует трехзначных телефонных номеров?

► .

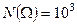Условная вероятность.

Вероятность наступления события А при условии, что В произошло, называется условной вероятностью А при условии В:

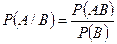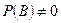, где . (11)

Независимость событий

Если события А и В таковы, что 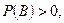то существует условная вероятность 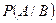. В случае когда

, (*)

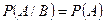мы говорим, что событие А не зависит от события В.

Если и 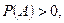то

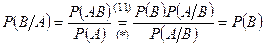, (14)

и из независимости А от В следует независимость В от А, т.е. понятие зависимости А и В симметрично и из формулы умножения вероятностей (12) следует, что для независимости событий А и В имеет место равенство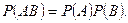

События А и В называются независимыми, если выполнено равенство:

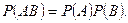(15)

Формула полной вероятности

Если события 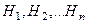образуют полную группу событий и 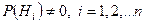, то для любого события А имеет место формула

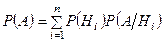, (17)

где события 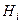называются гипотезами.

Доказательство:

Т.к. 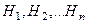образуют полную группу событий, то событие A можно представить как:

,

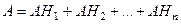где события 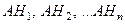попарно несовместны.

Используя свойство аддитивности вероятности и формулу умножения вероятностей, получим:

.

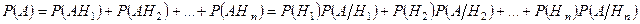Формула Байеса

Если события 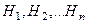образует полную группу событий, то для любого события А, для которого 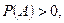справедлива формула:

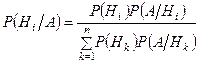- (18)

Доказательство:

По определению условной вероятности и, используя формулу умножения вероятностей, имеем:

.

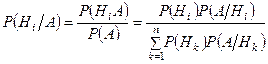Формула Байеса используется в ситуации, когда эксперимент уже проведён, событие А наступило, и требуется переоценить шансы наступления гипотез 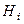, т.е. найти условные вероятности 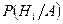. Эти вероятности называются апостериорными (послеопытными), а гипотезы, которые рассматриваются до эксперимента – априорными (доопытными), при этом:

; .

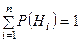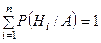Лекция 1

Пространство элементарных событий.

Предметом теории вероятности являются математические модели случайных экспериментов.

Эксперимент (Э) называют случайным, если заранее нельзя предсказать его результат (исход).

Примеры.

1. Э – бросание одной монеты. Исходы – выпадение герба (Г) или решки (Р). Заранее нельзя предсказать исход.

2. Э – бросание одной игральной кости. Исходы – выпадение 1,2,3,4,5 или 6 очков.

Результаты (исходы) Э называются событиями. События бывают простыми (элементарными) и сложными (составными). Сложные события состоят из простых.

Множество всех возможных взаимоисключающих исходов эксперимента называется пространством элементарных исходов, обозначается Ω. Его элементами являются элементарные исходы, обозначающиеся ω.

Примеры.

3. Э – бросание одной монеты, .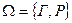

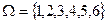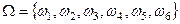4. Э–бросание одной игральной кости, (или , где 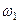- выпадение 1 очка и т.д.)

События обозначаются: А,B,C,…

Элементарные события, принадлежащие событию А, называют благоприятствующими (благоприятными) событию А.

Примеры.

5. Пусть событие А состоит в выпадении четного числа очков при бросании игральной кости. Тогда: 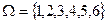, 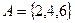(или , ).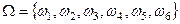

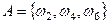6. Монеты подбрасываются дважды. Пусть А – событие, состоящее в том, что хотя бы один раз появится решка, событие В – хотя один раз появится герб. Тогда: , , .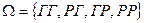

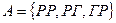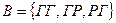Само множество Ω также есть случайное событие, оно называется достоверным, потому что всегда происходит. Пустое множество Ø, не содержащее ни одного элемента, называется невозможным.