Вычисление пропускной способности канала со стиранием

Приемное устройство на основе анализа реализации принятого сигнала выносит решение о том, какая буква (сообщение) была передана. В некоторых случаях создается такая помеховая обстановка, что вынести решение в пользу той или иной буквы не представляется возможным. В этом случае целесообразнее вообще не принимать решение о том, какая буква была передана. Указанный отказ от решения q является тоже решением и входит в множество решений наравне со всеми остальными решениями. Вынужденный отказ от решения часто возникает в проводных каналах связи при нарушении контакта (обрыве). В этом случае сигнал просто не проходит на выход канала и мы вынуждены отказаться от принятия решения даже в случае отсутствия внешних помех.

Вычислим пропускную способность канала, диаграмма переходных вероятностей которого изображена на рис. 4.5 .

1-Pe-PΘ

1-Pe-PΘ

P

x1

1-P

x2

Θ

Y1

Y2

PΘ

Pe

PΘ

Pe

Рис. 4.5. Диаграмма переходных вероятностей для канала со стиранием

Указанный канал описывается матрицей:

.

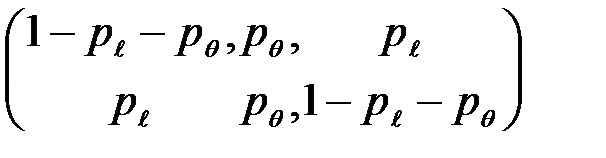Поскольку строки матрицы различаются только перестановкой чисел 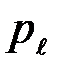, , 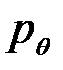, 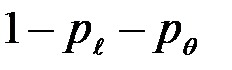то соответствующий канал симметричен по входу.

Для симметричного по входу канала условная энтропия

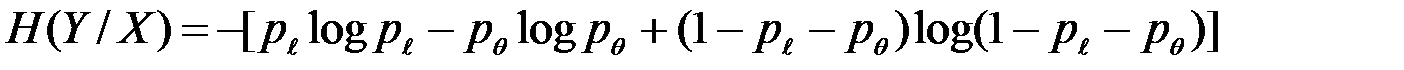(4.8)

не зависит от вида распределения источника сообщений и полностью определяется параметрами канала 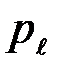и .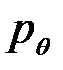

Поэтому пропускная способность канала можно записать в виде

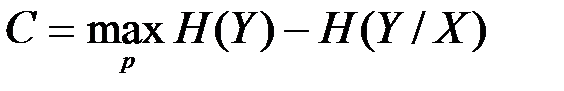(4.9)

Вычислим , энтропия определяется через вероятности:

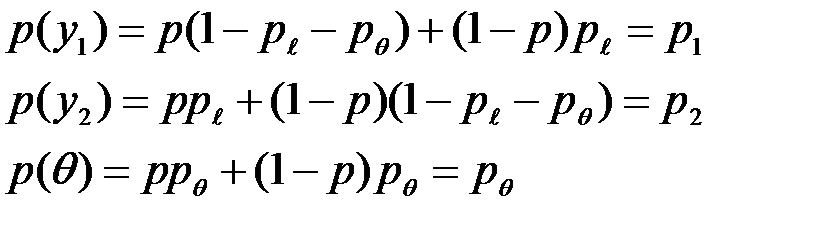
где обозначения 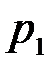и 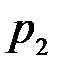введены для сокращения записи. Из последнего равенства следует, что безусловная вероятность 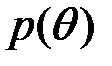равна условной вероятности .

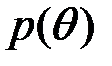Принимая во внимание, что 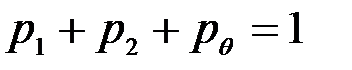, имеем:

= =

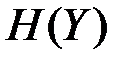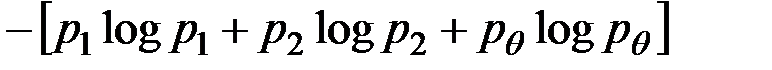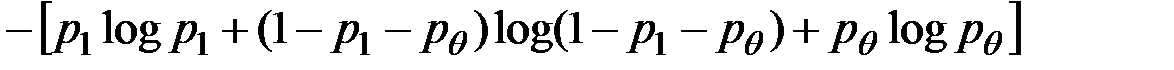
Отсюда следует, что 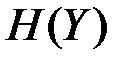зависит от 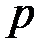(от распределения источника) только через .

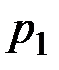Значение 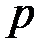, при котором 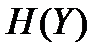достигает своего максимального значения, определяется из уравнения ,

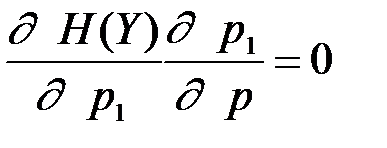которое для данного случая имеет вид: .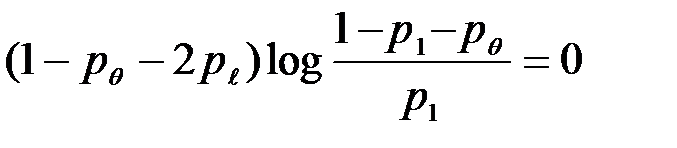

Последнее уравнение распадается на два уравнения:

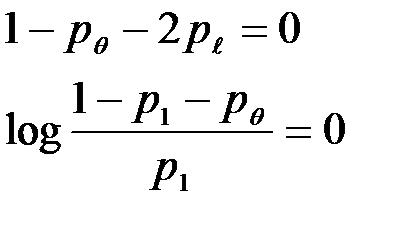
Если параметры канала 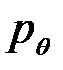и 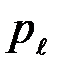удовлетворяют первому уравнению, то есть 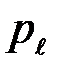=0.5 (1- 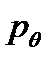), то пропускная способность канала 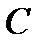= 0. При этом 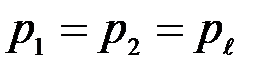независимо от значения вероятности .

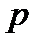ПОМЕХОУСТОЙЧИВОЕ КОДИРОВАНИЕ

Теоремы К. Шеннона

Появление теории помехоустойчивого кодирования было вызвано необходимостью обеспечения надёжной передачи сообщений при наличии помех, которые всегда существуют в реальных системах.

Рассмотрим наипростейший способ повышения надёжности передачи сообщений посредством многократной передачи одного и того же сообщения.

Пусть по каналу связи каждое из сообщений x₁=1 и x₂=0, образующих множество Х, передаётся по три раза. Тогда передачу сообщения x₁=1 (x₂=0) можно рассматривать как передачу по каналу связи соответствующего кодового слова 111= 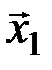(000= 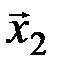). Число различных последовательностей, которые при этом могут появиться на выходе канала связи, равно 2³=8. Они образуют множество 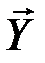, которое назовём множеством выходных последовательностей. Кодовые слова 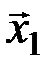и 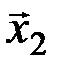также можно считать принадлежащими некоторому множеству Х, которое назовём множеством входных канальных последовательностей. Оно состоит из 2³ последовательностей.

Для отображения характера взаимодействия помехи и сигнала вводится модель канала связи, с помощью которой устанавливается связь между передаваемой последовательностью 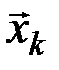и принимаемой последовательностью 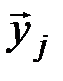в виде:

,

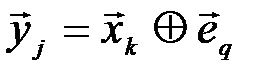где 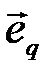- вектор ошибок, который представляет собой последовательность нулей и единиц. Единица указывает место, где произошла ошибка, а ноль указывает на отсутствие ошибки. Суммирование производится по модулю два.

Пусть в канале действует единичная ошибка, т.е. вектор 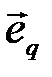может содержать только одну единицу. Из-за единичной ошибки кодовое слово 111= 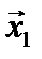(000= 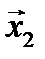) может перейти в такие кодовые слова множества Y, которые содержат один ноль (два нуля), что позволяет безошибочно определить, какое кодовое слово было передано, а, следовательно, и передаваемое сообщение. Таким образом, множество 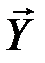делится на два непересекающихся подмножества, которые находятся во взаимно однозначном соответствии с сообщениям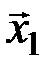и и .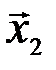

Последовательности множества , подлежащие передаче, называются разрешёнными, а все остальные – запрещёнными. Кодирование, в сущности, сводится к разбиению множества X на разрешённые и запрещённые последовательности (кодовые слова). Часто кодом называют множество разрешённых кодовых слов. Выбор разрешённых кодовых слов (выбор кода) определяет верность передачи сообщений.

Таким образом, верность передачи сообщения можно повысить за счёт увеличения числа повторений, т.е., за счёт существенного снижения скорости передачи информации. В рассматриваемом случае скорость передачи информации уменьшилась в три раза за счёт трёхкратного повторения. Однако в некоторых условиях ошибку декодирования можно сделать сколь угодно малой посредством выбора соответствующего кода, если производительность источника будет меньше пропускной способности канала на любую сколь угодно малую величину. Существование такого способа кодирования (кода) было доказано К. Шенноном и сформулировано им в виде следующих теорем:

Теорема 1. Если производительность источника Н_u меньше пропускной способности канала С, то существует такой код и способ декодирования, при которых возможна передача сообщений со сколь угодно малой вероятностью ошибки, при неограниченном возрастании длины последовательности n.

Теорема доказывается при следующей мысленной организации способа передачи сообщений. Подлежащие передаче сообщения представляют собой последовательность символов, которые вырабатывает, в общем случае, марковский источник сообщений, производительность которого равна Н_u. При неограниченном увеличении длины последовательности n источник вырабатывает с вероятностью, равной единице, типичные последовательности, количество которых равно 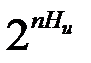. Будем передавать только типичные последовательности (сообщения), а нетипичные последовательности вообще не будем передавать, соглашаясь с тем фактом, что в случае передачи нетипичной последовательности всегда имеет место ошибка.

Таким образом, вероятность появления ошибки равна вероятности появления нетипичной последовательности и стремится к нуля при неограниченном увеличении n.

Специальный «генератор», производительность которого равна Н(Х’), вырабатывает входные канальные последовательности из n независимых символов. Используются не все, а только типичные входные канальные последовательности, количество которых равно 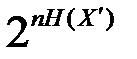. Нетипичные последовательности нет смысла использовать, поскольку они появляются с вероятностью равной нулю, при неограниченном увеличении n. Множество Х’_T входных типичных последовательностей разбивается на разрешённые и запрещённые последовательности. Кодирование осуществляется посредством установления взаимно однозначного соответствия между разрешёнными последовательностями и типичными последовательностями, которые вырабатывает источник сообщений.

В теореме утверждается, что при H_и < C= Н(Х’) - Н(Х’/Y) существует такое разбиение множества Х’_T на разрешённые и запрещённые последовательности (существует такой код), при котором вероятность ошибки будет меньше любой сколь угодно малой наперёд заданной величины, если выбрать достаточно большую длину последовательности n. Докажем, что условие H_и < C является необходимым для передачи сообщения со сколь угодно малой вероятностью ошибки.

С позиций внешнего наблюдателя передающую и приёмную части можно рассматривать как одну сложную схему, а передачу отдельного символа, как реализацию некоторого состояния (x_i, y_j) сложной системы.

Если количество переданных и принятых символов n достаточно велико, то с вероятностью, близкой к единице, будут появляться типичные последовательност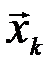и и 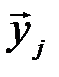и типичные последовательности состояний сложной системы ( 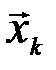, 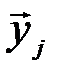), количество которых соответственно равно:

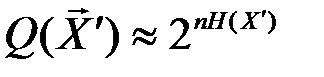
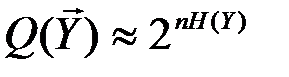
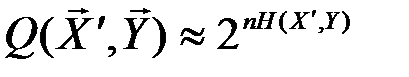
Указанные множества типичных последовательностей обозначим, соответственно, через X’_T, Y’_T, (X’, Y)_Т. С учётом равенства

Н(Х’, Y) = Н(Y) + Н(X’/Y),

количество типичных последовательностей:

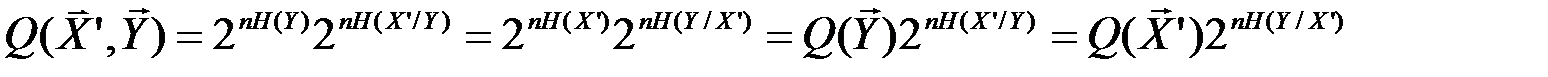(4.10)

Если множества Х’ и Y статистически независимы, то

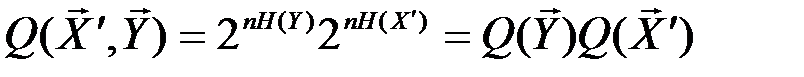
Наличие статистической зависимости между множествами Х’ и Y уменьшает число типичных последовательностей Q(X’,Y), поскольку всегда

H(X’) > H(X’/Y) и H(Y) > H(Y/X’).

Таким образом, в образовании типичной последовательности ( 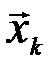, 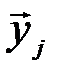) 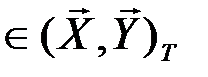состояний сложной системы могут участвовать все типичные последовательност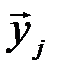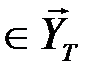и и 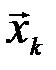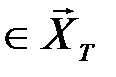, но не во всех сочетаниях (рис. 4.6).

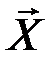Рис. 4.6. Вероятностная диаграмма, описывающая модели системы связи К. Шеннона

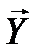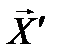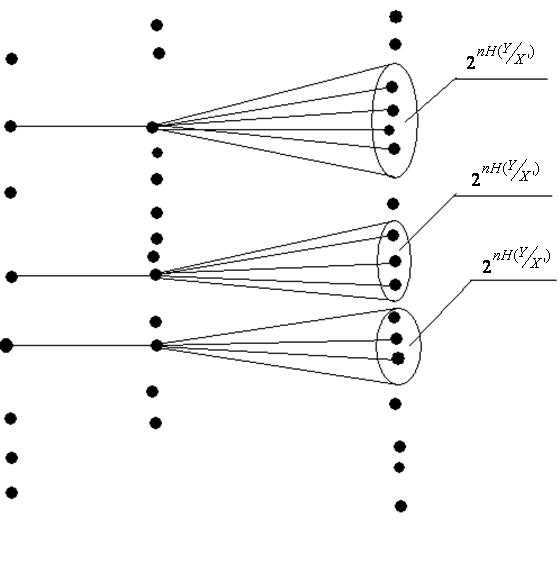
Обозначим через Q( ) число типичных последовательностей 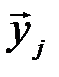, которые в сочетании с типичной последовательностью 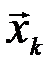могут образовывать типичные последовательности ( 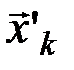, 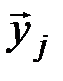). Тогда общее число типичных последовательностей

.

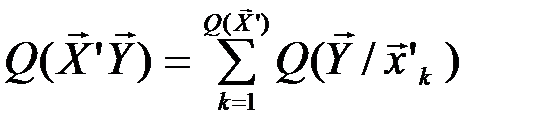Можно доказать, что 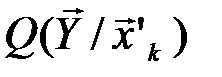не зависит от номера типичной последовательности k. Поэтому (последнее равенство) можно переписать в виде:

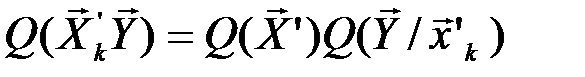
Отсюда с учётом (4.10) получим

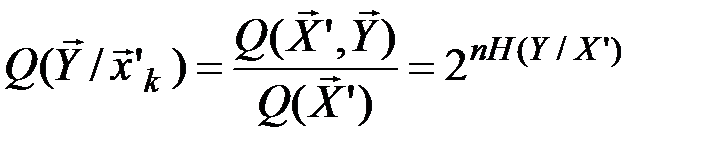
В результате аналогичных рассуждений можно получить, что

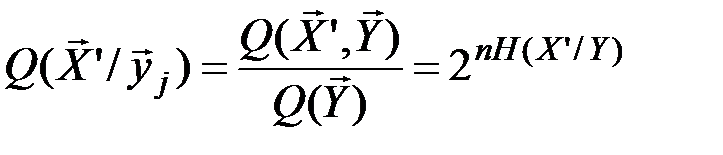
Таким образом, при передаче входной канальной последовательности 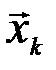с вероятностью, равной единице, будет принята последовательность 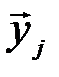, принадлежащая подмножеству 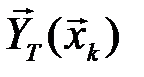, содержащему 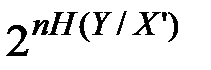последовательностей. Аналогично, если была принята последовательность 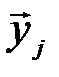, то с вероятностью, близкой к единице, была передана последовательность 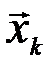, принадлежащая подмножеству 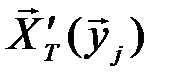, содержащему 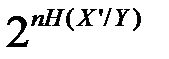последовательностей (рис. 4.6). Декодирование с вероятностью, равной единице, будет безошибочным только в том случае, если разрешённые последовательности набирать таким образом, чтобы соответствующие подмножества 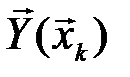не пересекались. Максимальное количество непересекающихся подмножеств равно

,

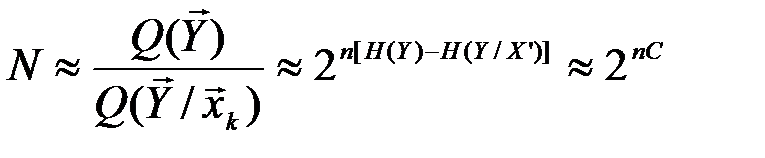где пропускная способность канала

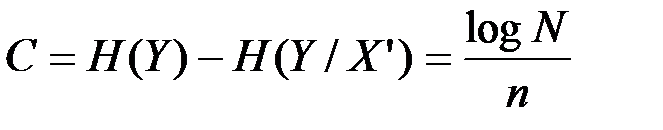
определяется максимальным количеством канальных последовательностей N (разрешённых последовательностей), которые безошибочно могут быть переданы по каналу связи. Очевидно, количество типичных последовательностей, которые вырабатывает источник сообщений должно быть меньше N:

.

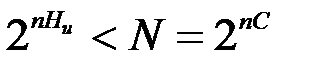Отсюда Н_и < C.

Теорема 2. Если Н_и < C, то среди кодов, обеспечивающих сколь угодно малую вероятность ошибки, существует код, при котором скорость передачи информации R сколь угодно близка к скорости создания информации .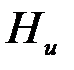

Идея доказательства состоит в следующем. Скорость передачи информации ( на символ ) определяется как

,

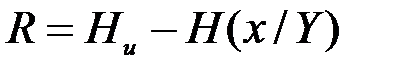где 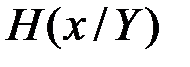- апостериорная энтропия переданного сообщения на символ, или количество рассеянной в канале информации. Доказывается, что энтропия 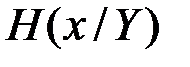может быть меньше сколь угодно малой величины, если выбрать достаточно большое значение n . Отсюда следует, что R сколь угодно мало отличается от 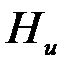при неограниченном увеличении n.

Из теоремы следует, что C можно интерпретировать как предельную скорость передачи информации, при которой можно получить вероятность ошибки.

Теорема 3. (Обратная теорема).

Если скорость создания информации 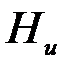больше пропускной способности канала C, то никакой код не может обеспечить сколь угодно малую вероятность ошибки. Минимальное рассеяние информации на символ, достижимое при 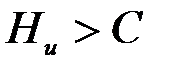, равно 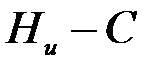; никакой код не может обеспечить меньшего рассеяния информации.

В теоремах не затрагиваются вопросы построения оптимального кода. Тем не менее, значение их огромно, поскольку, обосновав принципиальную возможность такого кодирования, они мобилизовали усилия ученых на разработку конкретных кодов.