Моделирование случайных величин

Описание законов распределения вероятностей случайных величин осуществляется при помощи функции распределения (интегральной функции распределения) или плотности распределения вероятностей , которые связаны между собой соотношениями:

; .

Напомним, что функция распределения вероятностей в точке рана вероятности наступления события: «Значение в результате реализации случайной величины 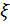оказалось строго меньше значения »[1]:

.

Плотность распределения вероятностей характеризует вероятность попадания значения случайной величины в ту или иную область оси абсцисс. Вероятность попадания реализации аналоговой случайной величины в точку, очевидно, равна нулю, вероятность же попадания в интервал [a,b] (пусть сколь угодно малый), имеет определенную величину[2]. С учетом определения плотности распределения вероятностей запишем:

.

Включение или не включение конечных точек в интервал интегрирования несущественно в силу сказанного ранее.

Датчики (генераторы) случайных (псевдослучайных) чисел с заданным законом распределения вероятностей, т. е. с заданной функцией плотности распределения вероятностей W(x) либо интегральной функцией распределения применяются исключительно широко в криптографии, стеганографии, при математическом (имитационном) моделировании сложных технических систем, при реализации компьютерных игр и т.д. Особенно часто необходимость в подобных датчиках возникает при исследовании или проектировании информационных систем, систем массового обслуживания.

Существует три способа получения реализаций последовательностей случайных чисел:

· выбор из таблиц случайных чисел (неудобство этого метода достаточно очевидно);

· использование физических датчиков (что также является сложной задачей, поскольку для каждого закона распределения потребуется изготовление собственного физического датчика; кроме того, в задачах защиты информации часто требуются псевдослучайные числа, а физические датчики обычно являются генераторами случайных чисел);

· генерирование псевдослучайных последовательностей чисел на ЭВМ.

Специфика всякой решаемой задачи защиты информации или моделирования требует своего закона распределения случайной величины, т.е. своей функции W(x) либо F(х). Разрабатывать датчики случайных чисел "на все случаи жизни" нерационально и практически невозможно. Отсюда необходимость создания некоторого универсального, простого в реализации генератора случайных чисел с достаточно простым законом распределения, используя который можно было бы получать случайные числа с законом распределения вероятностей, соответствующим решаемой задаче. В качестве такого генератора чаще всего используется датчик псевдослучайных чисел, равномерно распределенных в диапазоне (0, 1), реализуемый программно на ЭВМ.

Существуют три группы методов генерации случайных чисел с заданным законом распределения с использованием последовательности случайных чисел, равномерно распределенных в диапазоне (0,1):

1) точные — методы нелинейного преобразования и метод Неймана;

2) приближенные — метод кусочной аппроксимации, метод замены непрерывных распределений соответствующими дискретностями, метод численного решения уравнения при нелинейном преобразовании;

3) специальные — методы, основанные на свойствах преобразований случайных величин.

2.1. Моделирование случайной величины с произвольно заданным законом распределения посредством нелинейного преобразования случайной величины с равномерным законом распределения

Имеется датчик случайной (псевдослучайной) величины Y с функцией распределения вероятностей, равномерной в диапазоне [0,1],

(2.1)

Требуется получить датчик случайных чисел х с иным законом распределения вероятностей. Предполагается, что необходимый закон распределения известен точно, т.е. аналитическое выражение требуемой плотности распределения вероятностей W(х) либо функции распределения F(х) задано.

Рис. 2.1. Преобразование равномерно распределенной в диапазоне (0,1) случайной величины y в случайную величину x с интегральной функцией распределения F(x)

Решение поставленной задачи сводится к определению вида нелинейного преобразования x=g(y) (рис.2.1) случайной величины Y с равномерным на интервале (0,1) законом распределения, в результате которого получается случайная величина X с заданной плотностью распределения вероятностей W(x). Вероятность того, что реализация случайной величины y попадет в интервал dy, равна вероятности того, что значение x=g(y) попадет в соответствующий интервал dx:

W(y)dy=W(x)dx.

Поскольку случайная величина y имеет равномерный закон распределения, то W(y)=1 во всей области определения [0,1]. Поэтому dy=W(x)dx. Интегрируя это дифференциальное уравнение, получим

. (2.2)

Графическая иллюстрация проделанных преобразований приведена на рис.2.1.

В результате решения уравнения (2.2) относительно переменной х можно определить вид функции g(y), которая совпадает с функцией, обратной к интегральной функции распределения F(х): .

Пример. Пусть требуется получить случайную величину с релеевским законом распределения, у которой

F(х)=1-exp(-x²/2σ²), W(x)=(x/ σ²) exp(-x²/2 σ²).

Тогда, решая уравнение у=1-ехр(-х²/2σ²), получим х= σ .

Известно, что если случайная величина у распределена равномерно в диапазоне [0,1], то случайная величина 1-у имеет такой же закон распределения, поэтому последнее равенство целесообразно заменить статистически эквивалентным: x=g(у)= σ . Таким образом, если датчик генерирует последовательность случайных чисел у_i, i = 1, 2..., с равномерным законом распределения, то последовательность чисел x_i= σ i=1, 2... будет иметь закон распределения Релея.

Метод Неймана

Случайную величину с заданной плотностью распределения вероятностей W(x) можно получить из базовой последовательности случайных (псевдослучайных) чисел имеющих равномерную плотность распределения вероятностей на интервале [0,1] следующим образом.

Пусть имеются две случайные величины X, и Y, с равномерными законами распределения, которые образуют двумерное пространство элементарных событий (рис.2.2).

Рис.2.2 Двумерное пространство элементарных событий:

B – область в пространстве элементарных событий между осью абсцисс и кривой, воспроизводящей в некотором масштабе плотность распределения вероятностей W(x); a - область прямоугольника с размерами: dx – по оси абсцисс, b - по оси ординат

Случайные величины X и Y можно получить в результате умножения чисел базовой последовательности соответственно на a и b. Функция f(x) изображает в общем случае в произвольном масштабе заданную плотность распределения вероятностей W(x). Буквой a будем обозначать область прямоугольника с размерами: по оси абсцисс – dx, по оси ординат – b; B – область в пространстве элементарных событий между осью абсцисс и кривой f(x).

Алгоритм

1. На первом шаге вырабатываются реализации x₁ и y₁ случайных величин X и Y (точка в пространстве элементарных событий).

2. Если точка с координатами (x₁,y₁)попала в область B под функцией f(x), то y₁ отбрасывается, а x₁ используется в качестве выходного значения случайной величины. В противном случае отбрасываются оба значения x₁ и y₁ (холостой прогон).

3. Переход к пункту 1.

Таким образом, случайная величина с плотностью распределения W(x)формируется посредством прореживания базовой последовательности.

Докажем, что получаемая таким образом случайная величина описывается плотностью распределения вероятностей W(x),которая совпадает в определенном масштабе с функцией f(x). В данном случае вероятность W(x)dx попадания реализации выходной случайной величины в интервал dx равна условной вероятности P(A/B)=P(AB)/P(B)=W(x)dx, где события A и B определены как подмножества в пространстве элементарных событий. Поскольку плотность распределения вероятностей постоянна в пространстве элементарных событий, то применим геометрический метод вычисления вероятностей, т.е. условная вероятность P(A/B) равна отношению площади пересечения событий A и B к площади S(B) события B: W(x)dx= P(A/B)=f(x)dx / S(B).

Отсюда следует, что W(x) = f(x)/ S(B).

2.3. Моделирование случайной величины в случае приближенного задания ее закона распределения

Если аналитическое выражение нелинейного преобразования x=q(y) не удается получить, или оно имеет сложный, "громоздкий" вид, а также, если распределение случайной величины X точно не известно, в задачах моделирования применяют аппроксимацию. Пусть требуется получить случайную величину X с плотностью распределения вероятностей W(x).

Аппроксимацию можно реализовать с помощью конечного ряда

W(x) ≈ P_1.w₁(x)+P_.iw_i(x)+P_nw_n(x)=Ŵ(x), (2.3)

где w_i(x), i=1…n – законы распределения вероятностей n независимых случайных величин; P_i. – коэффициенты разложения; Ŵ(x) – результат аппроксимации требуемой плотности распределения вероятностей. Точность аппроксимации обычно выбирается экспериментально, хотя можно использовать и теорию разложения функции в ряды. Проектируемый программный модуль (генератор) должен вырабатывать псевдослучайную величину с плотностью распределения Ŵ(x).

Блок-схема алгоритма генерации случайной величины с плотностью распределения Ŵ(x)представлена на рис.2.3.

Рис.2.3 Блок-схема алгоритма генерирования случайной величины

с плотностью распределения Ŵ(x)

На первом шаге с вероятностью P_i выбирается один из генераторов случайных величин с плотностью распределения вероятностей _.w_i(x), i=1…n.

На втором шаге выбранный генератор вырабатывает реализацию x случайной величины X, которая используется как выходная.

Докажем, что на выходе получаем случайную величину с законом распределения вероятностей, равной Ŵ(x). Вероятность Ŵ(x)dx вычисляется по формуле полной вероятности Ŵ(x)dx = P_1.w₁(x),dx+ …+P_i.w_i(x)dx +…+ P_nw_n(x)dx, где _.w_i(x)dx – интерпретируется как условная вероятность попадания реализации случайной величины X в интервал dx при условии, что выбран генератор с плотностью распределения вероятностей w_i(x).

Обычно плотности w_i(x)принадлежат одному типу и различаются только средними значениями и (при необходимости) – дисперсией.