Формула полной вероятности и формула Байеса

В принципе, все вероятности событий являются условными, поскольку все события происходят при том или ином комплексе условий. Тем не менее, любой комплекс условий, который реализуется в данном эксперименте, можно считать полным начальным, т.е. без каких-либо ограничений, а соответствующие вероятности событий - полными или безусловными.

Часто полный комплекс условий можно представить как совокупность частных комплексов условий, которые образуют некоторую вероятностную структуру. Тогда вероятность некоторого события 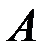при частном комплексе условий можно назвать частной или условной вероятностью.

Рассмотрим следующий способ вероятностной организации совокупности комплексов условий. Пусть имеется 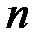комплексов условий, каждый из которых реализуется в данном эксперименте с некоторой вероятностью 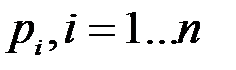. Реализацию некоторого частного комплекса условий будем интерпретировать как появление события 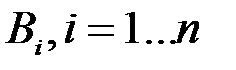с вероятностью, равной 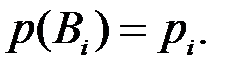Все события 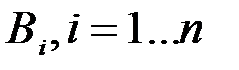образуют полную группу несовместных событий. Требуется вычислить полную вероятность события 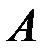, которое может наступить лишь при появлении одного из событий 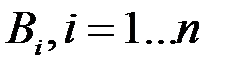с известной условной вероятностью 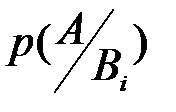и при известных вероятностях 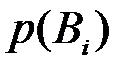. 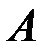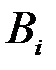Для событий и можно записать формулу умножения вероятностей в виде

.

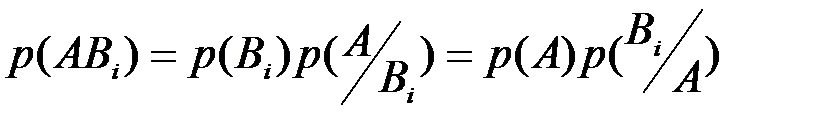Тогда полная вероятность

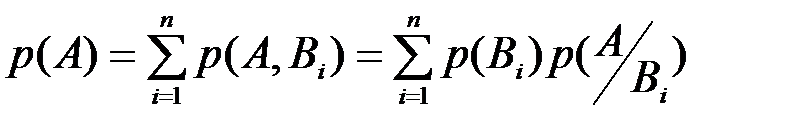
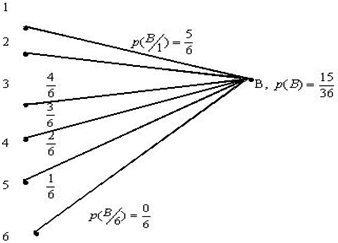
получается в результате суммирования двухмерного закона распределения по всем событиям , которые требуется исключить, т.е. понизить размерность распределения. Полученное выражение для вычисления вероятности 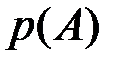называется формулой полной вероятности, геометрическая интерпретация которой представлена в виде вероятностной диаграммы (Рис. 1.4). Вероятность 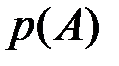равна сумме произведений вероятностей 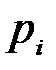на условные вероятности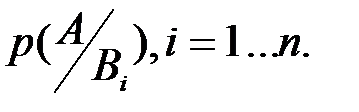

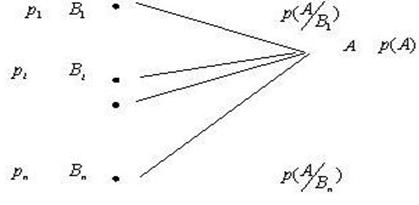
Рис.1.4. Вероятностная диаграмма

Из формулы умножения вероятностей следует, что

.

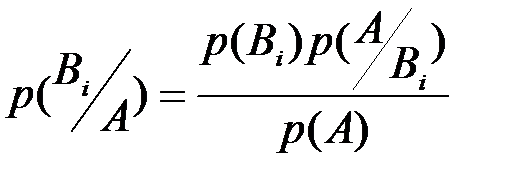Полученное выражение называется формулой Байеса, где 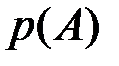вычисляется по формуле полной вероятности.

Формула Байеса позволяет вычислить вероятность события 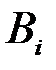при условии, что появилось событие 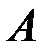. В этом случае события 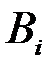называются гипотезами и, как правило, обозначаются через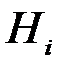 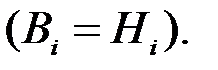Можно дать следующую интерпретацию формулы Байеса. В результате опыта реализуется ненаблюдаемое событие 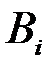с априорной (доопытной) вероятностью, равной 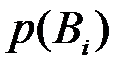, и наблюдаемое событие 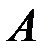, которое доставляет некоторое количество информации о реализованном событии 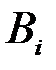. На основании полученной информации вероятности 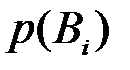могут быть переоценены по формуле Байеса, т.е. может быть вычислена апостериорная (послеопытная) вероятность 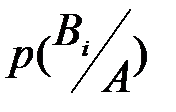события .

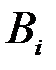Задача. Выше была задача про студента, который выучил 10 билетов из 25. Требовалось определить, в каком случае вероятность вынуть выученный билет больше, когда студент вынимает билет первым или вторым (билеты не возвращаются)? Задача была решена общим стандартным методом с построением полного пространства элементарных событий (рис. 1.2). Однако ее можно решить и с использованием формулы полной вероятности. Вероятностная диаграмма для этой задачи изображена на рис.5, где события 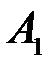и 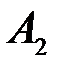состоят в том, что был вынут выученный билет соответственно при первом и втором вынимании билета; событие 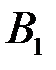- вынут невыученный билет при первом вынимании.

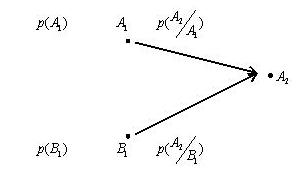
Рис.1.5. Вероятностная диаграмма

События 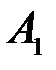и 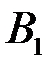образуют полную группу несовместных событий 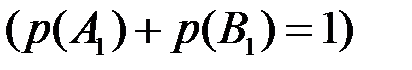. Вероятность 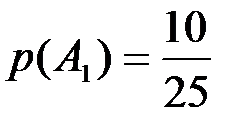вычисляется классическим методом, а вероятность 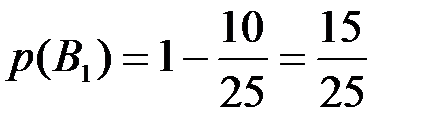. Условные вероятности вычисляются следующим образом. Появление события 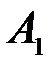изменяет комплекс условий, при котором наступает событие 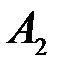, а именно: количество выученных билетов уменьшается до 9, а общее количество билетов уменьшается до 24, отсюда 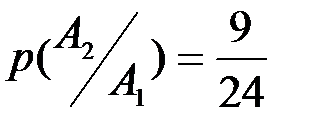. Аналогично вычисляется вероятность 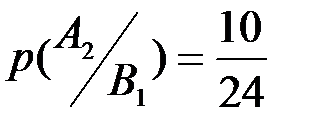. По формуле полной вероятности вероятность 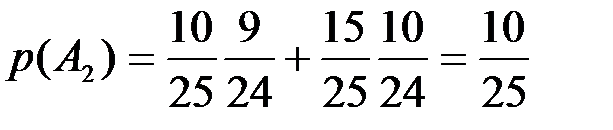. Отсюда следует, что .

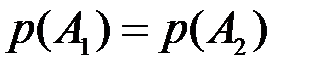Задача. Выше была решена классическим методом следующая задача. Кубик бросают два раза. С какой вероятностью при первом испытании появится единица (событие 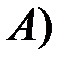при условии, что при втором испытании выпало значение больше, чем при первом (событие ).

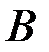Пространство элементарных событий для этой задачи изображено на рис.1.6. Эту задачу можно решить по формуле Байеса без построения полного пространства элементарных событий. В этом случае следует использовать вероятностную диаграмму.

Рис.1.6. Вероятностная диаграмма

Слева изображены цифры, образующие пространство элементарных событий для первого кубика. Все события равновероятны 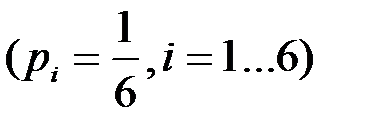. Условная вероятность 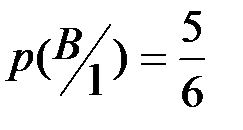события 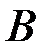вычисляется как вероятность того, что при втором испытании выпадет значение больше 1. Аналогично вычисляются остальные условные вероятности. По формуле полной вероятности находим:

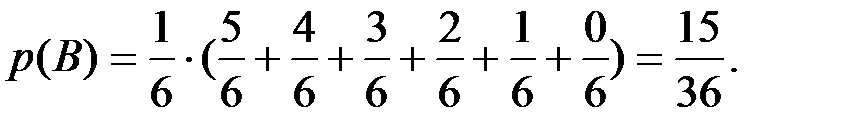
Условная вероятность 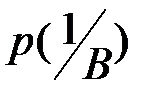вычисляется по формуле Байеса: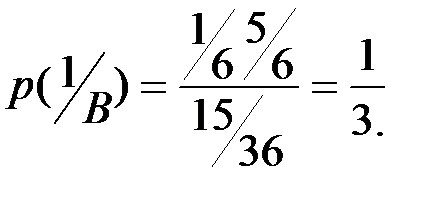

Задача. Рассмотрим пример оценки условной вероятности в случае непрерывной случайной величины. Мишень в виде круга радиуса 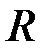можно рассматривать как пространство элементарных событий , если вероятность попасть в мишень принять равной единице (полная группа событий). Кроме этого, события можно считать несовместными, если размеры пули считать бесконечно малой величиной.

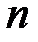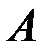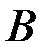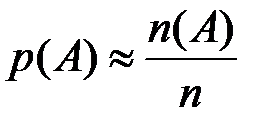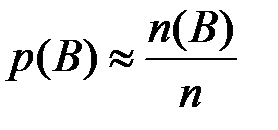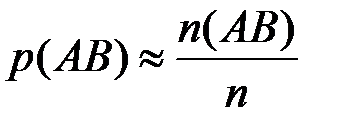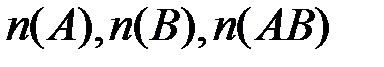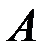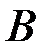Стрелок делает выстрелов, целясь в центр мишени, при этом пули будут распределены по всей мишени с некоторой плотностью, которую можно измерять количеством пуль (или весом пуль, поскольку все пули имеют одинаковый вес) приходящим на единицу площади. Выделим в мишени две фигуры (события) и , и оценим вероятности их поражения. Очевидно, , , , где -количество пуль, попавших соответственно в , в и в 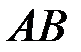- пересечение событи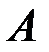й и 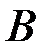. В частности, значение вероятности можно интерпретировать как вес соответствующего события по отношению к весу всего пространства , равному .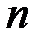

Кроме этого, можно ввести условную вероятность 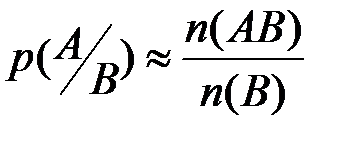, т.е. вес события 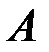, которое появляется вместе с 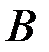(вес пересечения 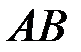) по отношению к весу события 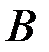. Аналогично .

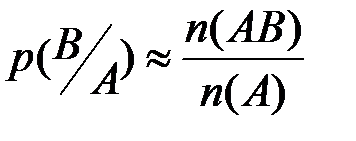Для условной вероятности 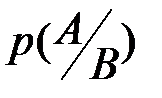подмножество 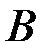является пространством элементарных событий с плотностью распределения вероятностей, равной 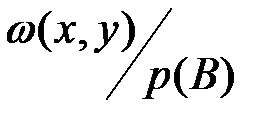, где 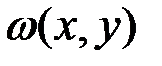- плотность распределения вероятностей в пространстве . Благодаря делению на 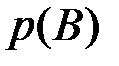подмножество 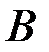становится полной группой событий. Устойчивость относительной частоты 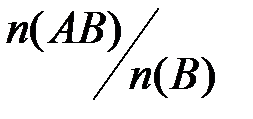появления события 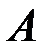при условии 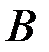является эмпирическим основанием для введения по аксиоме Колмогорова понятия условной вероятности 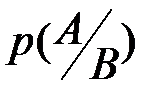. Поскольку 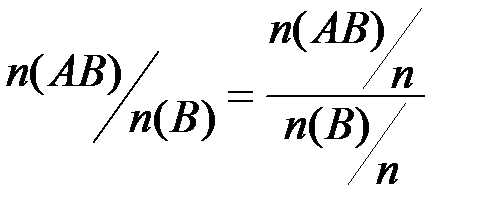, то, заменяя относительные частоты соответствующими вероятностями, получим 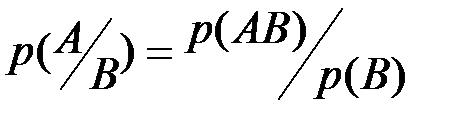, 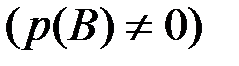и аналогично 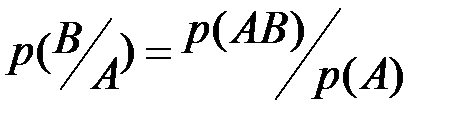( 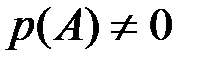). Отсюда очевидной становится формула умножения вероятностей: .

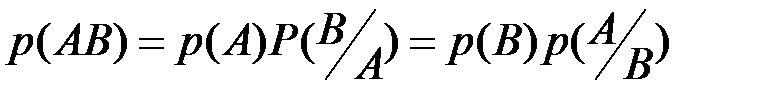Если имеет место равномерный закон распределения вероятностей в подмножестве 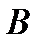, то значение вероятности 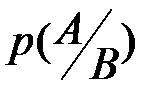можно вычислить как отношение площади пересечения событи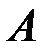й и 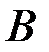к площади .

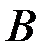Задача. Известно, что в результате 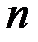испытаний событие 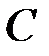появилось один раз. Какова вероятность того, что оно появилось при втором испытании? Вероятность появления события 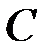при отдельном испытании равна .

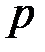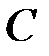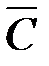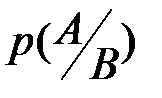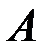Решение. Пространство элементарных событий для одного испытания состоит из событий и , которые в дальнейшем заменим соответственно на 1 и 0, а пространство элементарных событий для опыта состоит из 2ⁿ последовательностей. Необходимо вычислить условную вероятность , где ^_ событие, состоящее в том, что в результате опыта появится последовательность, содержащая единицу на втором месте. Это подмножество последовательностей, каждая из которых содержит 1 на втором месте. 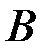^_ событие, состоящее в том, что последовательность будет содержать одну единицу. Пересечение событи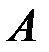й и 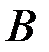состоит из единственной последовательности 010000…0. Все 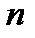последовательностей в 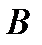равновероятны, поскольку вероятность каждой из них равна 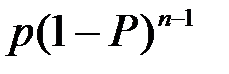, так как испытания независимы. Поэтому применим классический метод вычисления вероятностей, согласно которому .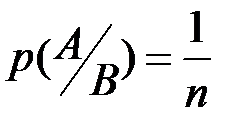