Эпюры распределенной нагрузки
Построение эпюр для балки.
Эпюры с точки зрения математики - это просто графики соответствующих функций, поэтому и правила построения эпюр ни чем не отличаются от общих правил построения графиков функций. Для этого достаточно иметь соответствующее функциональное или дифференциальное уравнение.
В частности именно для этого нас, начиная со средних классов школы, подгружали такими достаточно абстрактными математическими понятиями как переменные, функция, аргумент функции, график функции, производная и дифференциал функции.
При этом школьнику, особенно мечтающему стать писателем или водителем, труднее всего объяснить, зачем эти самые функции, графики и прочие абстракции ему нужны, если после экзаменов он больше никогда в жизни о них не вспомнит? Во всяком случае до тех пор, пока у него самого не появятся дети, которым снова нужно будет выучить эти понятия и термины.
Между тем с инженерами, физиками и представителями прочих точных наук дело обстоит иначе. Так например студенты строительных специальностей на втором году обучения с удивлением узнают, что у абстрактных функций и их графиков, а также производных и дифференциалов есть вполне конкретный смысл. А в чем этот смысл заключается, мы ниже и рассмотрим на примере балок.
Примечание: перед продолжением чтения данной статьи настоятельно рекомендую ознакомиться с основами теориисопротивления материалов.
Эпюры распределенной нагрузки
Это может показаться странным, но когда мы изображаем равномерно распределенную нагрузку, действующую по всей длине балки, например такую:
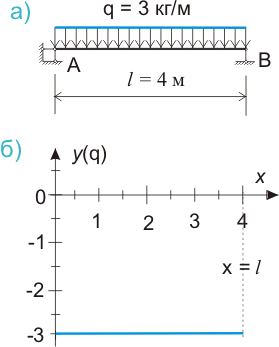
Рисунок 545.1. Равномерно распределенная нагрузка, а) общепринятое изображение, б) график функции - равномерно распределенной нагрузки
То это с одной стороны вроде бы просто нагрузка q = 3 кг/м, равномерно распределенная по всей длине балки (рис.545.1.а)), а с другой стороны - это график функции у, показывающий изменение значения функции в зависимости от изменения значения аргумента х (рис.545.1.б)). Соответственно функциональное уравнение в данном случае будет иметь вид:
у = - 3 = const (545.1)
или
q = - 3 = const (545.1.2)
А смысл этих достаточно простых уравнений в том, что значение нагрузки является постоянной величиной и не зависит от значения аргумента функции, в данном случае от положения рассматриваемого поперечного сечения.
Примечание: В данном случае знак "-" используется потому, что нагрузка направлена вниз.
Эпюра моментов строится с той стороны, где будет растянутая зона сечения. При этом момент, пытающийся вращать рассматриваемое сечение по часовой стрелке, считается положительным, а против часовой стрелки - отрицательным.
Примечание: это правило не является общепринятым. В некоторых справочниках и учебниках по теории сопротивления материалов положительный момент строится сверху от оси х, что в общем то логично, но при этом получается, что положительный момент там, где сжатая зона сечения. В других он строится с той стороны, где растянутая зона сечения, но при этом может показываться со знаком "-", если строится снизу от оси х. Но как я уже говорил выше, принципиального значения это не имеет, главное понимать общий смысл изгибающих моментов.
Если мы посмотрим на направление действия опорной реакции А и распределенной нагрузки q (рисунок 545.4), то увидим, что относительно любого из рассматриваемых сечений опорная реакция А пытается вращать это сечение по часовой стрелке, а распределенная нагрузка q - против. Это означает, что функциональное уравнение, описывающее изменение изгибающих моментов по длине балки, составлено у нас правильно.
При этом растянутой будет нижняя зона сечения балки по той причине, что балка прогнется вниз при таком действии нагрузки. Следовательно эпюру моментов в данном случае следует строить снизу от оси координат х.
Теперь у нас есть все данные для построения эпюры изгибающих моментов. Судя по уравнению (545.5.2) это будет квадратная парабола, а максимальное значение изгибающего момента будет посредине балки, так как нагрузка у нас симметричная, и составит М = 6·2 -3·22/2 = 6 кгм.
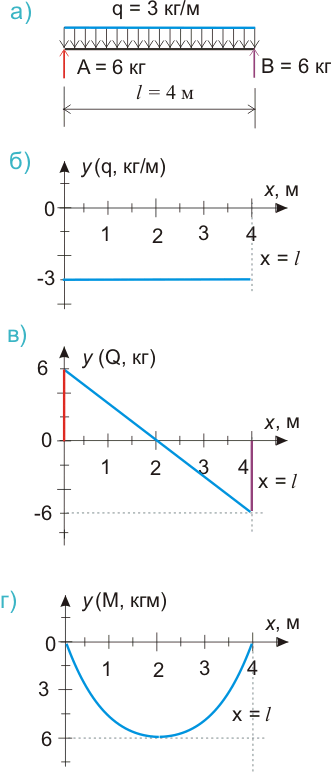
Рисунок 545.5.г) эпюра изгибающих моментов, как график функции у = 6х - 3х2/2
В общем случае, когда нагрузка несимметричная, как показано на рисунках 545.2.а) и б) или на балку действуют несколько распределенных нагрузок, то определить сечение в пролете балки, в котором действует максимальный изгибающий момент. можно, воспользовавшись следующим общим правилом:
Построение эпюр для балки.
Эпюры с точки зрения математики - это просто графики соответствующих функций, поэтому и правила построения эпюр ни чем не отличаются от общих правил построения графиков функций. Для этого достаточно иметь соответствующее функциональное или дифференциальное уравнение.
В частности именно для этого нас, начиная со средних классов школы, подгружали такими достаточно абстрактными математическими понятиями как переменные, функция, аргумент функции, график функции, производная и дифференциал функции.
При этом школьнику, особенно мечтающему стать писателем или водителем, труднее всего объяснить, зачем эти самые функции, графики и прочие абстракции ему нужны, если после экзаменов он больше никогда в жизни о них не вспомнит? Во всяком случае до тех пор, пока у него самого не появятся дети, которым снова нужно будет выучить эти понятия и термины.
Между тем с инженерами, физиками и представителями прочих точных наук дело обстоит иначе. Так например студенты строительных специальностей на втором году обучения с удивлением узнают, что у абстрактных функций и их графиков, а также производных и дифференциалов есть вполне конкретный смысл. А в чем этот смысл заключается, мы ниже и рассмотрим на примере балок.
Примечание: перед продолжением чтения данной статьи настоятельно рекомендую ознакомиться с основами теориисопротивления материалов.
Эпюры распределенной нагрузки
Это может показаться странным, но когда мы изображаем равномерно распределенную нагрузку, действующую по всей длине балки, например такую:

Рисунок 545.1. Равномерно распределенная нагрузка, а) общепринятое изображение, б) график функции - равномерно распределенной нагрузки
То это с одной стороны вроде бы просто нагрузка q = 3 кг/м, равномерно распределенная по всей длине балки (рис.545.1.а)), а с другой стороны - это график функции у, показывающий изменение значения функции в зависимости от изменения значения аргумента х (рис.545.1.б)). Соответственно функциональное уравнение в данном случае будет иметь вид:
у = - 3 = const (545.1)
или
q = - 3 = const (545.1.2)
А смысл этих достаточно простых уравнений в том, что значение нагрузки является постоянной величиной и не зависит от значения аргумента функции, в данном случае от положения рассматриваемого поперечного сечения.
Примечание: В данном случае знак "-" используется потому, что нагрузка направлена вниз.
