Линейные операции над векторами»
Блок «Матрицы»
1. Аnxn=(aij)
Сколько элементов расположено:
· Над главной диагональю:
· На главной диагонали:
· Под главной диагональю:
Ответ:
На главной диагонали: 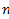
Под главной диагональю: : 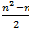
Над главной диагональю: : 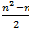
2. Запишите матрицы А3x3 элементы, которых aik определяются по форме:
1) aik=i+k;
2) aik=i∙k
3) aik=(i-k)2
4) aik=i2k+ik2
Совпадают ли элементы этих матриц расположенных симметрично относительно главной диагонали.
Ответ:
1) A= 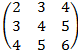
2) A= 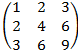
3) A= 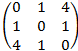
4) A= 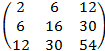
Да, совпадают.
3. Для каких матриц Аmxn существуют A+AT
Ответ:
Для квадратных матриц.
4. Найти матрицу Х удовлетворяющую условию 3A+2X=E, где Е – единичная матрица 3-его порядка и матрица А равна:
А= 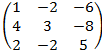
Ответ:
Х= 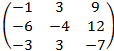
5. Известно, что A2x3∙Bmxn=С2x6. Найти m и n.
Ответ:
m=3; n=6
6. Даны матрицы A2x3, B3x1,C3x3. Существую ли произведения: АВ, ВA, AC, CA, ABC, CB, CBA, АСВ.
Ответ:
Существуют: АВ, AC,АСВ,СВ;
Не существуют: ВА, СА, АВС, СВА.
7. Найти сумму матриц А+В, разность А-В, произведение А∙В и В∙А, если существует:
· А= 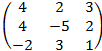 В=
В= 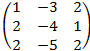
· А= 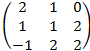 В=
В= 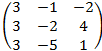
· А= 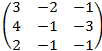 В=
В= 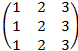
· А= 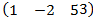 В=
В= 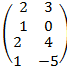
· А= 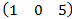 В=
В= 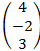
· А= 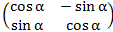 В=
В= 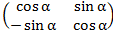
8. Найдите все матрицы перестановочные с матрицей:
А= 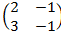
9. Вычислить степень приведённых ниже матриц:
· 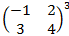
· 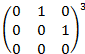
· 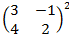
· 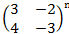
Ответ:
1. 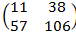
2. 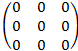
3. 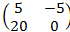
4. 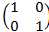 в четной степени, в нечетной степени- сама матрица.
в четной степени, в нечетной степени- сама матрица.
10. Используя равенства:
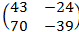 =
= 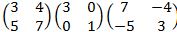 ;
;
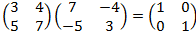 .
.
Вычислите
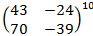
11. Докажите, что если матрицы А и В – перестановочные, то выполняется
(А+В)2=А2+2АВ+В2
(А+В)(А-В)=А2-В2
Верны ли эти равенства, если матрицы не являются перестановочными?
Ответ:
Если матрицы не перестановочные, равенство не выполняется.
12. Доказать, что если первая и вторая строки матрицы А равны, то первая и вторая строки матрицы АВ, так же равны.
13. Найдите f(A), если А= 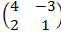
1. f(x) = x2-2x+5
2. f(x)=x2-5x+10
3. f(x)=(2x5-4x2+7)∙(x2-5x+10)+x+5
Ответ:
1. 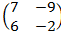
2. 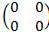
3. 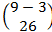
14. Вычислить определитель:
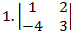 5.
5. 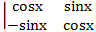
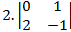 6.
6. 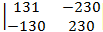
3. 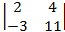 7.
7. 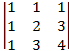
4. 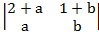 8.
8. 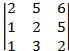
9. 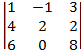
Найти x:
10. 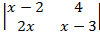 12.
12. 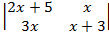
11. 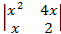
Доказать равенство:
13. 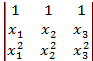 = (
= ( 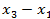 )(
)( 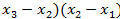
Ответ:
1. 11
2. -2
3. 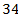
4. 2b-a
5. 1
6. 230
7. -1
8. -1
9. 0
10. X= 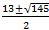
11. X= 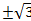
12. X= 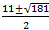
13. Доказано.
15. Вычислить определитель αA, если α= 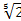 , а det А5x5=3
, а det А5x5=3
Ответ: 6
16. Дано: числа 185; 518; 851делятся на 37.
Докажите что определитель 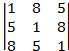 делится на 37 не вычисляя его.
делится на 37 не вычисляя его.
17. Вычислить определитель, раскладывая по элементам строки или столбцы, предварительно преобразовав их, используя свойства определителя.
1) 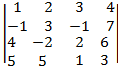
2) 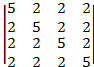
3) 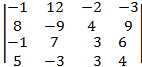
4) 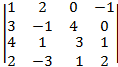
5) 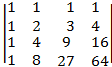
6) 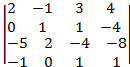
7) 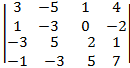
Ответ:
1. 900
2. 297
3. 150
4. -35
5. 12
6. 0
7. -110
18. Вычислить определитель, предварительно преобразовав его.
1) 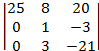
2) 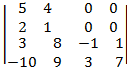
3) 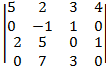
4) 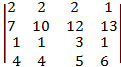
5) 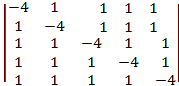
Ответ:
1. -300
2. 30
3. -30
4. 45
5. 0
19. Найти матрицы обратные данным. Полученный результат проверить, используя определение обратной матрицы
1. А= 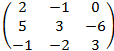
2. А= 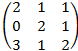
3. А= 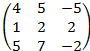
4. А= 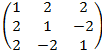
Ответ:
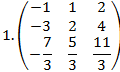
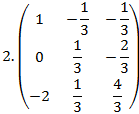
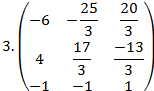
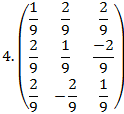
20. Найдите какой-либо базисный минор матрицы:
1) 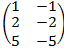
2) 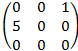
3) 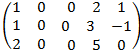
4) 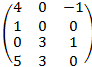
5) 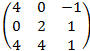
6) 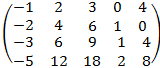
21. Проверить системы уравнений на совместность и в случае совместности данных систем уравнений решить их:
1. Методом Гаусса
2. Методом Крамера
3. Матричным методом
1. 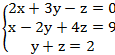
2. 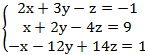
3. 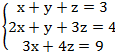
4. 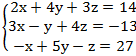
5. 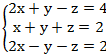
6. 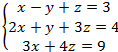
Ответ:
1. x=1 y=0 z=2
2. x= 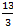 y= -
y= - 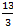 z= -
z= - 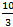
3. x=7 y=-1 z=-3
4. Решений нет
5. x= 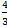 y=1 z= -
y=1 z= - 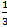
6. Ø
22. Решить системы уравнений Методом Гаусса;
1. 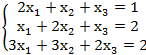
2. 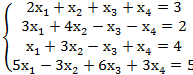
3. 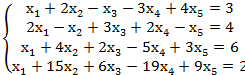
4. 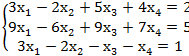
5. 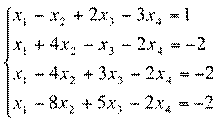
6. 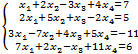
7. 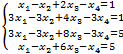
Ответ:
1. Нет решений
2. x1=1 ; х2=0 ;х3=-1 ;х4=2
3. решений нет
4. x2= 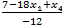 ; х1=R; x3=
; х1=R; x3= 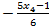 ; х4=R
; х4=R
5. x1=-8,x2=R,x3=2x2,x4=-3+x2
6. Нет решений
7. x1, x4 =R; x2=1+x1-x4; x3=1
23. Решить системы уравнений и найти нормированную фундаментальную систему решений:
1. 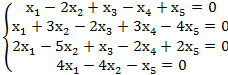
2. 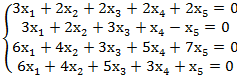
3. 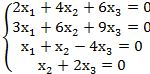
4. 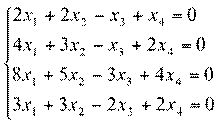
Ответ:
1. 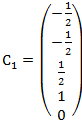
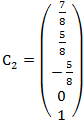
2. 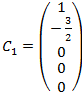
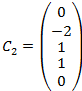
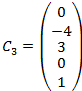
3.НФСР – не существует. Решение тривиальное.
4. тривиальное решение.
24. Решить систему при всевозможных значениях параметра λ
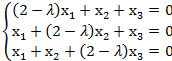
Ответ:Если λ≠1 и λ≠4, то Х1=Х2=Х3=0. Если λ=1, то Х1=-Х2-Х3, где Х2,Х3=R., если λ=4, то Х2=Х3; Х1=-3Х3, где Х3=R
Блок «Вектор.
Линейные операции над векторами»
Деление отрезка в заданном отношении
Задача 1
Даны точки: А (3;-1) и В (2;1).
Определить:
1)Координаты точки М симметричной точке А, относительно точки В. 2)Координаты точки N симметричной точке В, относительно точки А.
Ответ:N=(4;-3) M=(1;3)
Задача 2
Даны три вершины параллелограмма А (3;-5), В (5;-3), С (-1;3).
Определить четвертую вершину D противоположную В.
Ответ:(-3;-5)
Задача 3
Даны вершины треугольника: А (1;4), В (3;-9), С (-5;2). Определить длину его медианы, проведённой из вершины В.
Ответ:13
Задача 4
Отрезок, ограниченный точками: А (1;-3) и В (4;2), разделён на 3 равные части. Определить координаты точек деления.
Ответ:(2;-1) и (3;1)
Задача 5
Даны вершины треугольника: А (3;-5), В (-3;3), С (-1;-2). Определить длину биссектрисы его внутреннего угла при вершине А.
Ответ: 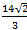
Полярная система координат
Задача 1
В полярной системе координат даны 2 вершины: А (3; 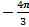 ) и В (5;
) и В (5; 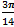 ) параллелограмма АВСD, точка пересечения диагоналей которого совпадает с полюсом. Определить две другие вершины этого параллелограмма.
) параллелограмма АВСD, точка пересечения диагоналей которого совпадает с полюсом. Определить две другие вершины этого параллелограмма.
Ответ:D (5; 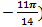 и С (1;
и С (1; 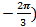
Задача 2
В полярной системе координат даны точки: А (8; 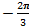 ) и В (6;
) и В (6;  ). Вычислить полярные координаты середины отрезка АВ.
). Вычислить полярные координаты середины отрезка АВ.
Ответ: С (1; 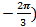
Задача 3
В полярной системе координат даны две противоположные вершины квадрата: Р (6; 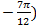 и Q (4;
и Q (4;  ). Определить площадь квадрата.
). Определить площадь квадрата.
Ответ: S=26+12 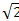
Задача 4
Полюс полярной системы координат совпадает с началом прямоугольной системой декартовых координат; а полярная ось совпадает с положительной полуосью абсцисс:
1) В полярной системе координат даны точки: 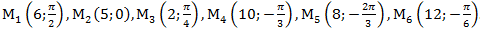
Определить, декартовы координаты этих точек.
2) В декартовой прямоугольной системе координат даны точки:
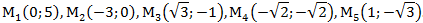
Определить полярные координаты этих точек.
Ответ:
1) 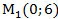
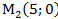
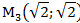
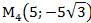
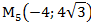
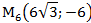
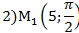
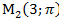
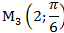
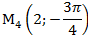
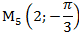
Задача 5
Установить какие линии определяются в полярных координатах следующими уравнениями:
1) 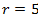 , 2)
, 2) 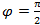 , 3)
, 3) 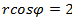 , 4)
, 4) 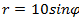
Ответ:
1) Окружность, 2) Луч, 3) Прямая,
4) Окружность R=5 с центром в точке (0;5).
Вектор. Координаты вектора.
Задача 1
Определить начало вектора  (2;-3;-1), если его конец совпадает с точкой
(2;-3;-1), если его конец совпадает с точкой
(1;-1;2)
Ответ: (-1;2;3)
Задача 2
Дан модуль вектора 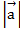 =2 и углы, которые вектор образует с координатными осями ОХ:
=2 и углы, которые вектор образует с координатными осями ОХ: 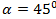 , ОУ:
, ОУ: 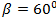 , OZ:
, OZ: 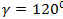 .
.
Вычислить проекции 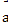 на координатные оси.
на координатные оси.
Ответ: ( 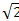 ;1;-1)
;1;-1)
Задача 3
Вычислить направляющие 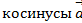 с координатами (12;-15;-16).
с координатами (12;-15;-16).
Ответ: ( 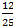 ;
; 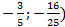
Задача 4
Может ли вектор составлять с координатными осями следующие углы:
1) 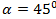 ,
, 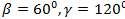
2) 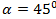 ,
, 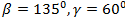
3) 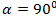 ,
, 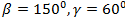
Ответ: Могут 1 и 3.
Задача 5
Вектор составляет с осями ОХ и OZ углы: 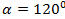 ,
, 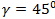 . Какой угол он составляет с осью ОУ?
. Какой угол он составляет с осью ОУ?
Ответ: 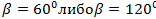
Задача 6
Вектор  составляет с координатными осями ОХ и ОУ углы:
составляет с координатными осями ОХ и ОУ углы:
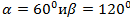 .
.
Вычислить его координаты при условии, что модуль вектора 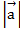 =2.
=2.
Ответ: (1;-1; 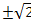 )
)
Задача 1
Дано:
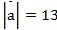
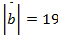
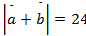
Найти: 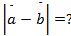
Ответ: 22
Задача 2
Дано:
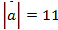
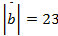
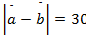
Найти: 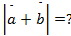
Ответ: 20
Задача 3
Даны 2 вектора  (3;-2;6) и
(3;-2;6) и 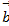 (-2;1;0).
(-2;1;0).
Определить проекцию на координатную оси и модули векторов 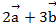 и
и 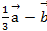
Ответ: 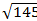 ;
; 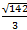
Задача 4
Проверить коллинеарность векторов  (2;-1;3) и
(2;-1;3) и 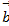 (-6;3;-9). Установить какой из них длиннее и во сколько раз.
(-6;3;-9). Установить какой из них длиннее и во сколько раз.
Как они направлены: в одну или противоположные стороны?
Ответ:
Вектор 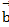 длиннее вектора
длиннее вектора  в 3 раза.
в 3 раза.
Задача 5
Определить при каких значениях 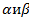 векторы:
векторы:
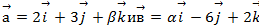 коллинеарны.
коллинеарны.
Ответ: 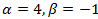
Задача 6
Проверить, что точки А (3;-1;2), В (1;2;-1), С (-1;1;-3), D (3;-5;3) служат вершинами трапеции.
Задача 7
Даны 3 вектора 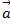 (3;-1),
(3;-1), 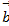 (1;-2),
(1;-2), 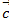 (-1; 7).
(-1; 7).
Определить разложение вектора 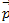 =
= 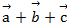 по базису
по базису 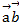 .
.
Ответ: p= 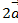 -3
-3 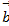
Задача 8
Даны 4 вектора  (2;1;0),
(2;1;0), 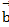 (1;-1;2),
(1;-1;2), 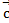 (2;2;-1),
(2;2;-1), 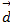 (3;7;-7).
(3;7;-7).
Определить разложения каждого из этих 4-х векторов принимая в качестве базиса 3 остальных.
Ответ:
· 2 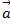 -3
-3 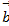 -
- 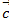
· -2 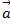 +3
+3 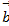 +
+ 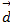
· 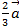 +
+ 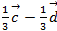
· 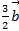 +
+ 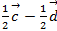
Задача 1
Векторы 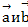 взаимно перпендикулярны,
взаимно перпендикулярны, 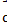 образует с ними угол
образует с ними угол  .
.
Зная, что 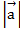 =3,
=3, 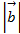 =5,
=5, 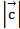 =8 вычислить:
=8 вычислить:
1)( 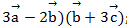
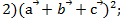
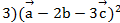
Ответ: 1)-62, 2)162, 3) -34
Задача 2
Векторы 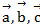 попарно образуют друг с другом углы, каждый их которых равен
попарно образуют друг с другом углы, каждый их которых равен 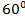 . Зная, что
. Зная, что 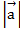 =4,
=4, 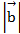 =2,
=2, 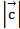 =6, определить модуль
=6, определить модуль 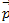 =
= 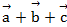
Ответ: 10.
Задача 3
Векторы 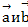 образуют угол, равный
образуют угол, равный  . Зная, что
. Зная, что 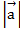 =
= 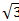 ,
, 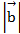 =1, вычислить угол между векторами:
=1, вычислить угол между векторами:
р= 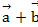 ;
;
q= 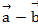
Ответ: 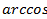
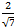 .
.
Задача 4
Даны векторы  (4;-2;-4),
(4;-2;-4), 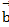 (6;-3;2).
(6;-3;2).
Вычислить 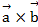 ; (
; ( 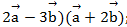 (
( 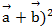 .
.
Ответ: 22;-200, 129
Задача 5
Даны силы 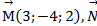 (2;3;-5),
(2;3;-5), 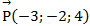 Вычислить, какую работу производит равнодействующая этих сил, когда её точка приложения двигаясь прямолинейно перемещалась из положения
Вычислить, какую работу производит равнодействующая этих сил, когда её точка приложения двигаясь прямолинейно перемещалась из положения 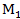 (5;3;-7) в положение
(5;3;-7) в положение 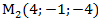 .
.
Ответ: 13.
Задача 6
Даны вершины треугольника: 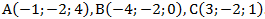 Определить его внутренний угол при вершине В.
Определить его внутренний угол при вершине В.
Ответ: 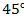
Задача 7
Найти вектор 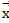 коллинеарный вектору
коллинеарный вектору 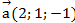 и удовлетворяющий условию
и удовлетворяющий условию 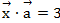
Ответ:(1;1/2;-1/2)
Задача 8
Даны векторы 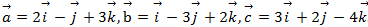
Найти вектор 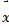 удовлетворяющий условию:
удовлетворяющий условию: 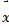 ∙
∙ 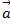 =-5,
=-5, 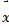 ∙
∙ 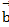 =-11,
=-11, 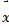 ∙
∙ 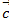 =20.
=20.
Ответ: (2;3;-2).
Задача 9
Вычислить проекцию вектора  с координатами (5;2;5) на ось вектора
с координатами (5;2;5) на ось вектора 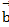 с координатами (2;-1;2)
с координатами (2;-1;2)
Ответ: 6.
Задача 10
Даны вектора 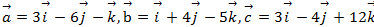
Вычислить проекцию 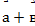 на вектор
на вектор 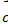 .
.
Ответ: -4.
Задача 11
Даны точки 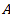 (-2;3;-4),
(-2;3;-4), 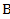 (3;2;5),
(3;2;5), 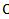 (1;-1;2),
(1;-1;2), 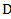 (3;2;-4).
(3;2;-4).
Вычислить проекцию вектора 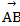 на вектор
на вектор 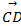 .
.
Ответ: 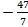 .
.
Задача 12
Вектор 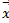 перпендикулярен вектору
перпендикулярен вектору 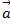 = 3
= 3 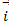 +2
+2 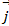 +2
+2 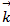 и перпендикулярен вектору
и перпендикулярен вектору 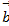 = 18
= 18 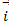 -22
-22 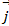 -5
-5 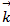 , модуль х = 14. Вектор
, модуль х = 14. Вектор 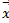 образует с осью Oу тупой угол. Чему равен вектор
образует с осью Oу тупой угол. Чему равен вектор 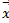 .
.
Ответ: (-4;-6;12)
Задача 1
Даны векторы 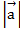 = 10,
= 10, 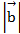 = 2,
= 2, 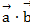 = 12.
= 12.
Найти 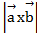 .
.
Ответ: 16
Задача 2
Даны векторы 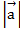 = 3,
= 3, 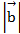 = 26,
= 26, 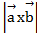 = 72.
= 72.
Найти 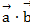 .
.
Ответ: 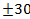
Задача 3
Векторы  и
и  образуют угол
образуют угол 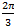 .
.
Зная, что 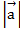 = 1,
= 1, 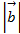 = 2, вычислить:
= 2, вычислить:
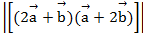 и
и 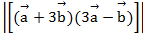 .
.
Ответ: 3 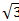 и 10
и 10 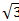
Задача 4
Даны вектор  (3;-1;-2) и
(3;-1;-2) и 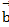 (1;2;-1).
(1;2;-1).
Найти 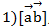
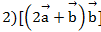 ,
, 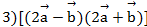 .
.
Ответ: 1) (5;1;7), 2) (10;2;14), 3) (20;4;28).
Задача 5
Даны точки А (2;-1;2), В (1;2;-1), С (3;2;1).
Найти координаты векторных произведений 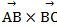 и (
и ( 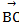 -2
-2 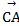 )
) 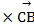 .
.
Ответ: (6;-4;-6) (-12;8;12).
Задача 6
Даны точки А (1;2;0), В (3;0;-3), С (5;2;6).
Вычислить площадь треугольника АВС.
Ответ: 14
Задача 7
Даны вершины треугольника точки А (1;-1;2), В (5;-6;2), С (1;3;-1). Вычислить длину его высоты, опущенной из вершины В на АС.
Ответ: 5
Задача 8
Вычислить sin угла, образованного векторами  (2;-2;1),
(2;-2;1), 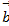 (2;3;6).
(2;3;6).
Ответ: 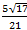 .
.
Задача 1
Вектор 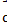 перпендикулярен векторам
перпендикулярен векторам  и
и  , угол между которыми
, угол между которыми 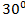 . Зная, что
. Зная, что 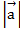 =6,
=6, 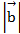 =3,
=3, 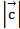 =3, вычислить смешанное произведение
=3, вычислить смешанное произведение 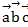
Ответ: 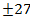
Задача 2
Вектора 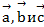 , образующие правую тройку взаимно перпендикулярны. Зная, что
, образующие правую тройку взаимно перпендикулярны. Зная, что 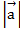 =4,
=4, 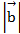 =2,
=2, 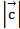 =3, вычислить смешанное произведение векторов
=3, вычислить смешанное произведение векторов 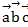
Ответ:24
Задача 3
Установить компланарны ли векторы 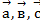 , если
, если
1)  (2;3;-1),
(2;3;-1), 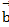 (1;-1;3),
(1;-1;3), 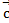 (1;9;-11)
(1;9;-11)
2)  (3;-2;1),
(3;-2;1), 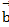 (2;1;2),
(2;1;2), 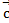 (3;-1;-2)
(3;-1;-2)
3)  (2;-1;2),
(2;-1;2), 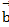 (1;2;-3),
(1;2;-3), 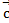 (3;-4;7)
(3;-4;7)
Ответ:
1) Вектора компланарны;
2) Вектора не компланарны;
3) Вектора компланарны.
Задача 4
Доказать, что точки А (1;2;-1), В (0;1;5), С (-1;2;1), D (2;1;3) лежат в одной плоскости.
Задача 5
Вычислить объём тетраэдра, вершины которого находятся в точках:
А (2;-1;1), В (5;5;4), С (3;2;-1), D (4;1;3).
Ответ: 3.
Задача 6
Даны вершины тетраэдра А (2;3;1), В (4;1;-2), С (6;3;7), D (-5;-4;8).
Найти длину его высоты, опущенной из вершины D.
Ответ: 11
Задача 7
Объём тетраэдра равен 5. Три его вершины находятся в точках А (2;1;-1), В (3;0;1), С (2;-1;3).
Найти координаты четвёртой вершины D, если известно, что она лежит на оси OY.
Ответ: 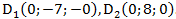
Задача 1
Даны уравнения двух сторон параллелограмма : 8х+3у+1=0 и 2х+у-1=0. Уравнение одной из диагоналей 3х+2у+3=0 . Определить координаты вершин параллелограмма.
Ответ:A(1, -3), B(-2, 5), C(5, -9), E(8, -17).
Задача 2
Найти точку Q симметричную точке D (-5; 13) относительно прямой
2х-3у-3=0
Ответ: (11; -11)
Задача 3
Составить уравнения сторон треугольника, зная одну его вершину С (4; -1), а также уравнение высоты: 2х-3у+12=0 и медианы 2х+3у=0, проведённой их первой вершины.
Ответ:
1. уравнение АВ имеет вид 9х+11у+5=0
2. уравнение АС имеет вид 3х+7у-5=0
3. уравнение ВС имеет вид 3х+2у-10=0
Задача 4
Определить при каких значениях m и n, две прямые:
mх+8у+n=0
2x+my-1=0
1) Параллельны
2) Совпадают
3) Перпендикулярны
Ответ:
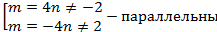
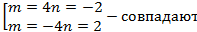
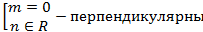
Задача 5
Определить угол, образованный двумя прямыми:
1) 3х-у+5=0, 2х+у-7=0
2)х 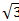 +у
+у 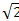 -2=0, х
-2=0, х 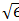 -3у+3=0
-3у+3=0
Ответ:
· 30о
· 45o
Уравнение плоскости
Задача 1
Составить уравнение плоскости, которая проходит через начало координат перпендикулярно вектору 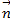 (5;0-3)
(5;0-3)
Ответ: 5х-3z=0
Задача 2
Составить уравнение плоскости, проходящей через точку 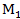 (3;4;-5) параллельно векторам:
(3;4;-5) параллельно векторам: 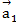 (3;1;-1);
(3;1;-1); 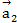 (1;-2;1)
(1;-2;1)
Ответ: x+4y+7z+16=0
Задача 3
Установить какие из следующих пар уравнений прямых параллельны плоскости:
1) 2x-3y+5z-7=0; 2x-3y+5z+3=0
2) 4x+2y-4z+5=0; 2x+y+2z-1=0
3) x-3z+2=0; 2x-z-7=0
Ответ:1 – параллельны, 2 – не параллельны, 3 –не параллельны
Задача 4
Определить при каком значении L следующие пары уравнений будут задавать перпендикулярные плоскости:
1) 3х-5у+Lz-3=0; x+3y+2z+5=0
2) 5x+y-3z-3=0; 2x+Ly-3z+1=0
Ответ: 1) L=6; 2) L=-19
Задача 5
Составить уравнение плоскости, которая проходит через 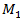 (3;-2;-7) параллельно плоскости
(3;-2;-7) параллельно плоскости
2x-3z+5=0.
Ответ: 2x-3z-27=0
Задача 6
Составить уравнение плоскости, которая проходит через 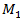 (2;-1;1) перпендикулярно к двум плоскостям:
(2;-1;1) перпендикулярно к двум плоскостям:
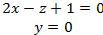
Ответ: x+2z-4=0
Задача 7
Плоскость проходит, через 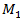 (6;-10;1) и отсекает на оси абсцисс отрезок
(6;-10;1) и отсекает на оси абсцисс отрезок
а=-3, на оси опликат с=2. Составить для плоскости уравнение в отрезках.
Ответ: 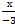 +
+ 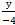 +
+ 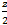 =1
=1
Задача 8
Найти расстояние от Р(-1;1;-2) до плоскости, проходящей через 3 точки:
1) 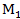 (1;-1;1)
(1;-1;1)
2) 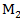 (-2;1;3)
(-2;1;3)
3) 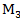 (4;-5;-2)
(4;-5;-2)
Ответ: 4.
Задача 9
Вычислить объём пирамиды, ограниченной плоскостью 2x-3y+6z-12=0 и координатными плоскастями.
Ответ: 8.
Задача 10
Определить лежит ли точка Q(2;-1;1) и начало координат по одну или по разные стороны относительно каждой из следующих плоскостей:
1) 5x-3y+z=0
2) 2x+7y+3z=0
3) x+5y+12z=0
Ответ:1)по одну сторону
2)по разные стороны
3)по разный стороны
Задача 11
В каждом из следующих случаев вычислить расстояние между параллельными плоскостями:
1) x-2y-2z-12=0, x-2y-2z-6=0
2) 2x-3y+6z-14=0, 4x-6y+12z+21=0
3) 2x-y+2z+9=0, 4x-2y+4z-21=0
Ответ: 1) 2
2) 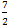
Задача 12
Доказать, что плоскость 3x-4y-2z+5=0 пересекает отрезок, ограниченный точками 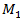 (3;-2;1) и
(3;-2;1) и 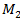 (-2;5;2)
(-2;5;2)
Задача 13
Составить уравнение плоскостей, параллельных плоскости 2x-2y-z=0 и относящихся от неё на расстояние d=5.
Ответ: 2x-2y-z+12 или -18=0
Задача 1
Составить канонические уравнения прямой, проходящей через точку
