Основные свойства определённого интеграла
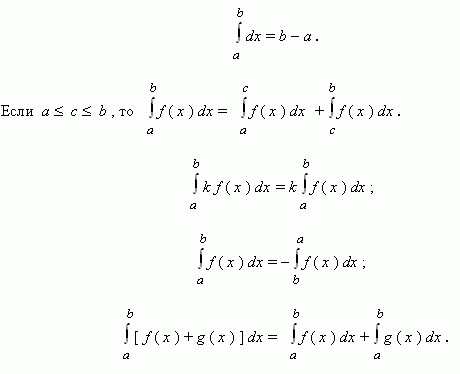 Пространство элементарных событий. Событие: невозможное, достоверное, случайное. Действия над событиями. Под событием в теории вероятностей понимают любой факт, который может произойти или не произойти в результате опыта со случайным исходом. Самый простой результат такого опыта (например, появление "орла" или "решки" при бросании монеты, попадание в цель при стрельбе, появление туза при вынимании карты из колоды, случайное выпадение числа при бросании игральной кости и т.д.) называется элементарным событием. Множество всех элементарных событий Е называется пространством элементарных событий. Так, при бросании игральной кости это пространство состоит из шести элементарных событий, а при вынимании карты из колоды – из 52. Событие может состоять из одного или нескольких элементарных событий, например, появление двух тузов подряд при вынимании карты из колоды, или выпадение одного и того же числа при трёхкратном бросании игральной кости. Тогда можно определить событие как произвольное подмножество пространства элементарных событий. Достоверным событием называется всё пространство элементарных событий. Таким образом, достоверное событие – это событие, которое обязательно должно произойти в результате данного опыта. При бросании игральной кости таким событием является её падение на одну из граней. Невозможным событием ( Пространство элементарных событий. Событие: невозможное, достоверное, случайное. Действия над событиями. Под событием в теории вероятностей понимают любой факт, который может произойти или не произойти в результате опыта со случайным исходом. Самый простой результат такого опыта (например, появление "орла" или "решки" при бросании монеты, попадание в цель при стрельбе, появление туза при вынимании карты из колоды, случайное выпадение числа при бросании игральной кости и т.д.) называется элементарным событием. Множество всех элементарных событий Е называется пространством элементарных событий. Так, при бросании игральной кости это пространство состоит из шести элементарных событий, а при вынимании карты из колоды – из 52. Событие может состоять из одного или нескольких элементарных событий, например, появление двух тузов подряд при вынимании карты из колоды, или выпадение одного и того же числа при трёхкратном бросании игральной кости. Тогда можно определить событие как произвольное подмножество пространства элементарных событий. Достоверным событием называется всё пространство элементарных событий. Таким образом, достоверное событие – это событие, которое обязательно должно произойти в результате данного опыта. При бросании игральной кости таким событием является её падение на одну из граней. Невозможным событием ( 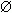 ) называется пустое подмножество пространства элементарных событий. То есть, невозможное событие не может произойти в результате данного опыта. Так, при бросании игральной кости невозможным событием является её падение на ребро. События А и В называются тождественными ( А = В ),если событие А происходит тогда и только тогда, когда происходит событие В . Событие А' называется противоположным событию А , если не произошло событие А. Так, промах и попадание при стрельбе – противоположные события. События А и В называются несовместными ( А ) называется пустое подмножество пространства элементарных событий. То есть, невозможное событие не может произойти в результате данного опыта. Так, при бросании игральной кости невозможным событием является её падение на ребро. События А и В называются тождественными ( А = В ),если событие А происходит тогда и только тогда, когда происходит событие В . Событие А' называется противоположным событию А , если не произошло событие А. Так, промах и попадание при стрельбе – противоположные события. События А и В называются несовместными ( А  В = В = 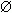 ) ,если их одновременное появление невозможно. Например, выпадение и "решки", и "орла" при бросании монеты. Если при проведении опыта могут произойти несколько событий и каждое из них по объективным условиям не является более возможным, чем другое, то такие события называются равновозможными. Примеры равновозможных событий: появление двойки, туза и валета при вынимании карты из колоды, выпадение любого из чисел от 1 до 6 при бросании игральной кости и т.п. Классическое определение вероятности. Пусть пространство элементарных событий Е состоит из N равновозможных элементарных событий, среди которых имеется n событий, благоприятствующих событию А , тогда число Р ( А ) = n / N называется вероятностью события А . Основные свойства вероятности. Пусть задано пространство элементарных событий Е , а вероятности Р определены на событиях из Е . Тогда: ) ,если их одновременное появление невозможно. Например, выпадение и "решки", и "орла" при бросании монеты. Если при проведении опыта могут произойти несколько событий и каждое из них по объективным условиям не является более возможным, чем другое, то такие события называются равновозможными. Примеры равновозможных событий: появление двойки, туза и валета при вынимании карты из колоды, выпадение любого из чисел от 1 до 6 при бросании игральной кости и т.п. Классическое определение вероятности. Пусть пространство элементарных событий Е состоит из N равновозможных элементарных событий, среди которых имеется n событий, благоприятствующих событию А , тогда число Р ( А ) = n / N называется вероятностью события А . Основные свойства вероятности. Пусть задано пространство элементарных событий Е , а вероятности Р определены на событиях из Е . Тогда: 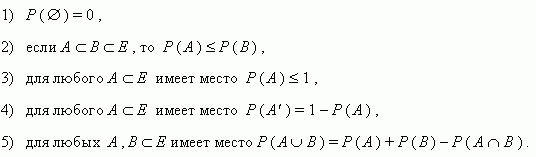 |
Условная вероятность. Независимость событий
Вероятность появления события А при условии, что событие В произошло, называется условной вероятностью события А и вычисляется по формуле:
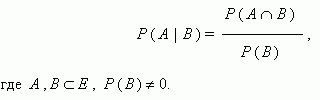
События А , В  Е называются независимыми, если Р ( А
Е называются независимыми, если Р ( А  В ) = Р ( А ) · Р ( В ) .
В ) = Р ( А ) · Р ( В ) .
В противном случае события А и В называются зависимыми.
