Физический смысл производной.

Если функция y = f(x) и ее аргумент x являются физическими величинами, то производная 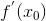– это скорость изменения переменной y относительно переменной x в точке 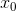. Например, если S = S(t) – расстояние, проходимое точкой за время t, то ее производная 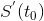– скорость в момент времени 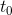. Если q = q(t) – количество электричества, протекающее через поперечное сечение проводника в момент времени t, то 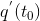– скорость изменения количества электричества в момент времени 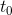, т.е. сила тока в момент времени .

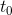Геометрический смысл производной.

Пусть 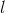– некоторая кривая, 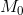– точка на кривой .

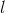Любая прямая, пересекающая 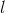не менее чем в двух точках называется секущей.

Касательной к кривой 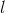в точке 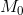называется предельное положение секущей 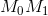, если точка 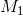стремится к 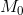, двигаясь по кривой.

Из определения очевидно, что если касательная к кривой в точке 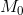существует, то она единственная.

Рассмотрим кривую y = f(x) (т.е. график функции y = f(x)). Пусть в точке 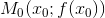он имеет невертикальную касательную 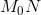. Ее уравнение: 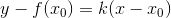(уравнение прямой, проходящей через точку 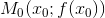и имеющую угловой коэффициент k).

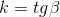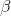По определению углового коэффициента , где – угол наклона прямо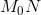й к оси .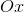

Пусть 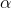– угол наклона секуще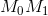й к оси 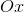, где 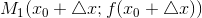. Так как 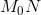– касательная, то при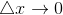

⇒ ⇒ .

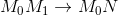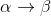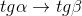Следовательно,

Таким образом, получили, что 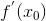– это угловой коэффициент касательной к графику функции y = f(x) в точке 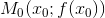(геометрический смысл производной функции в точке).Поэтому уравнение касательной к кривой y = f(x) в точке 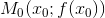можно записать в виде

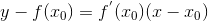
Правила дифференцирования

1) Производная константы равна нулю, т.е 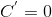, где C – константа.

2) Производная суммы (разности) дифференцируемых функций равна сумме (разности) производных этих функций, т.е . .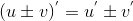

3) Производная произведения дифференцируемых функций находится по правилу: .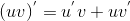

4) Константу можно выносить за знак производной : 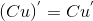, где 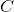- константа.

5) Производная дроби находится по правилу: .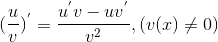

Правило дифференцирования сложной функции.

6) Если функция 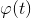имеет производную в точке 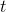, а функция 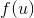имеет производную в точке 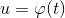, то сложная функция 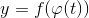имеет производную в точке 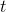, причем .

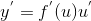Первообразная. Неопределённый интеграл

Первообразная.Непрерывная функция F ( x ) называется первообразной для функции f ( x ) на промежутке X , если для каждого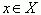

F’ ( x ) = f ( x ).

П р и м е р . Функция F ( x ) = x ³ является первообразной для функции

f ( x ) = 3x ² на интервале ( - 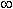, + 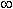) , так как

F’ ( x ) = ( x ³)’ = 3x ² = f ( x ) для всех x 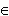( - 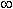, + 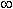) . Легко проверить, что функция x ³ + 13 имеет ту же производную 3x ², поэтому x ³ + 13 также является первообразной для функции 3x ² для всех x 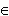( - 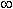, + 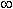) . Ясно, что вместо 13 можно взять любую постоянную.

Таким образом, задача нахождения первообразной имеет бесчисленное множество решений. Этот факт нашёл отражение в определении неопределённого интеграла.

Неопределённый интеграл функции f ( x ) на промежутке X есть множество всех её первообразных. Это записывается в виде:

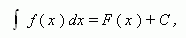
где C – любая постоянная, называемая постоянной интегрирования.