Понятие функции. Отображение множеств
Элементы теории множеств
Понятие множества
В математике встречаются самые разнообразные множества. Можно говорить о множестве граней многогранника, точек на прямой, множестве натуральных чисел и т.д. Понятие множества относится к числу первоначальных понятий, которые не определяются через другие, более простые. Вместо слова ''множество'' иногда говорят ''совокупность'', ''собрание'' предметов и т.д. Предметы, составляющие данное множество, называются элементами данного множества.
Теория множеств посвящена в основном изучению именно бесконечных множеств. Теория конечных множеств называется иногда комбинаторикой.
Но простейшие свойства множеств, те, о которых мы только и будем здесь говорить, в большинстве случаев в равной мере относятся как к конечным, так и к бесконечным множествам.
Заметим, что в математике допускается к рассмотрению множество, не содержащее элементов – пустое множество. Запись а Î Х означает, что а есть элемент множества Х.
Определение. Множество В называется подмножеством множества А, если каждый элемент множества В является в то же время элементом множества А.
Каждый отдельный элемент множества А образует подмножество, состоящего из этого одного элемента. Кроме того, пустое множество является подмножеством всякого множества.
Подмножество множества А называется несобственным, если оно совпадает с множеством А.
Если множество В есть подмножество множества А, то говорим, что В содержится в А и обозначаем В Í А. Подмножество В множества А называется собственным подмножеством, если В не пусто и не совпадает с А (т.е. имеется элемент множества А, не содержащийся в В).
Операции над множествами
Пусть А и В – произвольные множества.
Определение. Объединением двух множеств А и В называется множество С = АÈВ, состоящее из всех элементов, принадлежащих хотя бы одному из множеств А и В. (см. рис. 1).
Аналогично определяется объединение любого (конечного или бесконечного) числа множеств: если Аi – произвольные множества, то их объединение 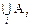 есть совокупность элементов, каждый из которых принадлежит хотя бы одному из множеств Аi.
есть совокупность элементов, каждый из которых принадлежит хотя бы одному из множеств Аi.
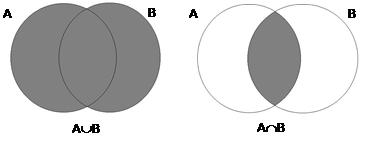 |
Рис.1 Рис.2
Определение. Пересечением множеств А и В называется множество С = АÇВ, состоящее из всех элементов, принадлежащих как А, так и В (см. рис. 2). Пересечением любого (конечного или бесконечного) числа множеств Аi называется множество  элементов, принадлежащих каждому из множеств Аi.
элементов, принадлежащих каждому из множеств Аi.
Операции объединения и пересечения множеств по определению коммутативны и ассоциативны, т.е.
АÈВ = В È А, (А ÈВ) ÈС = А È (В È С),
А Ç В = В Ç А, (А Ç В) Ç С = А Ç (В Ç С).
Кроме того, они взаимно дистрибутивны:
(А È В) Ç С = (А Ç С) È (В Ç С), (1)
(А Ç В) È С = (А È С) Ç (В È С). (2)
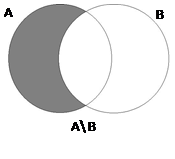
Определение. Разностью множеств А и В называется множество тех элементов из А, которые не содержатся в В (рис. 3).
 |
Непрерывность функции
1.1. Непрерывность функции в точке Определение. Функция у = f(x), определённая на интервале ]a, b[, называется непрерывной в точке х0 Î ]a, b[, если 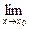 f(х) = f(х0) (то есть предел функции равен её значению при предельном значении аргумента). Так как равенство в определении равносильно следующему f(х) = f(х0) (то есть предел функции равен её значению при предельном значении аргумента). Так как равенство в определении равносильно следующему 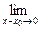 (f(х) – f(х0)) = 0, то функция непрерывна в точке, если бесконечно малому приращению аргумента в этой точке соответствует бесконечно малое приращение функции. Теорема 1.1.1. Если функции f(x) и j(х) непрерывны в точке х (f(х) – f(х0)) = 0, то функция непрерывна в точке, если бесконечно малому приращению аргумента в этой точке соответствует бесконечно малое приращение функции. Теорема 1.1.1. Если функции f(x) и j(х) непрерывны в точке х 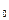 , то также непрерывны в этой точке их сумма f(x) + j(х), разность f(x) – j(х), произведение f(x)×j(х), а также частное , то также непрерывны в этой точке их сумма f(x) + j(х), разность f(x) – j(х), произведение f(x)×j(х), а также частное 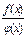 при условии, что j(х) ¹ 0. Следствие 1. Целая рациональная функция Рn(х) = a0 + a1x + a2x2 + … + anxn непрерывна при всех х. Следствие 2. Дробно рациональная функция при условии, что j(х) ¹ 0. Следствие 1. Целая рациональная функция Рn(х) = a0 + a1x + a2x2 + … + anxn непрерывна при всех х. Следствие 2. Дробно рациональная функция 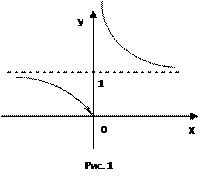 R(x) = R(x) = 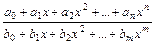 непрерывна при всех х, для которых знаменатель не обращается в нуль. Теорема 1.1.2. Если функция j(х) непрерывна в точке х0, а функция f(у) непрерывна в точке у0 = j(х0), то сложная функция F(x) = f(j(х)) непрерывна в точке х0. 1.2 Точки разрыва функции Рассмотрим функцию у = f(x), определённую на интервале ]a, b[, кроме, быть может, точки х0 Î ]a, b[. Определение. Точка х0 называется точкой разрыва данной функции, если в ней функция определена, но не является непрерывной, или не определена в этой точке. Если х0 – точка разрыва функции f(x) и существуют конечные пределы f(х0 – 0) = непрерывна при всех х, для которых знаменатель не обращается в нуль. Теорема 1.1.2. Если функция j(х) непрерывна в точке х0, а функция f(у) непрерывна в точке у0 = j(х0), то сложная функция F(x) = f(j(х)) непрерывна в точке х0. 1.2 Точки разрыва функции Рассмотрим функцию у = f(x), определённую на интервале ]a, b[, кроме, быть может, точки х0 Î ]a, b[. Определение. Точка х0 называется точкой разрыва данной функции, если в ней функция определена, но не является непрерывной, или не определена в этой точке. Если х0 – точка разрыва функции f(x) и существуют конечные пределы f(х0 – 0) = 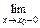 f(х), f(х0 + 0) = f(х), f(х0 + 0) = 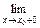 f(х), то она называется точкой разрыва первого рода. Величина f(х0 + 0) – f(х0 – 0) называется скачком функции f(x) в точке х0. Пусть функция у = f(x) имеет разрыв в точке х0 и f(х0 + 0) = f(х0 – 0), тогда х0 называется точкой устранимого разрыва. Это название оправдано тем, что если доопределить такую функцию (если она не была определена в точке х0), положив f(х0) = f(х), то она называется точкой разрыва первого рода. Величина f(х0 + 0) – f(х0 – 0) называется скачком функции f(x) в точке х0. Пусть функция у = f(x) имеет разрыв в точке х0 и f(х0 + 0) = f(х0 – 0), тогда х0 называется точкой устранимого разрыва. Это название оправдано тем, что если доопределить такую функцию (если она не была определена в точке х0), положив f(х0) = 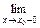 f(х) = f(х) = 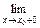 f(х), то получится функция, непрерывная в точке х0. Например, для функции f(x) = f(х), то получится функция, непрерывная в точке х0. Например, для функции f(x) = 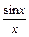 точка х0 = 0 является точкой устранимого разрыва. Если х0 – точка разрыва и, по крайней мере, один из пределов f(х0 + 0), f(х0 – 0) является бесконечным или не существует, то х0 называется точкой разрыва второго рода. Например, 1) точка х0 = 0 – точка разрыва второго рода для функции f(x) = точка х0 = 0 является точкой устранимого разрыва. Если х0 – точка разрыва и, по крайней мере, один из пределов f(х0 + 0), f(х0 – 0) является бесконечным или не существует, то х0 называется точкой разрыва второго рода. Например, 1) точка х0 = 0 – точка разрыва второго рода для функции f(x) = 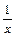 , поскольку f(х0 – 0) = –¥, f(х0 + 0) = +¥; 2) так как f(х0 + 0) = +¥, то точка х0 = 0 является точкой разрыва второго рода для функции f(x) = 3 , поскольку f(х0 – 0) = –¥, f(х0 + 0) = +¥; 2) так как f(х0 + 0) = +¥, то точка х0 = 0 является точкой разрыва второго рода для функции f(x) = 3 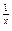 (см. рис. 1). 1.3. Непрерывность функции на промежутке Определение. Функция называется непрерывной на интервале, если она непрерывна в каждой точке этого интервала. (см. рис. 1). 1.3. Непрерывность функции на промежутке Определение. Функция называется непрерывной на интервале, если она непрерывна в каждой точке этого интервала. 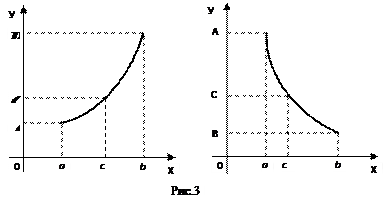 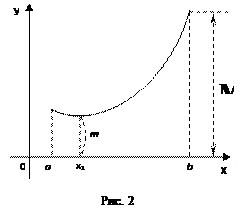 Если функция определена при х = а и при этом Если функция определена при х = а и при этом 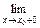 f(х) = f(а), то говорят, что f(х) в точке а непрерывна справа. Аналогично, если f(х) = f(а), то говорят, что f(х) в точке а непрерывна справа. Аналогично, если  f(х) = f(b), то говорят, что в точке b эта функция непрерывна слева. Определение. Функция называется непрерывной на отрезке [a, b], если она непрерывна в каждой его точке (в точке а непрерывна справа, в точке b – непрерывна слева). Наибольшим значением функции у = f(x) на отрезке [a, b] называется такое её значение f(x1), что f(x) £ f(x1) для всех х Î [a, b]. Наименьшим значением функции у = f(x) на отрезке [a, b] называется такое её значение f(x2), что f(x) ³ f(x2) для всех х Î [a, b]. Функции, непрерывные на отрезке, обладают рядом важных свойств, которые выражаются следующими теоремами. Теорема 1.3.1. Функция, непрерывная на отрезке [a, b], достигает на нём своего наименьшего значения m и наибольшего значения M, то есть существуют такие точки x1 и x2 этого отрезка, что f(x1) = m, f(x2) = M. Теорема имеет простой геометрический смысл (см. рис.2). Теорема 1.3.2. Если функция у = f(x) непрерывна на отрезке [a, b] и на его концах принимает неравные значения f(а) = А, f(b) = В, А ¹ В, то каково бы ни было число С, заключённое между А и В, найдётся точка с Î [a, b] такая, что f(с) = С. Геометрический смысл теоремы иллюстрируется на рис.3. Всякая прямая у = С, где A < C < B (или A > C > B), пересекает график функции у = f(x). Следствие. Если функция непрерывна на отрезке и на его концах принимает f(х) = f(b), то говорят, что в точке b эта функция непрерывна слева. Определение. Функция называется непрерывной на отрезке [a, b], если она непрерывна в каждой его точке (в точке а непрерывна справа, в точке b – непрерывна слева). Наибольшим значением функции у = f(x) на отрезке [a, b] называется такое её значение f(x1), что f(x) £ f(x1) для всех х Î [a, b]. Наименьшим значением функции у = f(x) на отрезке [a, b] называется такое её значение f(x2), что f(x) ³ f(x2) для всех х Î [a, b]. Функции, непрерывные на отрезке, обладают рядом важных свойств, которые выражаются следующими теоремами. Теорема 1.3.1. Функция, непрерывная на отрезке [a, b], достигает на нём своего наименьшего значения m и наибольшего значения M, то есть существуют такие точки x1 и x2 этого отрезка, что f(x1) = m, f(x2) = M. Теорема имеет простой геометрический смысл (см. рис.2). Теорема 1.3.2. Если функция у = f(x) непрерывна на отрезке [a, b] и на его концах принимает неравные значения f(а) = А, f(b) = В, А ¹ В, то каково бы ни было число С, заключённое между А и В, найдётся точка с Î [a, b] такая, что f(с) = С. Геометрический смысл теоремы иллюстрируется на рис.3. Всякая прямая у = С, где A < C < B (или A > C > B), пересекает график функции у = f(x). Следствие. Если функция непрерывна на отрезке и на его концах принимает 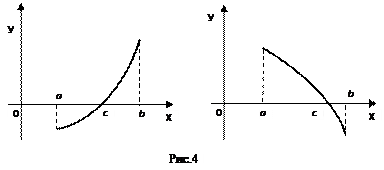 значения разных знаков, то на этом отрезке найдётся хотя бы одна точка, в которой функция обращается в нуль. Геометрический смысл следствия иллюстрируется на рис.4. Производная функции. Физический и геометрический смысл производной. Правила дифференцирования Производная функции одно из основополагающих понятий математического анализа. Мы рассмотрим основные понятия и теоремы связанные с производной функции, также обсудим геометрический и физический смысл производной функции, приведем перечень правил, которые нужно соблюдать при вычислении производной функции одной переменной и сложной функции. значения разных знаков, то на этом отрезке найдётся хотя бы одна точка, в которой функция обращается в нуль. Геометрический смысл следствия иллюстрируется на рис.4. Производная функции. Физический и геометрический смысл производной. Правила дифференцирования Производная функции одно из основополагающих понятий математического анализа. Мы рассмотрим основные понятия и теоремы связанные с производной функции, также обсудим геометрический и физический смысл производной функции, приведем перечень правил, которые нужно соблюдать при вычислении производной функции одной переменной и сложной функции. |
1. Определение производной функции.
Необходимое условие существования производной
Пусть функция 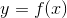 определена в точке
определена в точке 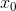 и некоторой ее окрестности. Придадим аргументу
и некоторой ее окрестности. Придадим аргументу 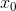 приращение
приращение 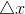 такое, что точка
такое, что точка 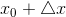 попадает в область определения функции. Функция при этом получит приращение
попадает в область определения функции. Функция при этом получит приращение 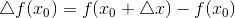 .
.
ОПРЕДЕЛЕНИЕ 1. Производной функции 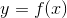 в точке
в точке 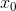 называется предел отношения приращения функции в этой точке к приращению аргумента
называется предел отношения приращения функции в этой точке к приращению аргумента 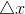 , при
, при 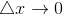 (если этот предел существует и конечен), т.е.
(если этот предел существует и конечен), т.е.
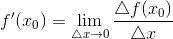 .
.
Следующая теорема устанавливает связь между существованием производной функции в точке  и непрерывностью функции в этой точке.
и непрерывностью функции в этой точке.
Теорема1. (необходимое условие существования производной функции в точке). Если функция y = f(x) имеет производную в точке  , то функция f(x) в этой точке непрерывна.
, то функция f(x) в этой точке непрерывна.
ДОКАЗАТЕЛЬСТВО
Пусть существует 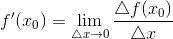 . Тогда
. Тогда
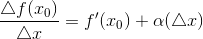 ,
,
Где 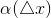 – бесконечно малая при
– бесконечно малая при  .
.
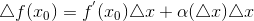 ;
;
.
Но это означает, что функция f(x) непрерывна в точке 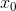 (по геометрическому определению непрерывности). ∎
(по геометрическому определению непрерывности). ∎
Замечание. Непрерывность функции в точке 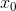 не является достаточным условием существования производной этой функции в точке
не является достаточным условием существования производной этой функции в точке 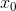 . Например, функция y = |x| непрерывна, но не имеет производной в точке
. Например, функция y = |x| непрерывна, но не имеет производной в точке 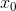 .
.
Очевидно, что соответствие 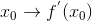 является функцией, определенной на некотором множестве
является функцией, определенной на некотором множестве 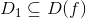 . Ее называют производной функции y = f(x) и обозначают
. Ее называют производной функции y = f(x) и обозначают
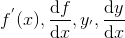 .
.
Операцию нахождения производной функции f(x) называют дифференцированием функции y = f(x).
2. Физический и геометрический смысл производной
Правила дифференцирования
1) Производная константы равна нулю, т.е 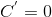 , где C – константа.
, где C – константа.
2) Производная суммы (разности) дифференцируемых функций равна сумме (разности) производных этих функций, т.е 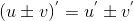 . .
. .
3) Производная произведения дифференцируемых функций находится по правилу: 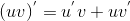 .
.
4) Константу можно выносить за знак производной : 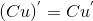 , где
, где 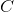 - константа.
- константа.
5) Производная дроби находится по правилу: 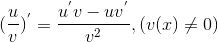 .
.
Элементы теории множеств
Понятие множества
В математике встречаются самые разнообразные множества. Можно говорить о множестве граней многогранника, точек на прямой, множестве натуральных чисел и т.д. Понятие множества относится к числу первоначальных понятий, которые не определяются через другие, более простые. Вместо слова ''множество'' иногда говорят ''совокупность'', ''собрание'' предметов и т.д. Предметы, составляющие данное множество, называются элементами данного множества.
Теория множеств посвящена в основном изучению именно бесконечных множеств. Теория конечных множеств называется иногда комбинаторикой.
Но простейшие свойства множеств, те, о которых мы только и будем здесь говорить, в большинстве случаев в равной мере относятся как к конечным, так и к бесконечным множествам.
Заметим, что в математике допускается к рассмотрению множество, не содержащее элементов – пустое множество. Запись а Î Х означает, что а есть элемент множества Х.
Определение. Множество В называется подмножеством множества А, если каждый элемент множества В является в то же время элементом множества А.
Каждый отдельный элемент множества А образует подмножество, состоящего из этого одного элемента. Кроме того, пустое множество является подмножеством всякого множества.
Подмножество множества А называется несобственным, если оно совпадает с множеством А.
Если множество В есть подмножество множества А, то говорим, что В содержится в А и обозначаем В Í А. Подмножество В множества А называется собственным подмножеством, если В не пусто и не совпадает с А (т.е. имеется элемент множества А, не содержащийся в В).
Операции над множествами
Пусть А и В – произвольные множества.
Определение. Объединением двух множеств А и В называется множество С = АÈВ, состоящее из всех элементов, принадлежащих хотя бы одному из множеств А и В. (см. рис. 1).
Аналогично определяется объединение любого (конечного или бесконечного) числа множеств: если Аi – произвольные множества, то их объединение  есть совокупность элементов, каждый из которых принадлежит хотя бы одному из множеств Аi.
есть совокупность элементов, каждый из которых принадлежит хотя бы одному из множеств Аi.
 |
Рис.1 Рис.2
Определение. Пересечением множеств А и В называется множество С = АÇВ, состоящее из всех элементов, принадлежащих как А, так и В (см. рис. 2). Пересечением любого (конечного или бесконечного) числа множеств Аi называется множество  элементов, принадлежащих каждому из множеств Аi.
элементов, принадлежащих каждому из множеств Аi.
Операции объединения и пересечения множеств по определению коммутативны и ассоциативны, т.е.
АÈВ = В È А, (А ÈВ) ÈС = А È (В È С),
А Ç В = В Ç А, (А Ç В) Ç С = А Ç (В Ç С).
Кроме того, они взаимно дистрибутивны:
(А È В) Ç С = (А Ç С) È (В Ç С), (1)
(А Ç В) È С = (А È С) Ç (В È С). (2)
Определение. Разностью множеств А и В называется множество тех элементов из А, которые не содержатся в В (рис. 3).
 |
Понятие функции. Отображение множеств
Пусть X и Y – два произвольных множества.
Определение. Говорят, что на X определена функция f, принимающая значение из Y, если каждому элементу x Î X поставлен в соответствие один и только один элемент y Î Y. При этом множество X называется областью определения данной функции, а множество Y – её областью значений.
Для множеств произвольной природы вместо термина «функция» часто пользуются термином «отображение», говоря об отображении одного множества в другое.
Если а элемент из X, то соответствующий ему элемент b = f(а) из Y называется образом а при отображении f. Совокупность всех тех элементов а из X, образом которых является данный элемент b Î Y, называется прообразом (или точнее полным прообразом) элемента b и обозначается f –1(b).
Пусть А – некоторое множество из X; совокупность {f (а): а Î А} всех элементов вида f (а), где а Î А, называется образом А и обозначается f (А). В свою очередь для каждого множества В из Y определяется его полный прообраз f –1(В), а именно: f –1(В) есть совокупность всех тех элементов из X, образы которых принадлежат В.
Определение. Будем говорить, что f есть отображение множества X на множество Y, если f (X) = Y; такое отображение называют сюръекцией. В общем случае, т.е. когда f (X) Ì Y, говорят, что f есть отображение в Y. Если для любых двух различных элементов х1 и х2 из X их образы y1 = f (x1) и y2 = f (x2) также различны, то f называется инъекцией. Отображение f: X®Y, которое одновременно является сюръекцией и инъекцией, называется взаимно однозначным соответствием междуX и Y.
