Понятие отображения (функции). Образы и прообразы множеств.

Функция (отображение, оператор, преобразование) — математическое понятие, отражающее связь между элементами множеств. Другими словами, функция — это правило, по которому каждому элементу одного множества (называемого областью определения) ставится в соответствие некоторый элемент другого множества (называемого областью значений).

Элемент y=f(x), который сопоставлен элементу x, называется образом элемента (точки) x (при отображении f).

Если взять целиком подмножество A области определения функции f, то можно рассмотреть совокупность образов всех элементов множества A, а именно подмножество области значений (функции f) вида

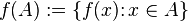которое, называется образом множества A (при отображении f). Это множество иногда обозначается как f[A] или A^f.

Наоборот, взяв некоторое подмножество B области значений функции f, можно рассмотреть совокупность тех элементов области определения (функции f), чьи образы попадают в множество B, а именно — множество вида 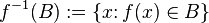которое называется (полным) прообразом множества B (при отображении f).

7. Способы задания функций. Обратная функция, сложная функция

· Табличный способ. Довольно распространенный, заключается в задании таблицы отдельных значений аргумента и соответствующих им значений функции. Такой способ задания функции применяется в том случае, когда область определения функции является дискретным конечным множеством.

· Графический способ. Графиком функции y = f(x) называется множество всех точек плоскости, координаты которых удовлетворяют данному уравнению.

· Аналитический способ. Чаще всего закон, устанавливающий связь между аргументом и функцией, задается посредством формул. Такой способ задания функции называется аналитическим.

· Словесный способ. Этот способ состоит в том, что функциональная зависимость выражается словами.

Обратная функция — функция, обращающая зависимость, выражаемую данной функцией. Например, если функция от x даёт y, то обратная ей функция от y даёт x. Чтобы найти обратную функцию, нужно решить уравнение y = f(x) относительно x. Если оно имеет более чем один корень, то функции обратной к f не существует. Таким образом, функция f(x) обратима на интервале (a;b) тогда и только тогда, когда на этом интервале она биективна.

Сложная функция – функция от функции. Если z – функция от у, т.е. z(y), а у, в свою очередь, – функция от х, т.е. у(х), то функция f(x) = z(y(x)) называется сложной функцией (или композицией, или суперпозицией функций) от х.

В такой функции х – независимая, а у – промежуточная переменная. При этом сложная функция определена для тех значений независимой переменной, для которых значения промежуточной функции у входят в область определения функции z(y).

Пусть функция g определена на множестве X и может принимать значения в множестве U. В таком случае говорят, что функция g отображает множество X в U, а сама функция записывается как

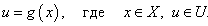
Представим теперь, что на множестве U задана другая функция f, которая отображает множество U в Y:

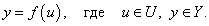
Такое двойное отображение, при котором область значений первого отображения является подмножеством области определения второго отображения, называется композицией отображений, а соответствующие функции образуют композицию функций.

Если g : X → U и f : U → Y, то композиция функций g и f обозначается как

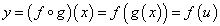
и представляет собой "двухслойную" сложную функцию или функцию от функции.

8. Числовые последовательности.

Числовой последовательностью называется числовая функция, заданная на множестве натуральных чисел или на множестве 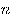первых натуральных чисел.

Для числовых последовательностей вместо 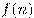обычно пишут 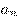, саму последовательность обозначают 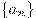, общий член последовательности обозначают 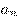. Числа 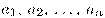называются членами последовательности: 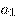— первый член последовательности, 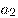— второй член последовательности, 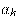— 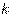-ый член последовательности и т.д.

Числовая последовательность определена, если указан закон, по которому каждому натуральному числу 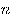ставиться в соответствие действительное число .

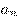Числовая последовательность может быть определена заданием ее 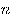-го члена формулой, позволяющей найти любой член последовательности простой подстановкой номера искомого члена в эту формулу. Такой способ задания последовательности называется явным.

Закон образования числовой последовательности может состоять в задании нескольких первых членов последовательности и рекуррентной формулы, с помощью которой каждый следующий член выражается через предыдущий (или несколько предыдущих). Такой способ задания последовательности называется рекуррентным.

Числовая последовательность называется возрастающей, если в ней каждый следующий член больше предыдущего.

Числовая последовательность называется убывающей, если в ней каждый следующий член меньше предыдущего.

Числовая последовательность называется ограниченной, если существует такое натуральное числ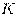о , что 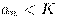для любого натурального .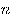