Колебания однородной бесконечной струны.

Колебания однородной бесконечной струны.

Формула Даламбера

Изучение методов построения решений краевых задач для уравнений гиперболического типа начнем с более простой задачи – задачи о свободных колебаниях однородной бесконечной струны. Это задача, как было показано в п. 1.24, сводится к решению уравнения

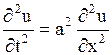(1.121)

при начальных условиях

, ,

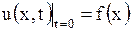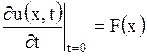(1.122)

где функции и заданы на всей числовой оси. Никакие граничные условия на искомую функцию не накладываются. Такая задача называется задачей с начальными условиями или задачей Коши.

Для решения поставленной задачи преобразуем уравнение (1.121) к каноническому виду, содержащему смешанную производную (см. (1.93)). Для чего составим уравнение характеристик

,

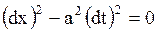которое распадается на два уравнения:

и .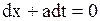

Интегрируя эти уравнения, получим

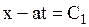и .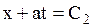

Согласно общей теории о замене переменных полагаем

, .

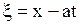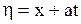Тогда уравнение (1.121) преобразуется к виду

.

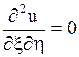Как было показано в п.1.18 (см. формулу (1.87)), общее решение такого уравнения имеет вид

,

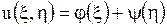где 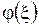и 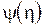- произвольные функции. Возвращаясь к старым переменным и , получим общее решение волнового уравнения (1.121)

.

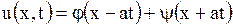(1.123)

Определим функци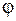и и 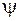таким образом, чтобы удовлетворялись начальные условия (1.122)

,

.

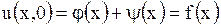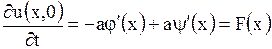Интегрируя последнее равенство по 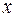, получим

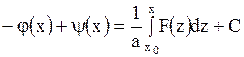, где .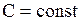

Из равенств

,

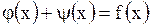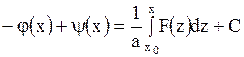
находим

,

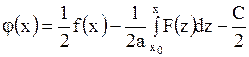(1.124)

.

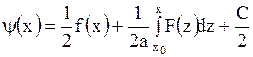(1.125)

Таким образом, мы определили функци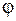и и 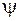через заданные функции и , причем равенства (1.124) и (1.125) имеют место для любого значения . Заменяя аргумент в (1.124) на 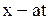, а в (1.125) на 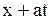и подставляя найденные функци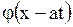и и 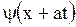в (1.123), получим

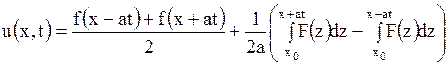
и окончательно

.

(1.126)

Формулу (1.126) называют формулой Даламбера.

Нетрудно проверить непосредственным дифференцированием, что полученное выражение для есть решение для волнового уравнения (1.121), удовлетворяющее начальным условиям (1.122). Для этого достаточно предположить, что функция дифференцируема, а функция - дважды дифференцируема. Способ вывода формулы (1.126) доказывает как единственность, так и существование решения задачи Коши. Из формулы (1.126) непосредственно видно также, что задача поставлена корректно – при любом конечном значении малому изменению функций и соответствует малое изменение решения.

РЕШЕНИЕ УРАВНЕНИЯ КОЛЕБАНИЙ СТРУНЫ МЕТОДОМ ХАРАКТЕРИСТИК (МЕТОДОМ ДАЛАМБЕРА)

Одним из широко используемых способов решения уравнений колебаний струны является метод характеристик, называемый методом Даламбера. В основе его лежит тот факт, что с помощью замены 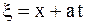, 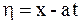уравнение

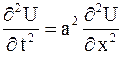(2.73)

преобразуется в уравнение 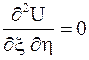, которое имеет общее решение

,

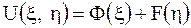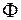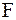где и - произвольные дважды дифференцируемые функции (см. пример 2.40). Для определения функци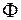й и 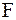, т.е. для определения закона колебаний струны, требуется использовать начальные условия, а для некоторых задач и граничные. Если вернуться к старым переменным 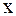и 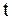, то общее решение примет вид

.

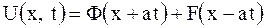Здесь 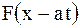характеризует прямую волну (кривая 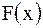смещается вправо со скоростью 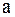), а 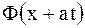- обратную волну (кривая 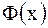смещается влево со скоростью ).

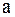Если рассматривается задача Коши для бесконечной струны 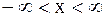, то по заданным начальным условиям

,

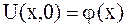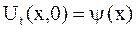(2.74)

определяются функци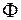и и 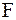, и искомое решение имеет вид

.

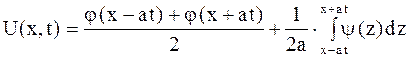(2.75)

Формула (2.75) называется формулой Даламбера. Эта формула доказывает единственность решения задачи Коши.

В частности, когда начальная скорость равна нулю ( 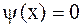), то

,

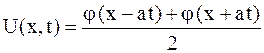откуда легко вычислить отклонение струны от положения равновесия для любой из ее точек; оно равно сумме левой и правой бегущих волн, причем начальная форма каждой волны определяется функцией 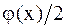, равной половине начального отклонения.

В случае полубесконечной струны, кроме начальных условий (2.74), заданных при 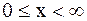, необходимо добавить еще граничное условие (конец предполагается в точке )

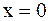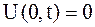(2.76)

для закрепленной в точке 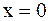струны,

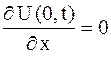(2.77)

для свободного конца в точке ,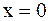

.

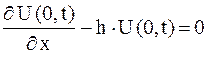для упругого закрепления в точке .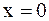

В случае однородных граничных условий (2.76) или (2.77) решение задачи о колебании полубесконечной струны сводится к решению задачи о колебании бесконечной струны путем продолжения начальных условий на всю ось нечетным образом для условия (2.76), т.е. полагают 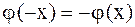, , 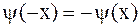и четным образом для условия (2.77), т.е. , .

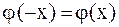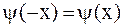Примеры решения задач

ПРИМЕР 2.43. Найти форму достаточно длинной струны, определяемой уравнением 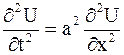, в момент времени 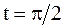, , 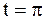если заданы начальные смещения и скорости:

а) ;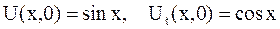

б) ;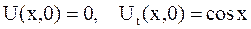

в) .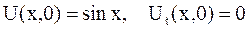

Решение. По постановке вопроса надо найти решение 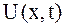задачи Коши (2.73), (2.74) в области: 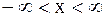, 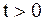. Оно определяется формулой Даламбера (2.75).

Случай а). Полагая в формуле Даламбера 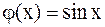, , 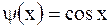найдем смещение 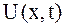в любой точке и любой момент :

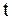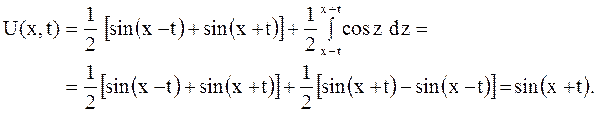
Откуда определяем форму кривой в указанные моменты времени:

, .

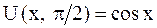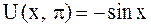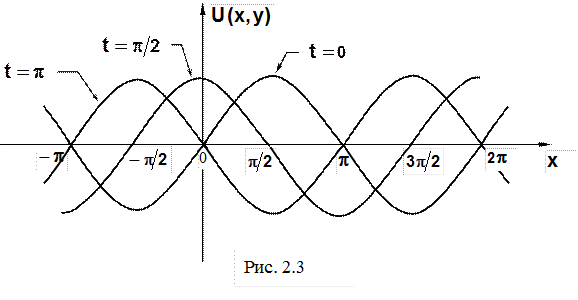
Кривые изображены на рис. 2.3.

Случай б) Начальные смещения струны равны нулю, т.к. 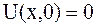. При 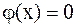колебательный процесс будет описан по формуле

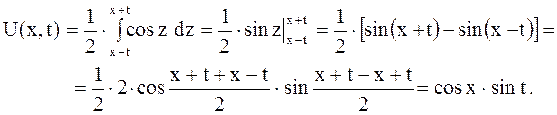
В момент времени 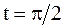струна имеет форму косинусоиды: 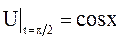, а в момент 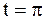она совпадает с осью абсцисс: .

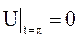Случай в). По условию, начальные скорости равны нулю, значит, 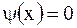. Тогда имеем

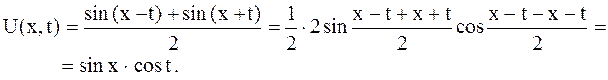
Форма струны в указанные моменты времени определяется уравнениями:

, .

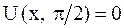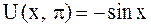РЕШЕНИЕ УРАВНЕНИЯ КОЛЕБАНИЙ СТРУНЫ МЕТОДОМ ХАРАКТЕРИСТИК (МЕТОДОМ ДАЛАМБЕРА)

Одним из широко используемых способов решения уравнений колебаний струны является метод характеристик, называемый методом Даламбера. В основе его лежит тот факт, что с помощью замены 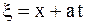, 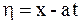уравнение

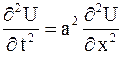(2.73)

преобразуется в уравнение 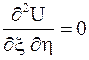, которое имеет общее решение

,

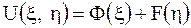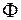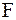где и - произвольные дважды дифференцируемые функции (см. пример 2.40). Для определения функци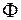й и 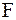, т.е. для определения закона колебаний струны, требуется использовать начальные условия, а для некоторых задач и граничные. Если вернуться к старым переменным 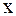и 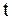, то общее решение примет вид

.

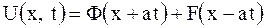Здесь 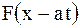характеризует прямую волну (кривая 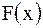смещается вправо со скоростью 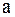), а 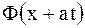- обратную волну (кривая 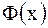смещается влево со скоростью ).

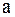Если рассматривается задача Коши для бесконечной струны 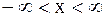, то по заданным начальным условиям

,

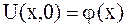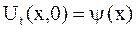(2.74)

определяются функци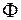и и 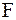, и искомое решение имеет вид

.

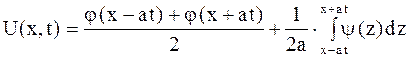(2.75)

Формула (2.75) называется формулой Даламбера. Эта формула доказывает единственность решения задачи Коши.

В частности, когда начальная скорость равна нулю ( 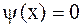), то

,

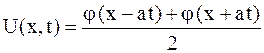откуда легко вычислить отклонение струны от положения равновесия для любой из ее точек; оно равно сумме левой и правой бегущих волн, причем начальная форма каждой волны определяется функцией 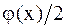, равной половине начального отклонения.

В случае полубесконечной струны, кроме начальных условий (2.74), заданных при 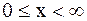, необходимо добавить еще граничное условие (конец предполагается в точке )

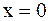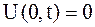(2.76)

для закрепленной в точке 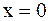струны,

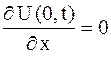(2.77)

для свободного конца в точке ,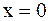

.

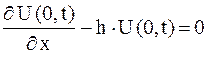для упругого закрепления в точке .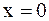

В случае однородных граничных условий (2.76) или (2.77) решение задачи о колебании полубесконечной струны сводится к решению задачи о колебании бесконечной струны путем продолжения начальных условий на всю ось нечетным образом для условия (2.76), т.е. полагают 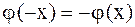, , 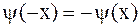и четным образом для условия (2.77), т.е. , .

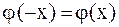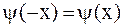Примеры решения задач

ПРИМЕР 2.43. Найти форму достаточно длинной струны, определяемой уравнением 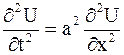, в момент времени 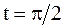, , 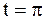если заданы начальные смещения и скорости:

а) ;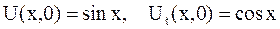

б) ;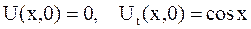

в) .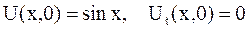

Решение. По постановке вопроса надо найти решение 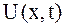задачи Коши (2.73), (2.74) в области: 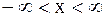, 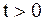. Оно определяется формулой Даламбера (2.75).

Случай а). Полагая в формуле Даламбера 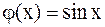, , 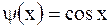найдем смещение 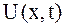в любой точке и любой момент :

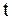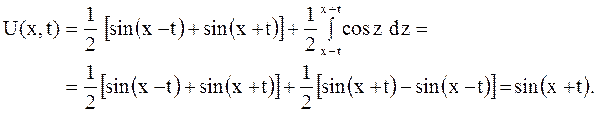
Откуда определяем форму кривой в указанные моменты времени:

, .

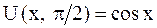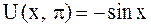Кривые изображены на рис. 2.3.

Случай б) Начальные смещения струны равны нулю, т.к. 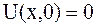. При 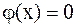колебательный процесс будет описан по формуле

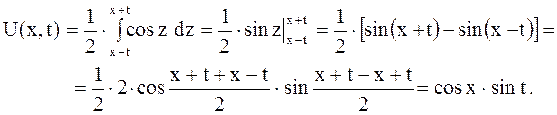
В момент времени 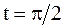струна имеет форму косинусоиды: 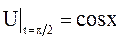, а в момент 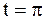она совпадает с осью абсцисс: .

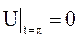Случай в). По условию, начальные скорости равны нулю, значит, 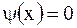. Тогда имеем

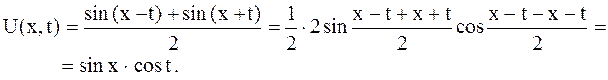
Форма струны в указанные моменты времени определяется уравнениями:

, .

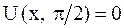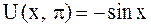Колебания однородной бесконечной струны.

Формула Даламбера

Изучение методов построения решений краевых задач для уравнений гиперболического типа начнем с более простой задачи – задачи о свободных колебаниях однородной бесконечной струны. Это задача, как было показано в п. 1.24, сводится к решению уравнения

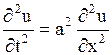(1.121)

при начальных условиях

, ,

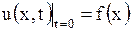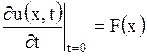(1.122)

где функции и заданы на всей числовой оси. Никакие граничные условия на искомую функцию не накладываются. Такая задача называется задачей с начальными условиями или задачей Коши.

Для решения поставленной задачи преобразуем уравнение (1.121) к каноническому виду, содержащему смешанную производную (см. (1.93)). Для чего составим уравнение характеристик

,

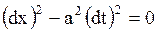которое распадается на два уравнения:

и .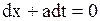

Интегрируя эти уравнения, получим

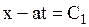и .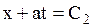

Согласно общей теории о замене переменных полагаем

, .

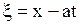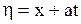Тогда уравнение (1.121) преобразуется к виду

.

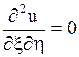Как было показано в п.1.18 (см. формулу (1.87)), общее решение такого уравнения имеет вид

,

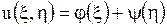где 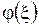и 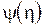- произвольные функции. Возвращаясь к старым переменным и , получим общее решение волнового уравнения (1.121)

.

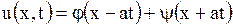(1.123)

Определим функци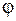и и 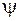таким образом, чтобы удовлетворялись начальные условия (1.122)

,

.

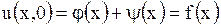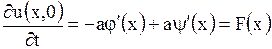Интегрируя последнее равенство по 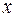, получим

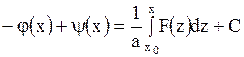, где .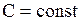

Из равенств

,

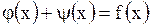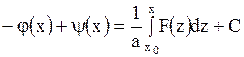
находим

,

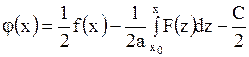(1.124)

.

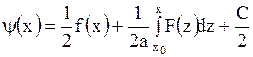(1.125)

Таким образом, мы определили функции и 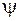через заданные функции и , причем равенства (1.124) и (1.125) имеют место для любого значения 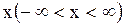. Заменяя аргумент в (1.124) на 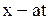, а в (1.125) на 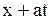и подставляя найденные функци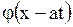и и 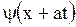в (1.123), получим

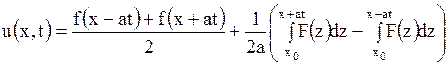
и окончательно

.

(1.126)

Формулу (1.126) называют формулой Даламбера.

Нетрудно проверить непосредственным дифференцированием, что полученное выражение для есть решение для волнового уравнения (1.121), удовлетворяющее начальным условиям (1.122). Для этого достаточно предположить, что функция дифференцируема, а функция - дважды дифференцируема. Способ вывода формулы (1.126) доказывает как единственность, так и существование решения задачи Коши. Из формулы (1.126) непосредственно видно также, что задача поставлена корректно – при любом конечном значении малому изменению функций и соответствует малое изменение решения.