Исследование динамических свойств типовых звеньев сау во временной и частотной областях

Цель работы – анализ переходных и частотных характеристик важнейших типовых звеньев систем автоматического управления.

Основные сведения

Переходная характеристика (ПХ) динамического звена (или системы) – это его реакция 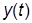на единичное ступенчатое входное воздействие 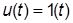при нулевых начальных условиях (ННУ). Для ПХ обычно используют специальное обозначение 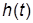. Передаточной функцией (ПФ) звена называют отношение изображения по Лапласу выходной и входной переменных этого звена при ННУ: .

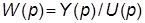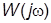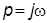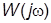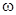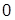Частотная передаточная функция (ЧПФ) получается из ПФ подстановкой . Годограф функции при изменении аргумента от до 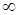называется амплитудно-фазовой частотной характеристикой (АФХ). Если ЧПФ представлена в показательной форме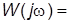 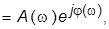то функции 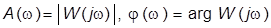называются, соответственно, амплитудной (АЧХ) и фазовой (ФЧХ) частотными характеристиками. Они характеризуют поведение устойчивого звена (системы) в установившемся режиме при гармоническом входном воздействии и могут быть определены экспериментально. Для этого на вход исследуемого звена необходимо подавать гармоническое воздействие постоянной амплитуды и различной частоты. Тогда установившаяся реакция звена на это воздействие будет также гармонической функцией той же частоты, но, вообще говоря, другой амплитуды и с фазовым сдвигом относительно входной гармоники. Отношение амплитуд выходной и входной гармоник на каждой заданной частоте равно значению АЧХ, а относительный фазовый сдвиг этих функций – значению ФЧХ на указанной частоте.

Функция 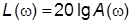называется логарифмической амплитудной частотной характеристикой (ЛАХ) и графически изображается как функция частоты 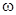, рад/c, откладываемой по оси абсцисс в логарифмическом масштабе, т. е. фактически как функция безразмерной переменной 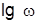, откладываемой в равномерном масштабе. Значения 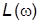измеряются в децибелах (дБ) и откладываются по оси ординат в равномерном масштабе. ФЧХ, изображаемая как функция частоты, откладываемой в логарифмическом масштабе, называется логарифмической фазовой частотной характеристикой (ЛФХ). Ее значения измеряются в градусах или радианах. ЛАХ и ЛФХ называются логарифмическими частотными характеристиками (ЛЧХ).

Программа работы

1. Задать интегрирующее звено с передаточной функцией 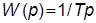, взяв значение 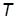из табл. 1.1 (номер варианта задает преподаватель).

2. Выполнить анализ характеристик звена и ответить на приведенные вопросы.

а) Чему равно значение ПХ 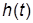при ?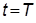

б) Что представляют собой графики ЛАХ и ЛФХ ?

в) На какой частоте ЛАХ пересекает ось абсцисс ?

г) Как изменятся ПХ и ЛАХ при увеличении значения 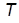вдвое ?

3. Задать апериодическое звено первого порядка с ПФ 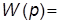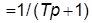, взяв то же значение 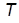, что и в п. 1.

4. По результатам анализа ответить на приведенные вопросы.

а) Чему равно значение ?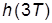

б) Каков полюс ПФ ?

в) Каковы значения ЛАХ и ЛФХ на частотах 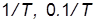и ?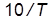

г) Как изменятся значения ПХ и ЛЧХ при уменьшении значения 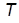в 2 раза ? Что при этом произойдет с АФХ ?

д) Как изменятся значения ПХ и ЛЧХ при увеличении коэффициента передачи в 2 раза ?

5. Задать неустойчивое апериодическое звено первого порядка с ПФ 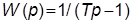, назначив значение 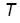в соответствии с п. 1.

6. На основании анализа ПХ, ЛАХ, ЛФХ, АФХ, полюса ПФ дать характеристику различий в свойствах звеньев, заданных в пп. 3 и 5.

7. Задать колебательное звено с ПФ 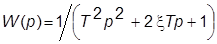с параметрами из табл. 1.1.

Таблица 1.1

Параметр	Вариант
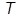, с	0.1	0.2	0.25	0.4	0.5	0.8	1.0	1.25	1.6	2.0
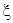	0.4	0.3	0.25	0.2	0.1	0.08	0.06	0.05	0.04	0.03

8. Выполнить анализ характеристик звена и ответить на приведенные вопросы.

а) Как влияет на показатель качества ПХ (максимальное значение, длительность переходного процесса, период колебаний) уменьшение коэффициента затухания 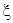в 5 раз по сравнению с заданным?

б) Как повлияет на эти же показатели уменьшение постоянной времени 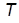в 2 раза ?

в) Как меняется картина расположения полюсов передаточной функции при изменени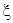и и ?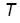

г) Что происходит с высотой резонансного пика ЛАХ при уменьшении 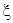и с резонансной частотой 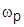при уменьшении ?

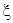9. Увеличить значение 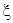до произвольного значения, большего или равного единице, превратив тем самым звено в апериодическое звено второго порядка. Описать изменения, произошедшие с ПХ и с расположением полюсов на комплексной плоскости.

10. Определить путем имитации реального эксперимента значения АЧХ (ЛЧХ) и ФЧХ (ЛФХ) апериодического звена (значение 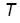взять из табл.1.1) при трех значениях частоты 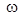: 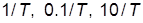. Рекомендуется воспользоваться следующей последовательностью действий:

· на вход исследуемого звена подать гармонический сигнал единичной амплитуды и заданной частоты;

· определить амплитуду выходного сигнала 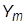и его временной сдвиг 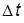относительно входного; указанные измерения следует производить по прошествии интервала времени не менее 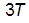, когда наблюдаемый на выходе звена процесс можно считать установившимся; удобно совместить в одном окне входной и выходной процессы с помощью мультиплексора;

· определить значения АЧХ и ФЧХ как 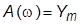и 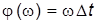, а также вычислить ;

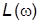· полученные для каждого значения частоты данные занести в таблицу.

11. Описанным в предыдущем пункте способом определить значения АЧХ (ЛЧХ) и ФЧХ (ЛФХ) колебательного звена с параметрами, взятыми из табл. 1.1, при указанных значениях частоты.

Содержание отчета

1. Ответы на вопросы, содержащиеся в программе работы.

2. Результаты экспериментального определения АЧХ и ФЧХ (и, соответственно, ЛЧХ и ЛФХ) апериодического и/или колебательного звеньев. Изобразить теоретические графики асимптотических ЛАХ рассматриваемых звеньев и нанести на них точки, определенные экспериментально, а также в 4, в). Прокомментировать результаты.

Контрольные вопросы

1. Дайте определения передаточной функции, частотной передаточной функции, АЧХ, ФЧХ, ЛАХ, ЛФХ звена (системы).

2. Каков "физический смысл" АЧХ и ФЧХ (с точки зрения реакции на гармоническое воздействие)?

3. Зависит ли точность экспериментального определения АЧХ и ФЧХ от интервала наблюдения?

4. Выведите аналитические выражения для переходных характеристик интегрирующего и апериодического звеньев.

5. Каков "физический смысл" постоянной времени интегрирующего звена?

6. Укажите максимальное число способов определения постоянной времени апериодического звена по графику его переходной характеристики.

7. Как связаны полюсы ПФ колебательного звена с поведением огибающей его переходной характеристики и частотой колебаний?

8. Выведите аналитическую зависимость между значением ЛАХ колебательного звена на частоте 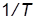и коэффициентом затухания .

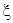Лабораторная работа № 2