Координатах и координатах ротора

Математическая модель синхронного генератора (СГ) включает систему уравнений, описывающих электрические процессы в генераторе и механические процессы, вызванные взаимодействием генератора и приводного двигателя (обычно – дизеля).

Основой для составления уравнений электрической части является конструкция СГ с размещенными в нем катушками обмоток статора и ротора (рис.2.1).

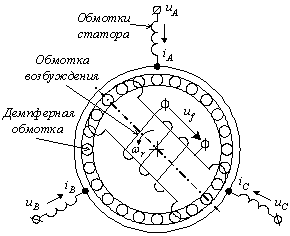
Рисунок 2.1 - Конструкция синхронного генератора

К обмотке возбуждения подведено постоянное напряжение u_f возбуждения.

Демпферная обмотка конструктивно представляет собой "беличье колесо".

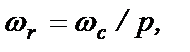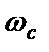Ротор приводится во вращение дизелем. Частота вращения ротора равна где - частота напряжения сети, р – число пар полюсов обмотки статора. Вращающимся магнитным полем обмотки возбуждения в обмотках статора наводится э.д.с., а на выводах обмоток устанавливается трехфазное переменное напряжение

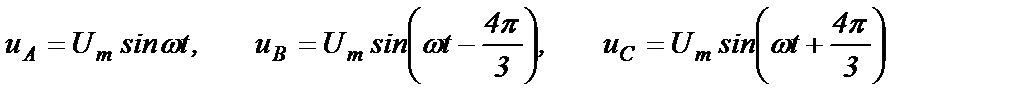(2.1)

При подключении к статорным обмоткам электрической нагрузки по обмоткам протекают токи i_A, i_B и i_C, которые создают вращающееся магнитное поле статора. Частота вращения _s поля статора совпадает в установившемся режиме с частотой вращения ротора _r. Взаимодействие магнитных полей статора и ротора создает электромагнитную силу, которая направлена против силы, приложенной к ротору со стороны дизеля.

Электрическая схема СГ представляет собой схему катушек (рис.2.2).

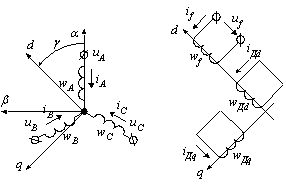
Рисунок 2.2 - Схема обмоток синхронного генератора

Обмотки статора на рис.2.2 в точности повторяют обмотки статора, изображенные на рис.2.1. Для этих обмоток вводится неподвижная относительно их система осей , причем ось  совпадает с осью обмотки фазы А, а ось  опережает ось  на 90^о.

На роторе обмотка возбуждения (индекс f) в точности соответствует физической обмотке, изображенной на рис.2.1. Для ротора вводятся оси d-q, причем ось d совпадает с осью обмотки возбуждения, а ось q опережает ось d на угол 90^о. Следовательно, оси d-q вращаются в месте с ротором и обмотки ротора неподвижны относительно этих осей.

Физическая демпферная обмотка ("беличье колесо") заменена на две взаимно-перпендикулярные обмотки, ориентированные по осям d и q, с числом витков w_Дd и w_Дq. С помощью введенных двух демпферных обмоток в принципе можно создать такое же магнитное поле, какое создает физическая демпферная обмотка. Преимущество представления демпферной обмотки в виде двух обмоток состоит в том, что сокращается до двух число дифференциальных уравнений, с помощью которых описываются электрические процессы в этой обмотке (для физической демпферной обмотки число таких уравнений было бы больше двух, так как "беличья клетка" содержит десятки короткозамкнутых контуров).

За счет вращения ротора между осями d и  образуется угол , изменяющийся по закону

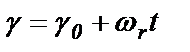(2.2)

Величина скольжения для СГ определяется выражением

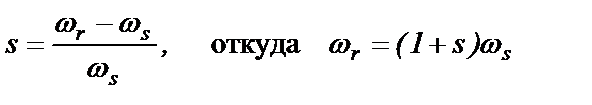(2.3)

Каждая из катушек, изображенная на рис.2.2, может быть описана дифференциальным уравнением типа

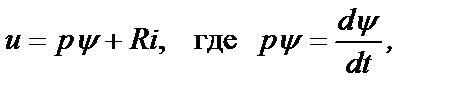(2.4)

а y - потокосцепление катушки.

Для катушек на рис.2.2 имеем систему дифференциальных уравнений

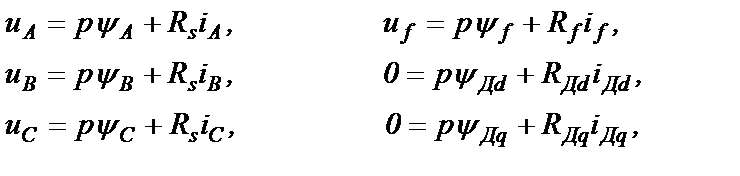(2.5)

где R_s, R_f, R_Дd и R_Дq – активные сопротивления обмоток, соответственно, статора, возбуждения и демпферов по осям d и q;

р – символ производной.

Достоинство системы уравнений (2.5) в том, что она получена из простейшей модели СГ, представленной на рис.2.2. Однако недостатков такого описания СГ очень много.

Первый недостаток - система уравнений нелинейная. Нелинейность заложена в формулах, по которым рассчитываются потокосцепления обмоток. Для доказательства указанной нелинейности рассчитаем потокосцепление, например, обмотки фазы А статора.

Потокосцепление фазы А

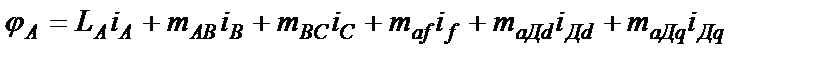(2.6)

складывается из потокосцеплений, создаваемых собственным током i_A фазы А статора, токами i_В и i_С фаз В и С статора, током i_f обмотки возбуждения и токами i_Дd и i_Дq демпферной обмотки.

Как индуктивность L_A фазы А, так и все коэффициенты m взаимной индукции обмотки фазы А со всеми остальными обмотками СГ изменяются во времени. Следовательно, произведения токов на индуктивность и коэффициенты взаимной индукции являются нелинейными величинами.

Для примера докажем изменение во времени коэффициента взаимоиндукции m_af обмотки фазы А с обмоткой возбуждения (рис.2.3,а,б). В положении а) зазор δ минимален и, поэтому, максимальное количество линий магнитного потока обмотки возбуждения проходит через площадь витков катушки фазы А. Поэтому m_af= m_afmax. В положении б) зазор δ максимален, между осями обмоток угол прямой и, поэтому, магнитный поток возбуждения вообще не проходит через площадь, охваченную витками катушки А. Поэтому m_af=0. При произвольном угле  между осями обмоток фазы А и возбуждения коэффициент взаимной индукции m_af определится выражением

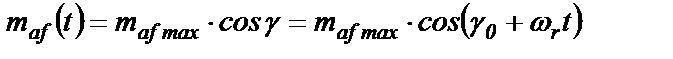(2.7)

Рассчитаем еще коэффициент взаимной индукции m_АВ между фазными обмотками А и В статора (рис.2.4,а,б). В положении а), когда =30^о, магнитная связь между обмотками самая сильная m_АВ= m_АВmax, так как на пути магнитного потока, связывающего обе обмотки, находится максимальный объем (масса) стали ротора. В положении б), когда =120^о, магнитная связь между обмотками самая слабая m_АВ= m_АВmin, так как на пути магнитного потока, связывающего обе обмотки, находится минимальный объем (масса) стали ротора. При произвольном угле  между осями обмоток фазы А и возбуждения коэффициент взаимной индукции m_AB определится выражением

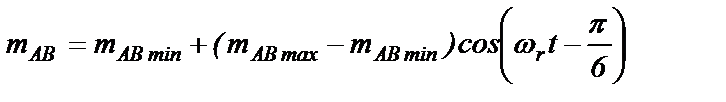(2.8)

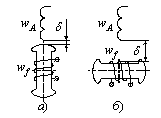
Рисунок 2.3 - Взаимная индукция между обмотками фазы А статора и возбуждения

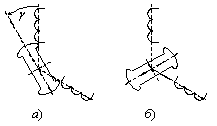
Рисунок 2.4 - Взаимная индукция между обмотками фаз А и В статора

Второй недостаток - входящие в систему (2.5) сигналы напряжений u_A, u_B и u_C изменяются по синусоидальном законам с частотой _c, а потокосцепления ротора изменяются с частотой _r, что следует из выражений (2.7, 2.8). Даже одно это в случае линейности уравнений системы (2.5) создает большие сложности в определении частных решений системы.

Отмеченные сложности математического описания СГ вытекают непосредственно из принятой для описания электрической схемы СГ в виде, приведенном на рис.2.2. Поэтому в теории переходных процессов СГ применяется схема катушек в виде, приведенном на рис.2.5, со следующими особенностями:

1) для статора и ротора используются единые оси d-q, которые жестко связаны с обмотками ротора;

2) физический статор с тремя обмотками, которые неподвижны относительно осей α-β, заменен на модельный статор, состоящий из двух взаимно перпендикулярных обмоток w_d и w_q, которые неподвижны относительно ротора, т.е. модельные обмотки w_d и w_q статора вращаются синхронно с ротором;

3) введенные обмотки статора получают питание не из сети, а от некоторого источника переменных напряжений u_d и u_q.

Обоснование этих замен следующее.

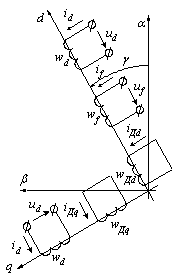
Рисунок 2.5 - Схема обмоток СГ в осях d и q ротора

С помощью двух введенных обмоток статора, расположенных по осям d и q, можно создать такое по величине и направлению магнитное поле, которое тождественно магнитному полю трехфазной обмотки статора, если соответствующим образом подобрать по величине и закону изменения во времени напряжения питания u_d и u_q обмоток w_d и w_q. Следовательно, все энергетические характеристики взаимодействия ротора и статора в модельном СГ будут такими же, как и в физическом СГ. Электрические характеристики модельного СГ, могут быть пересчитаны в характеристики физического СГ.

При представлении СГ в виде схемы на рис.2.5 обмотки статора и ротора оказываются друг относительно друга неподвижными и, следовательно, коэффициенты взаимоиндукции и индуктивности всех обмоток становятся постоянными величинами. Поэтому дифференциальные уравнения (2.5) превращаются в линейные. В этом состоит положительный эффект от перехода к схеме СГ на рис.2.5.

Покажем на частных случаях то, как могут быть определены напряжения u_d и u_q в схеме на рис.2.5.

Пусть в физическом СГ ротор вращается синхронно с магнитным полем статора, опережая поле статора на угол нагрузки q (угол нагрузки q - это также угол между обобщенным вектором напряжения u статора и вектором э.д.с. e_f, наводимой в обмотках статора вращающимся магнитным полем _f обмотки возбуждения). Тогда будут неподвижны друг относительно друга магнитные поля статора, создаваемые токами i_d и i_q, и ротора, создаваемый током i_f. В модельном СГ будут те же поля при питании обмотки возбуждения постоянным напряжением u_f, а обмоток статора – постоянными напряжениями

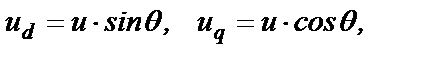(2.9)

где u – амплитуда напряжения питания статора модельного СГ.

Система уравнений (2.5) будет линейной с постоянными по величине входными сигналами. Такую систему можно решить аналитически.

Пусть в физическом СГ ротор вращается не синхронно с магнитным полем статора. Тогда их относительная частота вращения будет равна частоте скольжения

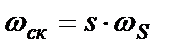(2.10)

На модельном СГ те же поля могут быть получены при подаче на обмотку возбуждения постоянного напряжения u_f, а на обмотки статора – двух гармонических напряжений u_d и u_q, сдвинутых друг относительно друга на 90^о, изменяющихся с частотой скольжения _ск.

Таким образом, показана принципиальная возможность получения на модели СГ таких же магнитных полей статора и ротора, как и в физическом генераторе.

Вопросы для самоконтроля

1. Поясните конструкцию синхронного генератора и сигналы в ней.

2. Поясните схему обмоток синхронного генератора в физических осях и сигналы в ней.

3. Приведите уравнения обмоток синхронного генератора и поясните их достоинства и недостатки.

4. Поясните схему обмоток синхронного генератора в осях ротора и сигналы в ней.

Литература [1-9]