Дифференциальных уравнений в нормальной форме. Расчеты начальных условий

Часто объект исследования описывается не одним дифференциальным уравнением типа (1.27) или (1.29), а системой уравнений низкого порядка. Среди указанной системы могут быть как дифференциальные уравнения, так и алгебраические уравнения. Эта ситуация также характерна для автоматических систем, где принято изображение их в виде структурной схемы соединения отдельных блоков, причем каждый блок описывается передаточной функцией. Также на практике характерна ситуация, когда на некоторые переменные накладываются ограничения на минимальное и максимальное значения.

Рассмотрим на примере приведение описания объекта исследования в виде системы уравнений в нормальной форме. Исходными данными являются:

- структурная схема САУ и передаточные функции звеньев (рис.1.12);

- начальные условия для сигналов блоков структурной схемы, передаточная функция которых содержит производную (символ производной р).

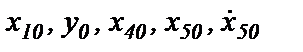(1.49)

Типовые передаточные функции звеньев, которые могут встретиться в расчетах, приведены на рисунке. Передаточные функции произвольного написания необходимо привести к форме, указанной на рисунке, когда коэффициент при р будет равен единице. Например, если передаточная функция некоторого звена имеет вид 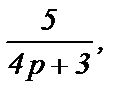то, поделив числитель и знаменатель на 4 (коэффициент при р), получим .

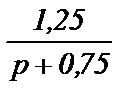Звено второго порядка может быть заменено приближенным звеном первого порядка при следующих условиях

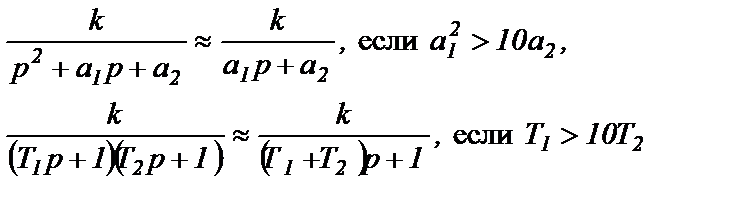
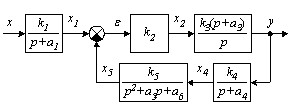
Рисунок 1.12 - Структурная схема САУ

Приведение описания САУ системой дифференциальных уравнений, записанных в нормальной форме, состоит из следующих этапов (табл.1.2):

1. Составляем систему операторных уравнений (столбец 1 табл.1.2), используя выражения передаточных функций звеньев, в т.ч. и элемента сравнения, и обозначения сигналов, проставленные на структурной схеме САУ.

2. Приводим составленные уравнения к нормальной форме, в которой каждое дифференциальное уравнение содержит в левой части только 1-ю производную только от одной переменной, а в правой – произвольную функцию от всех переменных. Сначала приведение к нормальной форме выполняем путем простых переносов членов дифференциальных уравнений с одной части в другую (столбец 2 табл.1.2). Алгебраические уравнения системы преобразовывать не надо.

3. Преобразуем оставшиеся уравнения к нормальной форме. Во втором столбце табл.1.2 таких дифференциальных уравнений два - в 4-й и 6-й строках.

В 4-м уравнении содержатся производные в левой и правой частях. Преобразуем его в нормальную форму с помощью алгебраической подстановки

у=у₁+с₁x₂,

где у₁ – новая переменная;

с₁ – коэффициент, значение которого должно быть таким, чтобы после применения указанной подстановки в правой части уравнения не было бы производной.

Тогда преобразования 4-го уравнения будут следующими:

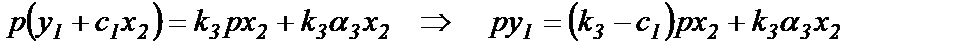
Чтобы в правой части была сокращена производная первого порядка, необходимо принять с₁=k₃. Тогда дифференциальное уравнение примет вид

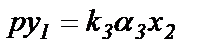
В целом 4-е уравнение 2-го столбца будет эквивалентно системе, состоящей из алгебраического и дифференциального уравнений,

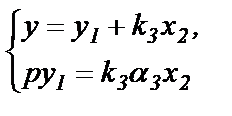(1.50)

Уравнения системы (1.50) занимают строчки 4 и 5 в 3-м столбце табл.1.2.

Таблица1.2

Этапы приведения описания САУ к нормальной форме

1-й этап	2-й этап	3-й этап

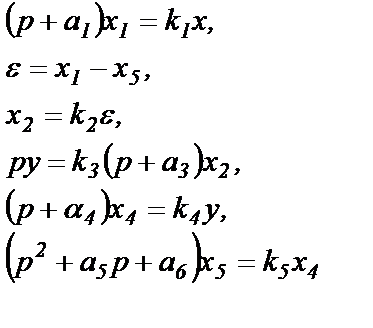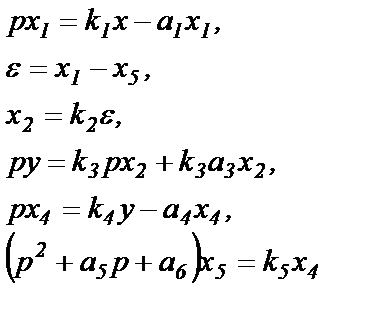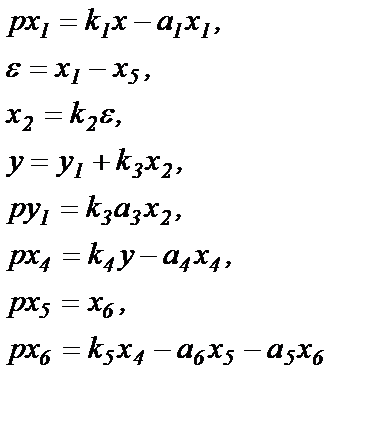Для шестого уравнения 2-го столбца применяем дифференциальную подстановку

px₅=x₆

С этой подстановкой 6-е уравнение 2-го столбца будет эквивалентно системе из двух дифференциальных уравнений

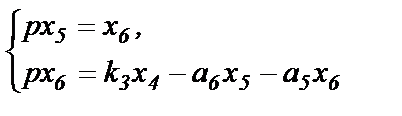(1.51)

Уравнения системы (1.51) занимают две последних строчки 3-м столбце табл.1.2.

Теперь все дифференциальные уравнения системы, приведенные в 3-м столбце табл.1.2, представлены в нормальной форме.

4. Далее все уравнения 3-го столбца приводим к виду, который необходим для их решения численными методами на компьютере. В табл.1.3 приведено соответствие машинных переменных Y₀…Y₅ физическим переменным х₁, у₁, х₄, х₅ и х₆, от которых взяты производные. Машинные переменные быть индексными переменными.

Таблица 1.3

Соответствие машинных и физических переменных

Машинные переменные	Y0	Y1	Y2	Y3	Y4
Физические переменные	х1	у1	х4	х5	х6

Система уравнений вводится для счета в форме

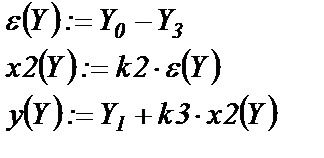Алгебраические выражения (1.52)

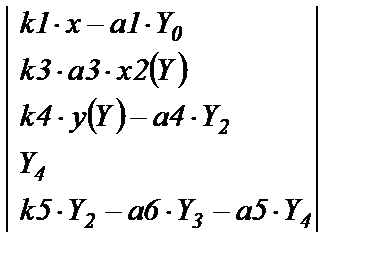
(1.53)

5. Рассчитываем начальные условия для машинных переменных Y₀…Y₅. на основе начальных условий (1.49) для физических сигналов схемы САУ.

Согласно табл.1.3

Y₀≡x₁, Y₁≡y₁, Y₂≡x₄, Y₃≡x₅, Y₄≡x₆ (1.54)

Из пяти, стоящих в правой части тождеств (1.54) переменных, только для трех переменных х₁, х₄ и х₅ заданы начальные условия (1.49). Поэтому для переменных Y₀, Y₂, и Y₃ начальные условия определяются без всякого вычисления, а простым присвоением:

Y₀₀=х₁₀, Y₂₀=х₄₀, Y₃₀=х₅₀ (1.55)

В соответствии с предпоследним уравнением системы, прописанной в 3-м столбце табл.1.2, имеем

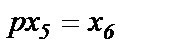или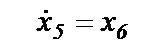

Согласно (1.54) Y₄≡x₆ и согласно (1.49) задано начальное условие 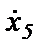. Поэтому, для переменной Y₄ начальным условием будет

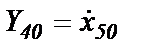(1.56)

В соответствии 2-м, 3-м и 4-м уравнениями системы, прописанной в 3-м столбце табл.1.2, имеем

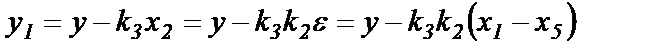
Поэтому начальным условием для Y₁≡y₁ будет

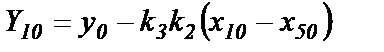(1.57)

Достоинствами метода приведения описания ЭМС, заданного в виде структурной схемы, к системе дифференциальных уравнений в нормальной форме являются:

1. Простой расчет начальных условий, так как большинство машинных переменных являются физическими, а для них начальные условия естественно являются известными.

2. Мал объем преобразований и вычислений в сравнении с ранее рассмотренным методом приведения одного дифференциального уравнения высокого п-го порядка к нормальной форме, перед применением которого нужно было свернуть структурную схему САУ (рис.1.12).

Если для математического моделирования используется пакет MathCAD, то данные для программы моделирования должны быть представлены в виде

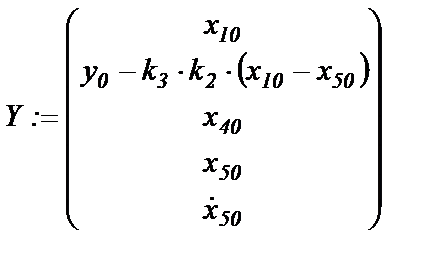
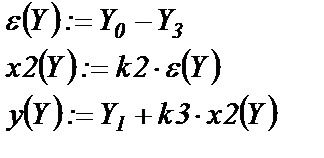
Матрица начальных условий Алгебраические выражения

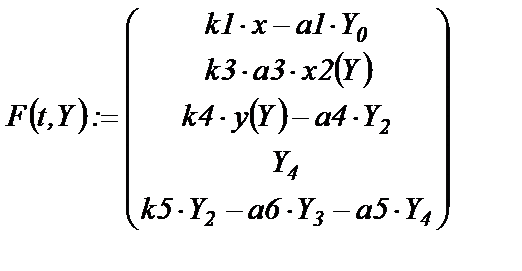
Матрица уравнений в нормальной форме

Вопросы для самоконтроля

1. Какая должна быть проведена подготовка передаточных функций звеньев структурной схемы САУ перед выводом системы дифференциальных уравнений в нормальной форме?

2. Поясните содержание действий на 1-м и 2-м этапах вывода системы уравнений в нормальной форме для САУ заданной структурной схемой.

3. Поясните содержание действий на 3-м этапе вывода системы уравнений в нормальной форме для САУ заданной структурной схемой.

4. Поясните вид уравнений в машинных переменных.

5. Поясните процедуры определения начальных условий для машинных переменных.

Литература [1-9]