Построение прямого кругового конуса
Развертка поверхности прямого кругового конуса представляет собой плоскую фигуру, состоящую из кругового сектора и круга. Построение выполняют следующим образом. Проводят осевую линию и из точки, взятой на ней, как из центра, радиусом равным образующей конуса, очерчивают дугу окружности.
Развертка конической поверхности выполняется аналогично развертке пирамиды, предварительно вписав в конус n-угольную пирамиду (рис.7)[5 с. 11].
Построение конуса
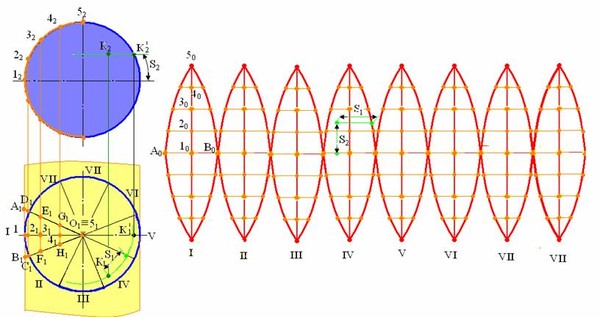
Развертку конуса вращения строят так же, как и развертку пирамиды.Делят окружность основания на равные части, например на 12 частей, и представляют, что в конус вписана правильная двенадцатиугольная пирамида. Первые три грани показаны на чертеже. Разрезают поверхность конуса по образующей S6. Как известно из геометрии, развертка конуса изображается сектором круга, у которого радиус равен длине образующей конуса l. Все образующие кругового конуса равны, поэтому действительная длина образующей l равна фронтальной проекции левой (или правой) образующей. От точки S0 по вертикали откладывают отрезок 5000 =l. Этим радиусом проводят дугу окружности. От точки O0 откладывают отрезки Оl0= O1l1, 1020 = 1121 и т. д. Отложив шесть отрезков, получают точку 60, которую соединяют с вершиной S0. Аналогично строят левую часть развертки; снизу пристраивают основание конуса.
Если требуется нанести на развертку точку В, то проводят через нее образующую SB (в нашем случае S2), наносят эту образующую на развертку (S020); вращая образующую с точкой В вправо до совмещения ее с образующей S3 (S252), находят действительное расстояние S2B2 и откладывают его от точки S0. Найденные отрезки помечены на чертежах тремя штрихами.
Если на развертке конуса не требуется наносить точки, то она может быть построена быстрее и точнее, поскольку известно, что угол сектора развертки a=360°R/l радиус окружности основания, а l — длина образующей конуса.
Если задана поверхность прямого конуса, то развертка его боковой поверхности представляет круговой сектор, радиус которого равен длине образующей конической поверхности l, а центральный угол ц=360о r / l, где r - радиус окружности основания конуса [5 с. 227].
Построение сферы
1) разделить большими окружностями на несколько равных частей. Каждый из образовавшихся элементов сферы проецируется на плоскость П1, в виде сектора;
2) описать вокруг сферы цилиндрическую поверхность, ось которой проходит через центр сферы перпендикулярно к П2;
3) заменить элемент сферы частью цилиндрической поверхности. Горизонтальной проекцией этого цилиндрического элемента окажется треугольник А1В1О1, а фронтальной – контур сферы (дуга окружности) .
4) для построения развертки цилиндрического элемента (лепестка) разделить его фронтальную проекцию на восемь равных частей;
5) построить горизонтальные проекции образующих, соответствующих точкам деления. Истинные длины отрезков образующих для построения развертки взять с горизонтальной проекции (отрезки А1 В1, С1 D1, E1 F1, G1 H1) а расстояния между ними измерить на фронтальной проекции (расстояния между точками 1222, и 2232);
6) при построении цилиндрического элемента (лепестка) через середину отрезка АВ = А1В1 провести вертикальную ось симметрии лепестка на которой отложить вверх и вниз четыре отрезка 10 –20 = 1222, 20 – 30 = 2232, 30 – 40 = 3242, 40 – 50 = 4252.
7) через точки 20, 30, 40 провести отрезки C0D0 = C1D1, E0F0, G0H0 = G1H1.
8) соединить плавной кривой концы отрезков, в результате чего получится развертка верхней половины лепестка [15].
Построение тора
Развертка тора - это приближенное решение задачи по совмещению поверхности тора с плоскостью. Потому что поверхность тора относится к не развертываемым поверхностям.
Для того чтобы построить развертку используем способ вспомогательных цилиндрических поверхностей.
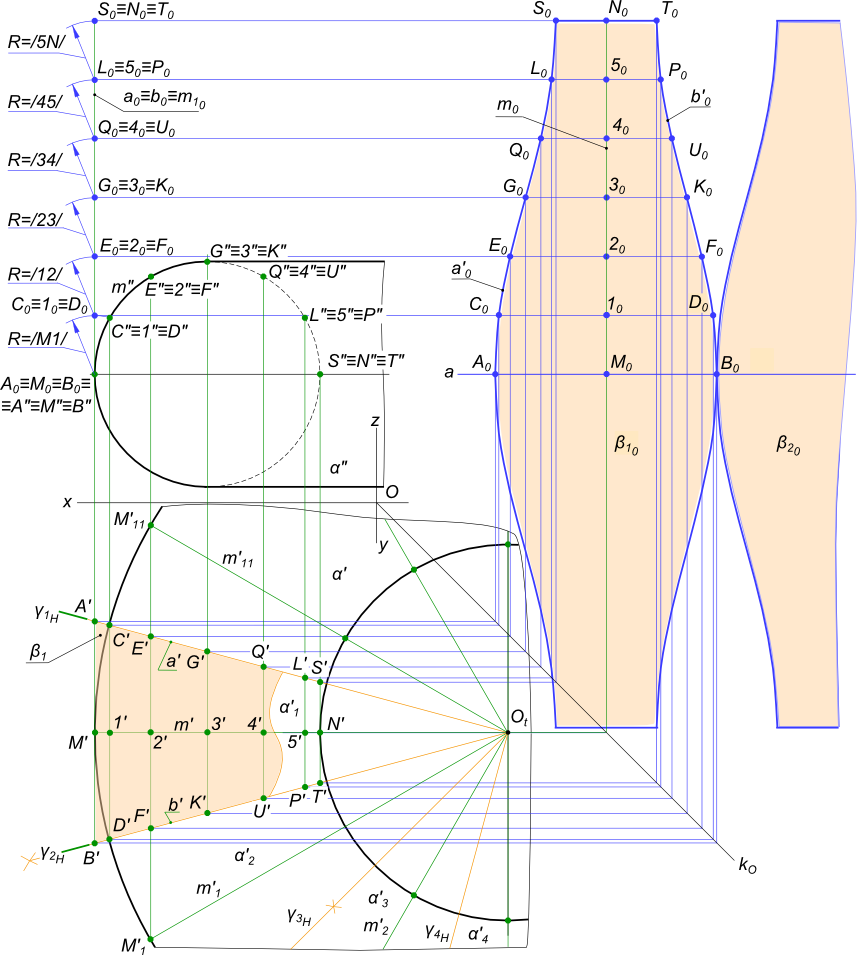
Поверхность тора α делят на какое-либо количество равных частей (в данном случае 12 α1, α2, ..., α12) горизонтально- проецирующими плоскостями γ1, γ2, ...,γ11, проходящими через центр тора. Каждая из них подвергается замене вспомогательной цилиндрической поверхностью β1, β2, ..., β12, которые строятся касательно поверхности тора.
Развертка тора - выполняется на примере (1/12) ее части, как развертка вспомогательной цилиндрической поверхности β1:
- чтобы разделить тор на равные части выполняем деление очерковой окружности α` с помощью циркуля, отмечая точки M`, M`1, ..., M`11 и меридианы m`1, m`2, ..., m`11, проходящие через них;
- две смежных дуги очерковой окружности α` с помощью циркуля делим пополам и проводим γ1H, γ2H;
- делим дугу меридиана m" на двенадцать равных части отмечая точки M", 1", 2", 3", 4", 5", N";
- на горизонтальной проекции строим образующие цилиндрической поверхности β1 проходящие через отмеченные точки M`, 1`, 2`, 3`, 4`, 5`, N` и ограниченные секущими плоскостями в точках A` B`, C` D`, G` K`, Q`U`, L`P`, S`T` соответственно;
- на фронтальной плоскости проекций выполняем развертку меридиана m".
Подготовительные построения закончены, приступаем к построению развертки цилиндрической поверхности β1:
- проводим горизонтальную прямую a проходящую через центр тора;
- в прямоугольной системе координат строим постоянной прямую;
- по линиям связи строим точки развертки и соединив их плавными линиями получаем фигуру A0 S0 T0 B0, которая представляет собой приближенную развертку половины поверхности тора α1;
- пристроив к ней вторую половину симметрично относительно линии a получим развертку β10 соответствующего полной поверхности α1;
- вся развертка тора α может быть получена пристраиванием к β10, одной за другой, 11 фигур равных β10 [17].
Итак, вданном пункте 2 главы мы изучили построение развертки тел вращения. Усвоили, что развертками поверхностей мы часто встречаемся и в обыденной жизни. Освоили алгоритмы и способы построения развертки тел вращения.