Глава 2. Моделирование пространственных тел
Построение разверток многогранников
С развертками поверхностей мы часто встречаемся в обыденной жизни, на производстве и в строительстве. Чтобы изготовить футляр для книги сшить чехол для чемодана, покрышку для волейбольного мяча и т. п., надо уметь строить развертки поверхностей призмы, шара и других геометрических тел [6 с. 4].
При знакомствев школес построением развертки возникает много проблем, у учеников, которые только начинают изучать стереометрию, от неумения сделать правильный и удобный рисунок, или чертеж (развертку). Часто учащиеся не понимают, как пространственные фигуры изобразить на плоскости, правильно оперировать ими, так как чертеж несет в себе смысловую нагрузку, не понятную школьникам. Наглядные и правильно выполненные чертежи, развертки обладают определенной спецификой изображения на них пространственных фигур, и очень важно овладеть этой спецификой, изображать верно, и наглядно пространственные фигуры. Поэтому учитель должен подготовить детей перед знакомством с новой темой построение пространственных фигур. Найти подход к каждому ребенку, так как в классе учатся и не успевающие дети и более сильные [6 с. 4].
Разверткой называется плоская фигура, полученная при совмещении поверхности геометрического тела с одной плоскостью (без наложения граней или иных элементов поверхности друг на друга).Для одних тел развертки могут быть точными, для других — приближенными. Точные развертки имеют все многогранники призмы, пирамиды, цилиндрические и конические поверхности и некоторые другие. Приближенные развертки имеют шар, тор и другие поверхности вращения с криволинейной образующей. Первую группу поверхностей будем называть развертывающимися, вторую — не развёртывающимися [6 с. 4].
При построении разверток многогранников придется находить действительную величину ребер и граней этих многогранников с помощью вращения или перемены плоскостей проекций. При построении приближенных разверток для не развёртывающихся поверхностей придется заменять участки последних близкими к ним по форме развертывающимися поверхностями.
Свойства развертки тел:
1.Длины двух соответствующих линий поверхности и ее развертки равны между собой;
2. Угол между линиями на поверхности равен углу между соответствующими им линиями на развертке;
3. Прямой на поверхности соответствует также прямая на развертке;
4. Параллельным прямым на поверхности соответствуют также параллельные прямые на развертке;
5. Если линии, принадлежащей поверхности и соединяющей две точки поверхности, соответствует прямая на развертке, то эта линия является геодезической.
Существует три способа построения развертки многогранных поверхностей:
1. Способ нормального сечения;
2. Способ раскатки;
3. Способ треугольника. [6 с. 4-5]
Пирамида и её развертка
При построении развертки пирамида применяется способ треугольника. Развертка боковой поверхности пирамиды представляет собой плоскую фигуру, состоящую из треугольников - граней пирамиды и многоугольника - основания. Поэтому построение развертки пирамиды сводится к определению натуральной величины основания и граней пирамиды. Грани пирамиды можно построить по трем сторонам треугольников, их образующих. Для этого необходимо знать натуральную величину ребер и сторон основания. 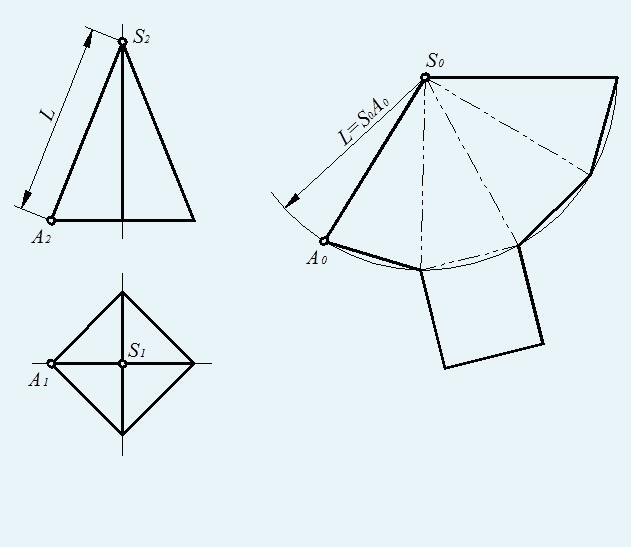
Ученикам в школе следует показать и объяснить алгоритм построения пирамиды. Так как могут возникнуть затруднения в понимании.
1. Определяют натуральную величину основания пирамиды (например методом замены плоскостей проекций);
2. Определяют истинную величину всех ребер пирамиды любым из известных способов (в данном примере натуральная величина всех ребер пирамиды определена методом вращения вокруг оси перпендикулярной горизонтальной плоскости проекций и проходящей через вершину пирамиды S);
3. Строят основание пирамиды и по найденным трем сторонам строят какую-либо из боковых граней, пристраивая к ней следующие.
Точки, расположенные внутри контура развертки, находят во взаимно однозначном соответствии с точками поверхности многогранника. Но каждой точке тех ребер, по которым многогранник разрезан, на развертке соответствуют две точки, принадлежащие контуру развертки [16].
 Построение призмы
Построение призмы
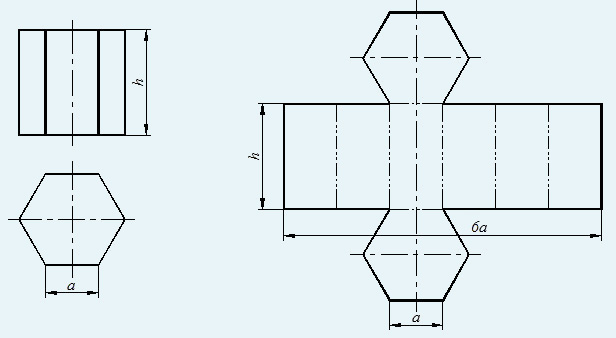
В общем случае развертка призмы выполняется следующим образом. Преобразуют чертеж так, чтобы ребра призмы стали параллельны новой плоскости проекций. Тогда на эту плоскость ребра проецируются в натуральную величину.Пересекая призму вспомогательной плоскостью б, перпендикулярной ее боковым ребрам (способ нормального сечения), строят проекции фигуры нормального сечения - треугольника 1, 2, 3, а затем определяют истинную величину этого сечения.В дальнейшем строям отрезок 10-10*, равный периметру нормального сечения. Через точки 10, 20, 30 и 10* проводят прямые, перпендикулярные 10-10*, на которых откладывают соответствующие отрезки боковых ребер призмы, беря их с новой фронтальной проекции. Так, на перпендикуляре, проходящем через точку 10, отложены отрезки 10D0=14D4 и 10А0=14А4.
Соединив концы отложенных отрезков, получают развертку боковой поверхности призмы. Затем достраивают основание (рис.4.)[5 с. 10].
Развертка боковой поверхности такой призмы осуществляется способом раскатки. Этот способ заключается в следующем. Сначала, как и в предыдущем примере, преобразуют эпюр так, чтобы боковые ребра призмы стали параллельны одной из плоскостей проекций.
Затем новую проекцию призмы вращают вокруг ребра С4F4 до тех пор пока грань ACDF не станет параллельной плоскости П4. При этом положение ребра С4F4 остается неизменным, а точки принадлежащие ребру AD перемещаются по окружностям, радиус которых определяется натуральной величиной отрезков AC и DF (так как основания призмы параллельны П1 то на эту плоскость проекций они проецируются без искажения т.е. R=A1C1=D1F1), расположенных в плоскостях, перпендикулярных ребру С4F4. Таким образом, траектории движения точек A и D на плоскость П4 проецируются в прямые, перпендикулярные ребру С4F4.
Когда грань ACDF станет параллельна плоскости П4, она проецируется на неё без искажения т.е. вершины A и D окажутся удаленными от неподвижных вершин C и F на расстояние, равное натуральной величине отрезков AC и DF. Таким образом, засекая перпендикуляры, по которым перемещаются точки A4 и D4 дугой радиуса R=A1C1=D1F1, можно получить искомое положение точек развертки A0 и D0.
Следующую грань АBDE вращают вокруг ребра AD. На перпендикулярах, по которым перемещаются точки B4 и E4 делают засечки из точек A0 и D0 дугой радиуса R=A1B1=D1E1. Аналогично строится развертка последней боковой грани призмы.
Процесс последовательного нахождения граней призмы вращением вокруг ребер можно представить как раскатку призмы на плоскость параллельную П4 и проходящую через ребро С4F4.
Построение на развертке точки К, принадлежащей боковой грани АBDE, ясно из рисунка. Предварительно через эту точку по грани провели прямую NМ, параллельную боковым ребрам, которая затем построена на развертке [5 с. 10].
 Построение куба
Построение куба
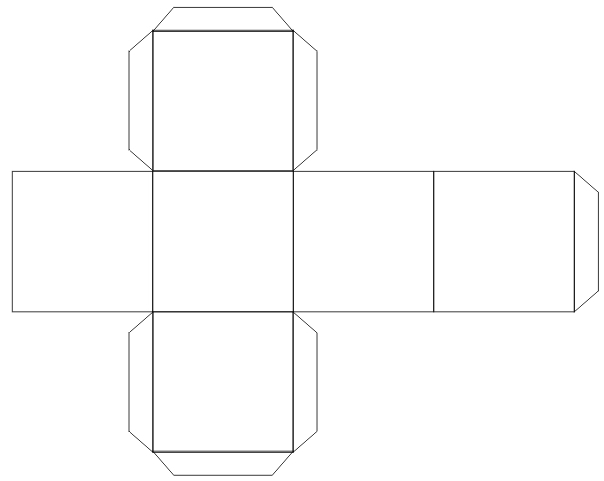
Развертку куба строим по следующему алгоритму.
1. Чертим окружность с центром О и радиусом ОС, назовем ее исходной.
2. Строим прямую проходящую через центр окружности точку О.
3. Отмечаем точки D и C, в местах пересечения прямой и окружности.
4. Строим две окружности, первую с центром D и радиусом DC, вторую с центром С и тем же радиусом DC.
5. Отмечаем точи пересечения построенных окружностей А и В.
6. Строим прямую АВ. Если построение аккуратное, то она (прямая АВ) должна пройти через точу О и будет перпендикулярной отрезку DC.
7. Отмечаем точки F и G, как пересечения прямой АВ и нашей исходной окружности.
8. Соединяем точки C,F,D,G, имеем квадрат, первую грань куба.
9. Строим две окружности с центрами в точках C и F и радиусами равными радиусу исходной окружности, стало быть ОС.
10. Отмечаем точку R, в месте их пересечения.
11. Строим окружность с центром в точке R и тем же радиусом ОС.
12. Продолжаем прямые DF и GC до пересечения с окружностью, с центром R.
13. Отмечаем точки L и K, как точки соответствующих пересечений.
14. Соединяем точки L и K, имеем вторую грань куба — квадрат FLKC.
15. Используя тот же алгоритм, строим остальные грани.
16. Строим окружность с центром G и радиусом равными радиусу исходной окружности.
17. Отмечаем точку M, в месте пересечения окружностей с центрами в точках C и G .
18. Строим окр. с центром в точке M и радиусом ОС.
19. Продолжаем прямые FC и DG до пересечения с окружностью, с центром M.
20. Отмечаем точки N и P, как точки соответствующих пересечений.
21. Соединяем точки N и P, имеем третью грань куба — квадрат GCNP.
22. Строим окружность с центром D и радиусом равными радиусу исходной окружности.
23. Отмечаем точку I, в месте пересечения окружностей с центрами в точках D и G.
24. Строим окр. с центром в точке I и радиусом ОС.
25. Продолжаем прямые FD и CG до пересечения с окружностью, с центром I.
26. Отмечаем точки T и S, как точки соответствующих пересечений.
27. Соединяем точки T и S, имеем четвертую грань куба — квадрат TSDG.
28. Отмечаем точку U, в месте пересечения окружностей с центрами D и F
29. Строим окр. с центром в точке U и радиусом ОС.
30. Продолжаем прямые DG и CF до пересечения с окружностью, с центром U.
31. Отмечаем точки H и Q, как точки соответствующих пересечений.
32. Соединяем точки H и Q, имеем пятую грань куба — квадрат HQDF.
33. Строим окружности с центрами N , P и радиусами равными радиусу исходной окружности.
34. Отмечаем точку Х, в месте пересечения окружностей с центрами в точках N , P.
35. Строим окр. с центром в точке Х и радиусом ОС.
36. Продолжаем прямые HP и QN до пересечения с окружностью, с центром X.
37. Отмечаем точки Y и Z, как точки соответствующих пересечений.
38. Соединяем точки Y и Z, имеем шестую грань куба.
39. Построение закончено [20].
 Построение развертки параллелепипеда
Построение развертки параллелепипеда
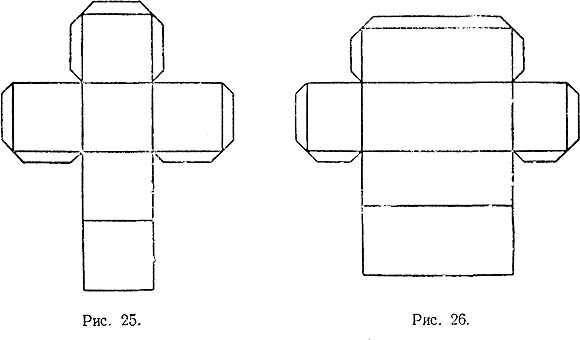
Алгоритм построения:
1)Построить прямоугольник заданной длины (а) и высоты (h).
2)Из каждой вершины отложить отрезок, равный половине ширины (в) под углом 45 градусов.
3)Соединить концы отрезков, причем невидимые грани – пунктирной линией [16].
Таким образом, в данном пункте мыосвоили построение развертки многогранников. Познакомились с понятием развертки, свойствами и способами построения. Изучили алгоритмы построения многогранников.
