Глава 1 Теоретические сведения о пространственных телах

Оглавление

Стр.

Введение
Глава 1. Теоретические сведения о пространственных телах
1.1. Понятие и свойства многогранников
1.2. Понятие и свойства тел вращения
Глава 2. Моделирование пространственных тел
2.1. Построение разверток многогранников
2.2. Построение разверток тел вращения
2.3. Моделирование пространственных тел в начальной школе
Заключение
Список литературы

Введение

Человек проявляет интерес к пространственным телам на протяжении всей своей жизни - от двухлетнего возраста, когда ребенок играет деревянными кубиками, до зрелого математика. Потому что человек сталкивается в своей деятельности повсюду с необходимостью изучать их форму, размеры, взаимное расположение пространственных фигур. Подобные задачи решают и астрономы, имеющие дело с самыми большими масштабами, и физики, исследующие структуру атомов и молекул. Особый интерес к пространственным телам связан с красотой и совершенством формы. Они довольно часто встречаются в природе. Достаточно вспомнить форму снежинок, граней кристаллов, ячеек в пчелиных сотах [14].

Актуальность данного исследования состоит в том, что пространственные тела – «вечные» тела. Интерес к ним тонкой нитью проходит через спираль всех времен. Чем же обусловлен столь бессмертный интерес? Например, считается, что в основе строения Платоновых тел заложены пропорции всего, из чего состоит мир. Поэтому эти уникальные фигуры и получили название «ключи мироздания». Так же, формы пространственных тел находят широкое применение в конструировании сложных многогранных поверхностей, которые используются в реальных архитектурных проектах [14].

Эту тему я выбрала потому, что изучение пространственных тел является одним из центральных в курсе стереометрии. Но способность же учащихся мысленно представлять себе фигуры их положения в пространстве нужно развивать задолго до того, как приходит пора изучать стереометрию.Это можно объяснить тем, что учителя математики часто недооценивают возможностей применение моделей, хотя они могут существенно повысить эффективность усвоения материала, а также служить развитию и поддержанию интереса к предмету.

«Прошли века, но роль геометрии не изменилась. Она по-прежнему остаётся грамматикой архитектора» - это высказывание принадлежит великому французскому архитектору Ле Корбюзье. (1887-1965). Я ничуть не сомневаюсь в его словах. Поэтому мне захотелось больше узнать о пространственных телах.

Пространственные тела изучались еще с древних времен. Одними из первых ученых были Платон, Евклид, Архимед. В эпоху Возрождения ученые изучали и дальше развивали их учения [11 с. 144].

Исходя из актуальности рассматриваемого вопроса, мной выбрана тема исследования: «Моделирование пространственных тел».

Объект: пространственные тела

Предмет: моделирование пространственных тел.

Цель: выявления закономерностей структуры пространственных тел, изучение заданных характеристик тел.

Задачи:

1) Рассмотреть понятия многогранника и его свойства

2) Изучить тела вращения и их свойства

3) Освоить построение развертки многогранника

4) Изучить построение тел вращения

5) Ознакомиться с моделированием пространственных тел в начальной школе

Глава 1 Теоретические сведения о пространственных телах

Глава 2. Моделирование пространственных тел

Пирамида и её развертка

При построении развертки пирамида применяется способ треугольника. Развертка боковой поверхности пирамиды представляет собой плоскую фигуру, состоящую из треугольников - граней пирамиды и многоугольника - основания. Поэтому построение развертки пирамиды сводится к определению натуральной величины основания и граней пирамиды. Грани пирамиды можно построить по трем сторонам треугольников, их образующих. Для этого необходимо знать натуральную величину ребер и сторон основания. 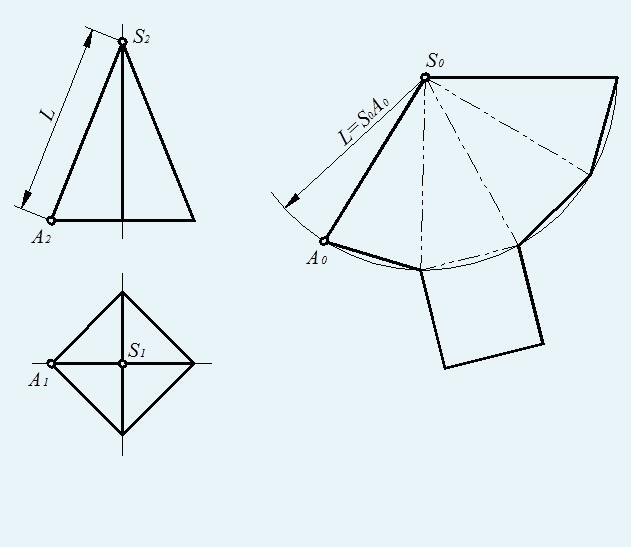Глава 1 Теоретические сведения о пространственных телах - student2.ru

Ученикам в школе следует показать и объяснить алгоритм построения пирамиды. Так как могут возникнуть затруднения в понимании.

1. Определяют натуральную величину основания пирамиды (например методом замены плоскостей проекций);

2. Определяют истинную величину всех ребер пирамиды любым из известных способов (в данном примере натуральная величина всех ребер пирамиды определена методом вращения вокруг оси перпендикулярной горизонтальной плоскости проекций и проходящей через вершину пирамиды S);

3. Строят основание пирамиды и по найденным трем сторонам строят какую-либо из боковых граней, пристраивая к ней следующие.

Точки, расположенные внутри контура развертки, находят во взаимно однозначном соответствии с точками поверхности многогранника. Но каждой точке тех ребер, по которым многогранник разрезан, на развертке соответствуют две точки, принадлежащие контуру развертки [16].

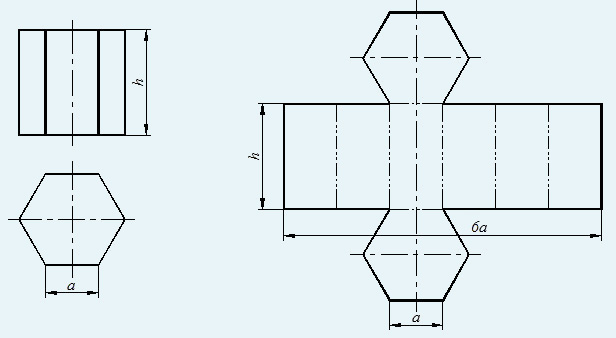Глава 1 Теоретические сведения о пространственных телах - student2.ru Построение призмы

В общем случае развертка призмы выполняется следующим образом. Преобразуют чертеж так, чтобы ребра призмы стали параллельны новой плоскости проекций. Тогда на эту плоскость ребра проецируются в натуральную величину.Пересекая призму вспомогательной плоскостью б, перпендикулярной ее боковым ребрам (способ нормального сечения), строят проекции фигуры нормального сечения - треугольника 1, 2, 3, а затем определяют истинную величину этого сечения.В дальнейшем строям отрезок 10-10*, равный периметру нормального сечения. Через точки 10, 20, 30 и 10* проводят прямые, перпендикулярные 10-10*, на которых откладывают соответствующие отрезки боковых ребер призмы, беря их с новой фронтальной проекции. Так, на перпендикуляре, проходящем через точку 10, отложены отрезки 10D0=14D4 и 10А0=14А4.

Соединив концы отложенных отрезков, получают развертку боковой поверхности призмы. Затем достраивают основание (рис.4.)[5 с. 10].

Развертка боковой поверхности такой призмы осуществляется способом раскатки. Этот способ заключается в следующем. Сначала, как и в предыдущем примере, преобразуют эпюр так, чтобы боковые ребра призмы стали параллельны одной из плоскостей проекций.

Затем новую проекцию призмы вращают вокруг ребра С4F4 до тех пор пока грань ACDF не станет параллельной плоскости П4. При этом положение ребра С4F4 остается неизменным, а точки принадлежащие ребру AD перемещаются по окружностям, радиус которых определяется натуральной величиной отрезков AC и DF (так как основания призмы параллельны П1 то на эту плоскость проекций они проецируются без искажения т.е. R=A1C1=D1F1), расположенных в плоскостях, перпендикулярных ребру С4F4. Таким образом, траектории движения точек A и D на плоскость П4 проецируются в прямые, перпендикулярные ребру С4F4.

Когда грань ACDF станет параллельна плоскости П4, она проецируется на неё без искажения т.е. вершины A и D окажутся удаленными от неподвижных вершин C и F на расстояние, равное натуральной величине отрезков AC и DF. Таким образом, засекая перпендикуляры, по которым перемещаются точки A4 и D4 дугой радиуса R=A1C1=D1F1, можно получить искомое положение точек развертки A0 и D0.

Следующую грань АBDE вращают вокруг ребра AD. На перпендикулярах, по которым перемещаются точки B4 и E4 делают засечки из точек A0 и D0 дугой радиуса R=A1B1=D1E1. Аналогично строится развертка последней боковой грани призмы.

Процесс последовательного нахождения граней призмы вращением вокруг ребер можно представить как раскатку призмы на плоскость параллельную П4 и проходящую через ребро С4F4.

Построение на развертке точки К, принадлежащей боковой грани АBDE, ясно из рисунка. Предварительно через эту точку по грани провели прямую NМ, параллельную боковым ребрам, которая затем построена на развертке [5 с. 10].

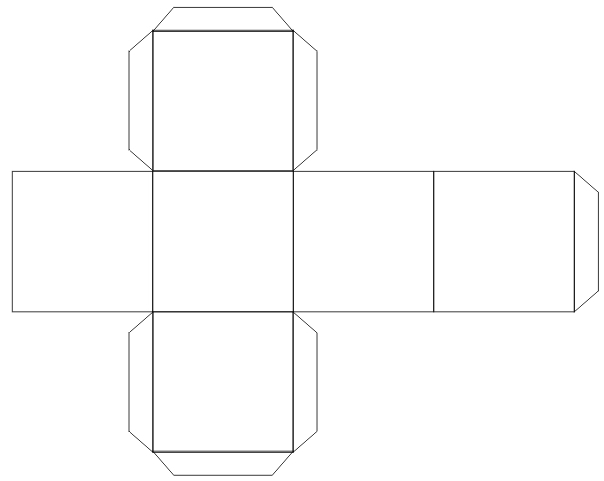Глава 1 Теоретические сведения о пространственных телах - student2.ru Построение куба

Развертку куба строим по следующему алгоритму.

1. Чертим окружность с центром О и радиусом ОС, назовем ее исходной.

2. Строим прямую проходящую через центр окружности точку О.

3. Отмечаем точки D и C, в местах пересечения прямой и окружности.

4. Строим две окружности, первую с центром D и радиусом DC, вторую с центром С и тем же радиусом DC.

5. Отмечаем точи пересечения построенных окружностей А и В.

6. Строим прямую АВ. Если построение аккуратное, то она (прямая АВ) должна пройти через точу О и будет перпендикулярной отрезку DC.

7. Отмечаем точки F и G, как пересечения прямой АВ и нашей исходной окружности.

8. Соединяем точки C,F,D,G, имеем квадрат, первую грань куба.

9. Строим две окружности с центрами в точках C и F и радиусами равными радиусу исходной окружности, стало быть ОС.

10. Отмечаем точку R, в месте их пересечения.

11. Строим окружность с центром в точке R и тем же радиусом ОС.

12. Продолжаем прямые DF и GC до пересечения с окружностью, с центром R.

13. Отмечаем точки L и K, как точки соответствующих пересечений.

14. Соединяем точки L и K, имеем вторую грань куба — квадрат FLKC.

15. Используя тот же алгоритм, строим остальные грани.

16. Строим окружность с центром G и радиусом равными радиусу исходной окружности.

17. Отмечаем точку M, в месте пересечения окружностей с центрами в точках C и G .

18. Строим окр. с центром в точке M и радиусом ОС.

19. Продолжаем прямые FC и DG до пересечения с окружностью, с центром M.

20. Отмечаем точки N и P, как точки соответствующих пересечений.

21. Соединяем точки N и P, имеем третью грань куба — квадрат GCNP.

22. Строим окружность с центром D и радиусом равными радиусу исходной окружности.

23. Отмечаем точку I, в месте пересечения окружностей с центрами в точках D и G.

24. Строим окр. с центром в точке I и радиусом ОС.

25. Продолжаем прямые FD и CG до пересечения с окружностью, с центром I.

26. Отмечаем точки T и S, как точки соответствующих пересечений.

27. Соединяем точки T и S, имеем четвертую грань куба — квадрат TSDG.

28. Отмечаем точку U, в месте пересечения окружностей с центрами D и F

29. Строим окр. с центром в точке U и радиусом ОС.

30. Продолжаем прямые DG и CF до пересечения с окружностью, с центром U.

31. Отмечаем точки H и Q, как точки соответствующих пересечений.

32. Соединяем точки H и Q, имеем пятую грань куба — квадрат HQDF.

33. Строим окружности с центрами N , P и радиусами равными радиусу исходной окружности.

34. Отмечаем точку Х, в месте пересечения окружностей с центрами в точках N , P.

35. Строим окр. с центром в точке Х и радиусом ОС.

36. Продолжаем прямые HP и QN до пересечения с окружностью, с центром X.

37. Отмечаем точки Y и Z, как точки соответствующих пересечений.

38. Соединяем точки Y и Z, имеем шестую грань куба.

39. Построение закончено [20].

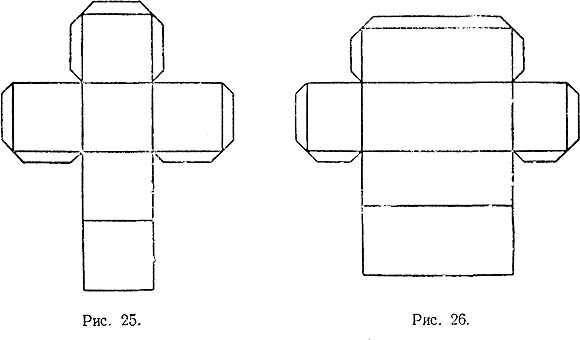Глава 1 Теоретические сведения о пространственных телах - student2.ru Построение развертки параллелепипеда

Алгоритм построения:

1)Построить прямоугольник заданной длины (а) и высоты (h).

2)Из каждой вершины отложить отрезок, равный половине ширины (в) под углом 45 градусов.

3)Соединить концы отрезков, причем невидимые грани – пунктирной линией [16].

Таким образом, в данном пункте мыосвоили построение развертки многогранников. Познакомились с понятием развертки, свойствами и способами построения. Изучили алгоритмы построения многогранников.

Построение сферы

1) разделить большими окружностями на несколько равных частей. Каждый из образовавшихся элементов сферы проецируется на плоскость П1, в виде сектора;

2) описать вокруг сферы цилиндрическую поверхность, ось которой проходит через центр сферы перпендикулярно к П2;

3) заменить элемент сферы частью цилиндрической поверхности. Горизонтальной проекцией этого цилиндрического элемента окажется треугольник А1В1О1, а фронтальной – контур сферы (дуга окружности) .

4) для построения развертки цилиндрического элемента (лепестка) разделить его фронтальную проекцию на восемь равных частей;

5) построить горизонтальные проекции образующих, соответствующих точкам деления. Истинные длины отрезков образующих для построения развертки взять с горизонтальной проекции (отрезки А1 В1, С1 D1, E1 F1, G1 H1) а расстояния между ними измерить на фронтальной проекции (расстояния между точками 1222, и 2232);

6) при построении цилиндрического элемента (лепестка) через середину отрезка АВ = А1В1 провести вертикальную ось симметрии лепестка на которой отложить вверх и вниз четыре отрезка 10 –20 = 1222, 20 – 30 = 2232, 30 – 40 = 3242, 40 – 50 = 4252.

7) через точки 20, 30, 40 провести отрезки C0D0 = C1D1, E0F0, G0H0 = G1H1.

8) соединить плавной кривой концы отрезков, в результате чего получится развертка верхней половины лепестка [15].

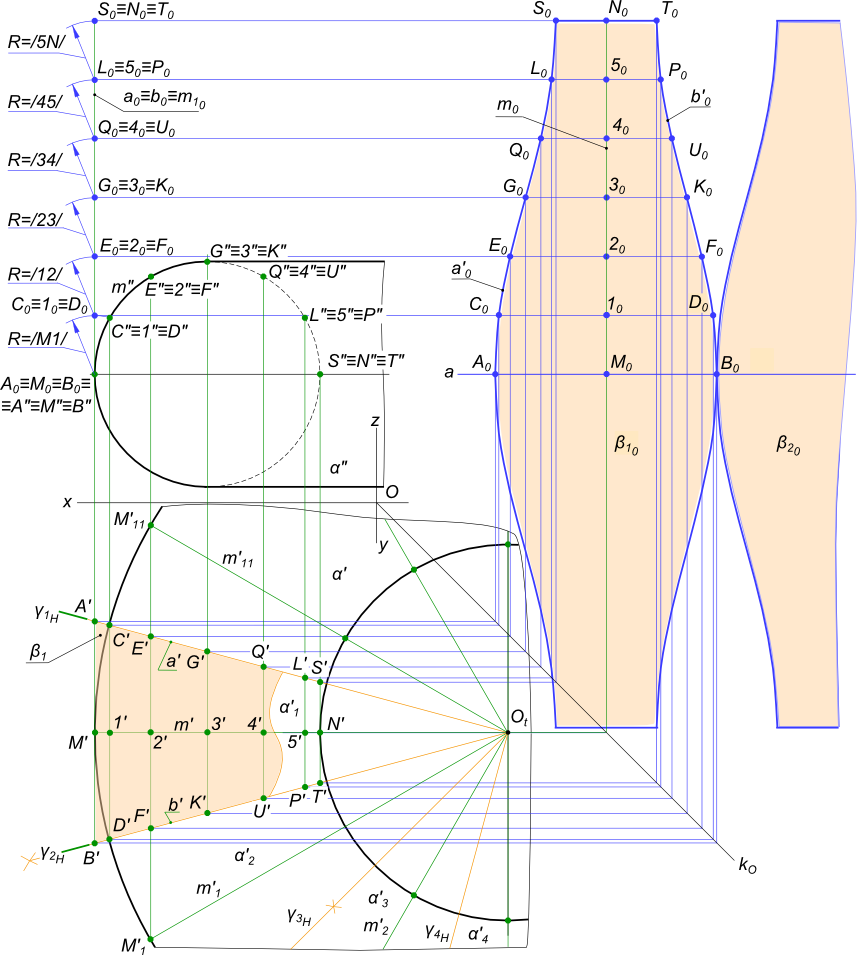Глава 1 Теоретические сведения о пространственных телах - student2.ru Построение тора

Развертка тора - это приближенное решение задачи по совмещению поверхности тора с плоскостью. Потому что поверхность тора относится к не развертываемым поверхностям.

Для того чтобы построить развертку используем способ вспомогательных цилиндрических поверхностей.

Поверхность тора α делят на какое-либо количество равных частей (в данном случае 12 α1, α2, ..., α12) горизонтально- проецирующими плоскостями γ1, γ2, ...,γ11, проходящими через центр тора. Каждая из них подвергается замене вспомогательной цилиндрической поверхностью β1, β2, ..., β12, которые строятся касательно поверхности тора.

Развертка тора - выполняется на примере (1/12) ее части, как развертка вспомогательной цилиндрической поверхности β1:

- чтобы разделить тор на равные части выполняем деление очерковой окружности α` с помощью циркуля, отмечая точки M`, M`1, ..., M`11 и меридианы m`1, m`2, ..., m`11, проходящие через них;

- две смежных дуги очерковой окружности α` с помощью циркуля делим пополам и проводим γ1H, γ2H;

- делим дугу меридиана m" на двенадцать равных части отмечая точки M", 1", 2", 3", 4", 5", N";

- на горизонтальной проекции строим образующие цилиндрической поверхности β1 проходящие через отмеченные точки M`, 1`, 2`, 3`, 4`, 5`, N` и ограниченные секущими плоскостями в точках A` B`, C` D`, G` K`, Q`U`, L`P`, S`T` соответственно;

- на фронтальной плоскости проекций выполняем развертку меридиана m".

Подготовительные построения закончены, приступаем к построению развертки цилиндрической поверхности β1:

- проводим горизонтальную прямую a проходящую через центр тора;

- в прямоугольной системе координат строим постоянной прямую;

- по линиям связи строим точки развертки и соединив их плавными линиями получаем фигуру A0 S0 T0 B0, которая представляет собой приближенную развертку половины поверхности тора α1;

- пристроив к ней вторую половину симметрично относительно линии a получим развертку β10 соответствующего полной поверхности α1;

- вся развертка тора α может быть получена пристраиванием к β10, одной за другой, 11 фигур равных β10 [17].

Итак, вданном пункте 2 главы мы изучили построение развертки тел вращения. Усвоили, что развертками поверхностей мы часто встречаемся и в обыденной жизни. Освоили алгоритмы и способы построения развертки тел вращения.

Заключение

Целью данной работы было выявления закономерностей структуры пространственных тел, изучение заданных характеристик тел. Было доказано, что пространственные тела – «вечные» тела. Они нас окружают повсеместно в нашей деятельности.

В работе ставились и были решены следующие задачи:

1)Рассмотрели понятия многогранника и его свойства. Перечислили виды многогранника. Ознакомились с историей открытия многогранника. Установили, что многогранники имеют большое значение в природе и для человека. Так, например, многогранники применяются в конструировании.

2)Были изучены тела вращения и их свойства. Описали понятие тел вращения. Привели примеры. Проследили и пришли к выводу, что дети знакомятся с телами вращения уже в 1 классе начальной школы.

3)Освоили построение развертки многогранников. Познакомились с понятием развертки, свойствами и способами построения. Изучили алгоритмы построения многогранников.

4) Изучили построение развертки тел вращения. Усвоили, что развертками поверхностей мы часто встречаемся и в обыденной жизни.Освоили алгоритмы и способы построения развертки тел вращения.

5)Ознакомились с моделированием тел в начальной школе. Привели примеры разнообразных упражнений из учебников по математике авторов Истоминой, Чекиным, Дорофеевым и др.

Таким образом, цель исследования достигнута.

Список литературы

1) Атанасян Л.С.Геометрия. 10-11 классы: учеб.для общеобразоват. учреждений: базовый и профил. уровни/[ Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др.]. – 22-е изд.— Москва: Просвещение, 2013.— 255 с.

2)Большая энциклопедия Кирилла и Мефодия (http://megabook.ru/article/%D0%A2%D0%BE%D1%80%20(%D0%B2%20%D0%B3%D0%B5%D0%BE%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D0%B8)

3)Виды многогранников (http://www.propro.ru/graphbook/graphbook/book/001/027.htm)

4)Волкова С.И.Альбом по математике и конструированию 2 и 3 класс /С.И. Волкова, О.Л.Пчелкина. – Москва: Просвещение, 2004.— 64 с.

5) Гордон В.О. Семенцов – Огиевский М.А. Курс начертательной геометрии: Учеб. пособие / Под ред.Ю.Б.Иванова. – 23 изд., перераб. – Москва: Наука Гл. ред. Физ. - мат. лит. 1988. – 272 с.

6) ГригорьеваО.О.Развертки поверхностей. Учебно-методические указания/О.О. Григорьева. – Ижевск: Издательство ИжГТУ, 2012. – 25 с.

7) Демидова Т.Е. Математика. 2 кл. : учеб.для организаций, осуществляющих образовательную деятельность. В 3 ч. / Т.Е. Демидова, С.А. Козлова, А.П. Тонких. – Изд. 3-е, испр. – Москва: Баласс, 2016. – 80 с.

8)Дорофеев Г.В. Математика 2 класс Учеб.для общеобразоват. организаций в 2 ч. / Г.В. Дорофеев, Т.Н. Миракова, Т.Б. Бука. – 7-е из. – Москва: Просвещение, 2015. – 122 с.

9)Истомина Н.Б. Математика: учебник для 2 класса общеобразовательных учреждений. В 2 ч. / Н.Б. Истомина. – 13-е изд. – Смоленск: Ассоциация 21 век, 2013. – 120 с.

10)Киселев А. П. Геометрия / Под ред. Н.А. Глаголева. — Москва:

ФИЗМАТЛИТ, 2004. - 328 с.

11)Корниенко Т.Л. Геометрия 11 класс. Академический уровень: Разработки уроков/Т.Л. Корниенко, В.И.Филотина. – Харьков: Издательство «Ранок», 2012. – 304 с.

12)Королев Ю.И. Начертательная геометрия: учебник для вузов / Ю.И. Королев. 2-е изд. – Санкт-Петербург: Питер, 2009г. – 256 с.

13)Многогранник (http://math4school.ru/mnogogranniki.html)

14) Правильный многогранник (http://www.hintfox.com/article/pravilnie-mnogogranniki-v-nayke-i-povsednevnoj-zhizni.html)

15) Построение сферы (https://otvet.mail.ru/question/61375233)

16)Построение разверток поверхностей геометрических тел (http://polynsky.com.kg/proecirovanie/153-postroenie-razvertok-poverkhnostejj.html)

17)Построение тора (https://ngeo.fxyz.ru/%D1%80%D0%B0%D0%B7%D0%B2%D0%B5%D1%80%D1%82%D0%BA%D0%B0_%D0%BF%D0%BE%D0%B2%D0%B5%D1%80%D1%85%D0%BD%D0%BE%D1%81%D1%82%D0%B5%D0%B9/%D0%BD%D0%B5%D1%80%D0%B0%D0%B7%D0%B2%D0%B5%D1%80%D1%82%D1%8B%D0%B2%D0%B5%D0%BC%D1%8B%D0%B5_%D0%BF%D0%BE%D0%B2%D0%B5%D1%80%D1%85%D0%BD%D0%BE%D1%81%D1%82%D0%B8/%D1%80%D0%B0%D0%B7%D0%B2%D0%B5%D1%80%D1%82%D0%BA%D0%B0_%D1%82%D0%BE%D1%80%D0%B0/)

18)Смирнова И.М. Геометрия 10-11. Учебник для общеобразовательных учреждений/И.М. Смирнова, В.А. Смирнов. – Москва: Мнемозина, 2003. —288 с.

19)Стереометрия(http://geometry-and-art.ru/stereo.html)

20)Развертка куба(http://tetraksis.com/1/razvertka-kuba-tsirkulem-i-lineykoy)

21)Рудницкая В.Н. Математика: 1 класс: учебник для учащихся общеобразовательных учреждений: в 2 ч. / В.Н. Рудницкая, Е.Э. Кочурова, О.А. Рыдзе. – 4-е изд., перераб. – Москва: Вентана-Граф, 2011. – 128 с.

22)Что такое многогранник (http://www.mnogogranniki.ru/stati/2-mnogogrannik.html)

23)Чекин А.Л. Математика: 4 класс: Учебник в 2 ч. / А.Л. Чекин; под ред. Р.Г. Чураковой. – 2-е изд. – Москва: Академкнига/Учебник, 2012. -128 с.

Оглавление

Стр.

Введение
Глава 1. Теоретические сведения о пространственных телах
1.1. Понятие и свойства многогранников
1.2. Понятие и свойства тел вращения
Глава 2. Моделирование пространственных тел
2.1. Построение разверток многогранников
2.2. Построение разверток тел вращения
2.3. Моделирование пространственных тел в начальной школе
Заключение
Список литературы