Тема 2.3. Системы 2-х и 3-х линейных уравнений с действительными коэффициентами.
Практическая работа № 10
Решение систем линейных алгебраических уравнений с действительными коэффициентами.
«Решение систем линейных уравнений методом Крамера»
Цель работы:научиться решать системы линейных уравнений методом Крамера.
Образовательные результаты, заявленные во ФГОС:
Студент должен
уметь:
- решать системы линейных уравнений.
знать:
- основы математического анализа, линейной алгебры и аналитической геометрии.
Оборудование: рабочая тетрадь, ручка, методические рекомендации по выполнению практической работы, справочная литература.
Методические указания по выполнению работы:
1. Ознакомиться с теоретическим материалом по практической работе.
2. Рассмотрите образцы решения задач по теме.
3.Выполнить предложенное задание согласно варианту по списку группы.
4.Изучить условие заданий для практической работы и выполнить её.
5. Ответить на контрольные вопросы даются письменно, после решения заданий в тетради для практических работ. Во время выполнения работы обучающийся может пользоваться своим конспектом, а также учебной литературой и справочным материалом.
5. Оформить отчет о работе. Сделайте вывод.
Краткие теоретические и учебно-методические материалы по теме практической работы
Метод Крамера решения систем линейных уравнений
Матричное равенство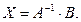 
запишем в виде:
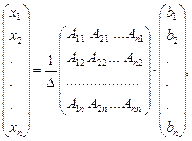(7)
или
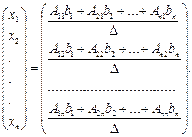(8)
Отсюда следует, что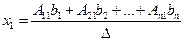 
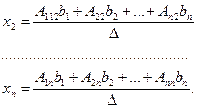(9)
Но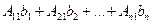 
есть разложение определителя
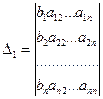
по элементам первого столбца. Определитель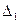 
получается из определителя 
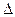путем замены первого столбца коэффициентов столбцом свободных членов. Итак, 
.
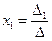Аналогично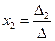 
, где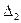 
получен из 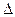путем замены второго столбца коэффициентов столбцом свободных членов, 
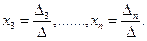Формулы
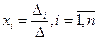(10)
называются формулами Крамера.
Пример по выполнению практической работы
Пример 1. Решить систему методом Крамера:
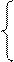3x1 + x2 – 2x3 = 6;
5x1 – 3x2 + 2x3 = -4;
4x1 – 2x2 – 3x3 = -2.
Находим главный определитель системы:
 |
3 1 -2
∆ = 5 -3 2 = 3∙(-3) ∙ (-3) + 1∙ 2∙ 4 + 5∙(-2) ∙ (-2) – 4∙(-3) ∙ (-2) – 5∙ 1∙(-3) –
4 -2 -3 - (-2) ∙ 2∙ 3 =27 +8 +20 -24 + 15 + 12 = 58.
Так как главный определитель системы не равен нулю, то она совместна. Находим определители: ∆x1, ∆x2, ∆x3. Определитель ∆x1 получается из главного определителя ∆ путём замены в нём первого столбца на столбец свободных членов.
 | |
6 1 -2
∆x1 = -4 -3 2 = 54 – 4 – 16 + 12 – 12 + 24 = 58.
-2 -2 -3
Т.к. ∆x1 отличен от нуля, значит решение системы единственное. Определитель ∆x2 получается из главного определителя ∆ путём замены в нём второго столбца на столбец свободных членов.
3 6 -2
∆x2 = 5 -4 2 = 36 + 48 + 20 – 32 + 90 + 12 = 174.
4 -2 -3
Определитель ∆x3 получается из главного определителя ∆ путём замены в нём третьего столбца на столбец свободных членов.
| | |
3 1 6
∆x3 = 5 -3 -4 = 18 – 16 – 60 + 72 + 10 – 24 = 0.
4 -2 -2
По формулам Крамера: x1 = =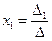 
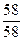=1; x2 = = 
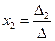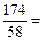3 ; 
= 
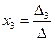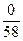= 0.
Итак, решением системы будет тройка чисел (1; 3; 0).
Задания для практического занятия:
Вариант 1
1. Решить систему методом Крамера:
а)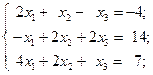 
б) 
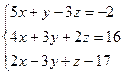в)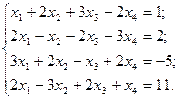 
Вариант 2
1. Решить систему методом Крамера:
а)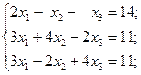 
б) 
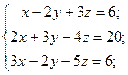в)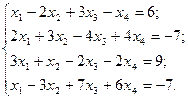 
Вариант 3
1. Решить систему методом Крамера:
а)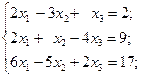 
б) 
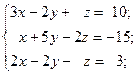в)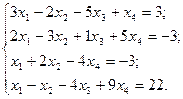 
Вариант 4
1. Решить систему методом Крамера:
а)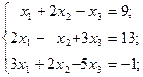 
б) 
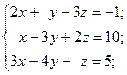в)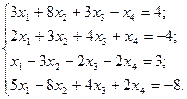 
Контрольные вопросы
1. В каком случае система уравнений будет несовместной при решении методом Крамера;
2. Напишите общий вид формул Крамера;
3. Опишите метод Крамера решения систем линейных уравнений.
Практическая работа № 11-12
Решение систем линейных алгебраических уравнений с действительными коэффициентами.
«Решение систем линейных уравнений методом Гаусса»
Цель работы:научиться решать системы линейных уравнений методом Гаусса.
Образовательные результаты, заявленные во ФГОС:
Студент должен
уметь:
- решать системы линейных уравнений.
знать:
- основы математического анализа, линейной алгебры и аналитической геометрии.
Оборудование: рабочая тетрадь, ручка, методические рекомендации по выполнению практической работы, справочная литература.
Методические указания по выполнению работы:
1. Ознакомиться с теоретическим материалом по практической работе.
2. Рассмотрите образцы решения задач по теме.
3.Выполнить предложенное задание согласно варианту по списку группы.
4.Изучить условие заданий для практической работы и выполнить её.
5. Ответить на контрольные вопросы даются письменно, после решения заданий в тетради для практических работ. Во время выполнения работы обучающийся может пользоваться своим конспектом, а также учебной литературой и справочным материалом.
5. Оформить отчет о работе. Сделайте вывод.