Уравнение прямой, проходящей через точку в данном направлении
Уравнение прямой, проходящей через т.у А(ха; уа) и имеющей угловой коэффициент k, записывается в виде
у – уа=k (x – xa). (5)
Уравнение прямой, проходящей через две точки
Уравнение прямой, проходящей через две точки т. А (х1; у1) и т.В (х2; у2), имеет вид
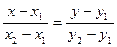 (6)
(6)
Если точки А и В определяют прямую, параллельную оси Ох (у1 = у2) или оси Оу (х1 = х2), то уравнение такой прямой записывается соответственно в виде:
у = у1 или х = х1 (7)
Нормальное уравнение прямой
Пусть дана прямая С, проходящая через данную точку Мо(Хо; Уо) и перпендикулярная вектору 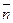 (А;В). Любой вектор
(А;В). Любой вектор 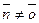 , перпендикулярный данной прямой
, перпендикулярный данной прямой 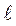 , называется ее нормальным вектором. Выберем на прямой произвольную т. М(х;у). Тогда
, называется ее нормальным вектором. Выберем на прямой произвольную т. М(х;у). Тогда 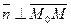 , а значит их скалярное произведение
, а значит их скалярное произведение 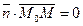 . Это равенство можно записать в координатах
. Это равенство можно записать в координатах
А( х-хо )+В( у-уо )=0 (8)
Уравнение (8) называется нормальным уравнением прямой.
Параметрическое и каноническое уравнения прямой
Пусть прямая l задана начальной точкой М0 (х0; у0) и направляющим вектором 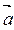 (а1;а2),. Пусть т. М(х ; у) – любая точка, лежащая на прямой l . Тогда вектор
(а1;а2),. Пусть т. М(х ; у) – любая точка, лежащая на прямой l . Тогда вектор 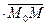 коллинеарен вектору
коллинеарен вектору 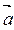 . Следовательно,
. Следовательно, 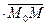 =
= 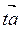 . Записывая это уравнение в координатах, получаем параметрическое уравнение прямой
. Записывая это уравнение в координатах, получаем параметрическое уравнение прямой
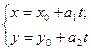 (9)
(9)
Исключим параметр t из уравнения (9). Это возможно, так как вектор 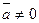 , и потому хотя бы одна из его координат отлична от нуля.
, и потому хотя бы одна из его координат отлична от нуля.
Пусть 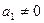 и
и 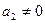 , тогда
, тогда 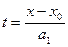 ,
, 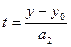 и, следовательно,
и, следовательно,
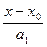 =
= 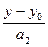 . (10)
. (10)
Уравнение (10) называется каноническим уравнением прямой с направляющим вектором
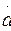 =(а1; а2). Если а1 =0 и
=(а1; а2). Если а1 =0 и 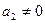 , то уравнения (9) примут вид
, то уравнения (9) примут вид
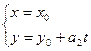 .
.
Этими уравнениями задается прямая, параллельная оси, Оу и проходящая через точку
М0 (х0; у0). Каноническое уравнение такой прямой имеет вид
х=х0 (11)
Если 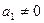 ,
, 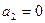 , то уравнения (9) примут вид
, то уравнения (9) примут вид
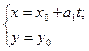
Этими уравнениями задается прямая, параллельная оси Ох и проходящая через точку
М0 (х0; у0). Каноническое уравнение такой прямой имеет вид
у=у0  (12)
(12)
Угол между прямыми. Условие параллельности и перпендикулярности двух
Прямых
Пусть даны две прямые, заданные общими уравнениями:
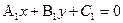 и
и 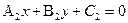
Тогда угол φ между ними определяется по формуле:
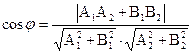 (13)
(13)
Условие параллельности 2-х прямых: 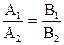 (14)
(14)
Условие перпендикулярности 2-х прямых: 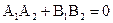 (15)
(15)
Условие параллельности в этом случае имеет вид: 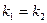 (17)
(17)
Условие перпендикулярности прямых: 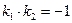 (18)
(18)
Если две прямые заданы каноническими уравнениями:
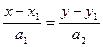 и
и 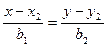
то угол φ между этими прямыми определяется по формуле:
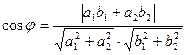 (19)
(19)
Условие параллельности прямых: 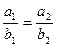 (20)
(20)
Условие перпендикулярности прямых: 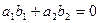 (21)
(21)
Расстояние от точки до прямой
Расстояние d от точки М(х1; у1) до прямой Ax+By+C=0 вычисляется по формуле
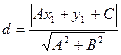 (22)
(22)
Пример по выполнению практической работы
Пример 1. Построить прямую 3х–2у+6=0.
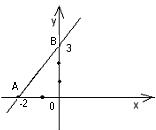
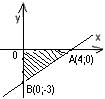
Решение:Для построения прямой достаточно знать какие-либо две её точки, например, точки её пересечения с осями координат. Точку А пересечения прямой с осью Ох можно получить, если в уравнении прямой принять у=0.Тогда имеем 3х+6=0, т.е. х=-2. Таким образом, А(–2;0).
Тогда В пересечения прямой с осью Оу имеет абсциссу х=0; следовательно, ордината точки В находится из уравнения –2у+6=0, т.е. у=3. Таким образом, В(0;3).
Пример 2. Составить уравнение прямой, которая отсекает на отрицательной полуплоскости Оу отрезок, равный 2 единицам, и образует с осью Ох угол φ =30˚.
Решение: Прямая пересекает ось Оу в точке В (0;–2) и имеет угловой коэффициент k=tg φ= = 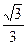 . Полагая в уравнении (2) k=
. Полагая в уравнении (2) k= 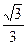 и b = –2, получим искомое уравнение
и b = –2, получим искомое уравнение
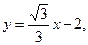 или
или 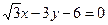 .
.
Пример 3. Составить уравнение прямой, проходящей через точки А (–1; 2) и
В (0;–3). (указание: угловой коэффициент прямой находится по формуле (3))
Решение: 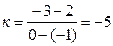 .Отсюда имеем
.Отсюда имеем 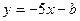 . Подставив в это уравнение координаты т.В, получим:
. Подставив в это уравнение координаты т.В, получим: 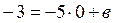 , т.е. начальная ордината b = –3 . Тогда получим уравнение
, т.е. начальная ордината b = –3 . Тогда получим уравнение 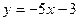 .
.
Пример 4.Общее уравнение прямой 2х – 3у – 6 = 0 привести к уравнению в отрезках.
Решение: запишем данное уравнение в виде 2х – 3у=6 и разделим обе его части на свободный член: 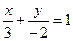 . Это и есть уравнение данной прямой в отрезках.
. Это и есть уравнение данной прямой в отрезках.
Пример 5.Через точку А (1;2) провести прямую, отсекающую на положительных полуосях координат равные отрезки.
Решение: Пусть уравнение искомой прямой имеет вид 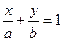 По условию а=b. Следовательно, уравнение принимает вид х + у = а. Так как точка А (1; 2) принадлежит этой прямой, значит ее координаты удовлетворяют уравнению х + у = а; т.е. 1 + 2 = а, откуда а = 3. Итак, искомое уравнение записывается следующим образом: х + у = 3, или х + у – 3 = 0.
По условию а=b. Следовательно, уравнение принимает вид х + у = а. Так как точка А (1; 2) принадлежит этой прямой, значит ее координаты удовлетворяют уравнению х + у = а; т.е. 1 + 2 = а, откуда а = 3. Итак, искомое уравнение записывается следующим образом: х + у = 3, или х + у – 3 = 0.
Пример 6. Для прямой 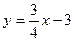 написать уравнение в отрезках. Вычислить площадь треугольника, образованного этой прямой и осями координат.
написать уравнение в отрезках. Вычислить площадь треугольника, образованного этой прямой и осями координат.
Решение: Преобразуем данное уравнение следующим образом: 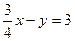 , или
, или 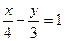 .
.
В результате получим уравнение 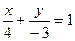 , которое и является уравнением данной прямой в отрезках. Треугольник, образованный данной прямой и осями координат, является прямоугольным треугольником с катетами, равными 4 и 3, поэтому его площадь равна S=
, которое и является уравнением данной прямой в отрезках. Треугольник, образованный данной прямой и осями координат, является прямоугольным треугольником с катетами, равными 4 и 3, поэтому его площадь равна S= 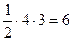 (кв. ед.)
(кв. ед.)
Пример 7. Составить уравнение прямой, проходящий через точку (–2; 5) и образующей с осью Ох угол 45º.
Решение: Угловой коэффициент искомой прямой k= tg 45º = 1. Поэтому, воспользовавшись уравнением (5), получаем у – 5 = x – (–2), или х – у + 7 = 0.
Пример 8. Составить уравнение прямой, проходящей через точки А(–3; 5)и В(7; –2).
Решение: Воспользуемся уравнением (6):
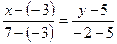 , или
, или 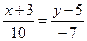 , откуда 7х + 10у – 29 = 0.
, откуда 7х + 10у – 29 = 0.
Пример 9. Проверить, лежат ли точки А(5; 2), В(3; 1) и С(–1; –1) на одной прямой.
Решение: Составим уравнение прямой, проходящей через точки А и С:
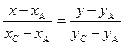 , или
, или 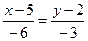
Подставляя в это уравнение координаты точки В (хВ= 3 и уВ = 1), получим (3–5) / (–6)= = (1–2) / (–3), т.е. получаем верное равенство. Т. о., координаты точки В удовлетворяют уравнению прямой (АС), т.е. 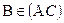 .
.
Пример 10: Составить уравнение прямой, проходящую через т. А(2;-3).
Перпендикулярную 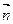 =(-1;5)
=(-1;5)
Решение: Пользуясь формулой (8), находим уравнение данной прямой -1(х-2)+5(у+3)=0,
или окончательно, х – 5 у - 17=0.
Пример 11: Даны точки М1 (2;-1) и М2(4; 5). Написать уравнение прямой, проходящей через точку М1 перпендикулярно вектору 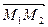 Решение: Нормальный вектор искомой прямой
Решение: Нормальный вектор искомой прямой 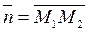 имеет координаты (2;6), следовательно по формуле (8) получим уравнение 2(х-2)+6(у+1)=0 или х+3у +1=0.
имеет координаты (2;6), следовательно по формуле (8) получим уравнение 2(х-2)+6(у+1)=0 или х+3у +1=0.
Пример 12: Вычислить угол между прямыми 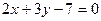 и
и 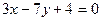 .
.
Решение: 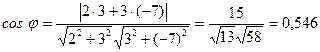 ;
; 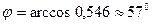 .
.
Пример 13: Выяснить взаимное расположение прямых:
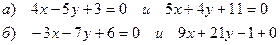
Решение: а) 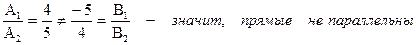 ;
;
б) 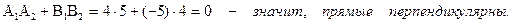
Пример 14: Вычислить угол между прямыми 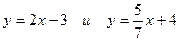
Решение: 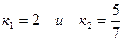
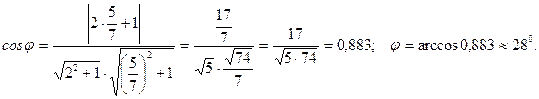
Пример 15: Выяснить взаимное расположение прямых:
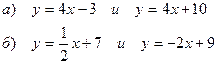
Решение: 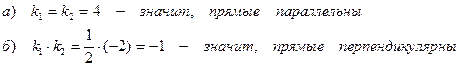
Пример 16:найти угол между прямыми 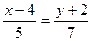 и
и 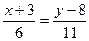 .
.
Решение: 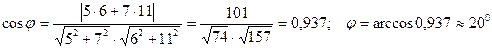 .
.
Пример 17:выяснить взаимное расположение прямых:
а) 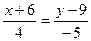 и
и 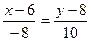 ;
;
б) 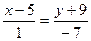 и
и 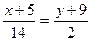 .
.
Решение:а) 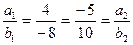 - прямые параллельны;
- прямые параллельны;
б) 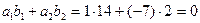 - значит, прямые перпендикулярны.
- значит, прямые перпендикулярны.
Пример 18:Вычислить расстояние от точки М(6; 8) до прямой 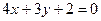
Решение: по формуле (22) получим: 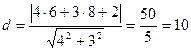 .
.
Задания для практического занятия:
Вариант 1
1. Привести общее уравнение прямой 2x+3y-6=0 к уравнению в отрезках и вычислить площадь треугольника, отсекаемого этой прямой от соответствующего координатного угла;
2. В ∆ABC вершины имеют координаты точки А (-3;4), точки В (-4;-3), точки С (8;1). Составить уравнения стороны (AB), высоты (ВК) и медианы (CМ);
3. Вычислить угловой коэффициент прямой, проходящей через точку М0 (-2;4) и параллельной вектору 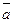 (6;-1);
(6;-1);
4. Вычислить угол между прямыми
а) 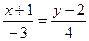 и
и 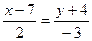 ; б)
; б) 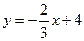 и
и 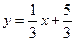 ;
;
5. Определить взаимное расположение 2-х прямых 2x – 5y – 20 = 0 и 5x + 2y – 10 = 0;
6. Вычислить расстояние от середины отрезка АВ до прямой 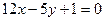 , если известны координаты концов отрезка т.А(1; 6) и т.В(9; 8).
, если известны координаты концов отрезка т.А(1; 6) и т.В(9; 8).
Вариант 2
1. Привести общее уравнение прямой 3x-4y+12=0 к уравнению в отрезках и вычислить длину отрезка, который отсекается от этой прямой соответствующим координатным углом;
2. В ∆ABC вершины имеют координаты точки А (4;2), точки В (1;5), точки
С (-2;6). Составить уравнения стороны (AB), высоты (ВК) и медианы (CМ);
3. Вычислить угловой коэффициент прямой, проходящей через точку М0 (3;-4) и параллельной вектору 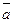 (-7;5);
(-7;5);
4. Вычислить угол между прямыми:
а) 2x - 3y + 7 = 0 и 3x - y + 5 = 0 ; б) 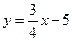 и y = 2x – 4;
и y = 2x – 4;
5.Определить взаимное расположение 2-х прямых 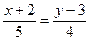 и
и 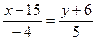 ;
;
6. Вычислить расстояние от середины отрезка АВ до прямой 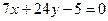 , если известны координаты концов отрезка т.А(18;8) и т.В(-2; -6).
, если известны координаты концов отрезка т.А(18;8) и т.В(-2; -6).
Вариант 3
1. Привести общее уравнение прямой 4x-5y+20=0 к уравнению в отрезках и вычислить площадь треугольника, отсекаемого этой прямой от соответствующего координатного угла;
2. В ∆ABC вершины имеют координаты точки А (3;-2), точки В (7;3), точки
С (0;8). Составить уравнения стороны (AB), высоты (ВК) и медианы (CМ);
3. Вычислить угловой коэффициент прямой, проходящей через точку M0 (-1;-2) и
параллельной вектору 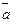 (3;-5);
(3;-5);
4. Вычислить угол между прямыми
а) 3x + y - 7 = 0 и x - y + 4 = 0; б) 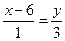 и
и 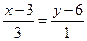 ;
;
5. Определить взаимное расположение 2-х прямых 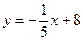 и y = 5x + 3;
и y = 5x + 3;
6. Вычислить расстояние от середины отрезка АВ до прямой 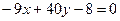 , если известны координаты концов отрезка т.А(4;-3) и т.В(-6; 5).
, если известны координаты концов отрезка т.А(4;-3) и т.В(-6; 5).
Вариант 4
1. Привести общее уравнение прямой 12x-5y+60=0 к уравнению в отрезках и вычислить длину отрезка, который отсекается от этой прямой соответствующим координатным углом;
2. В ∆ABC вершины имеют координаты точки А (0;-2), точки В (3;6), точки С (1;-4). Составить уравнения стороны (AB), высоты (ВК) и медианы (CМ);
3. Вычислить угловой коэффициент прямой, проходящей через точку M0(4;4) и параллельной вектору 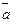 (-2;7);
(-2;7);
4.Вычислить угол между прямыми
а) x +4 y + 8 = 0 и 7x - 3y + 5 = 0; б) 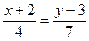 и
и 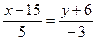 ;
;
5. Определить взаимное расположение 2-х прямых 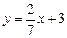 и
и 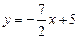 ;
;
6. Вычислить расстояние от середины отрезка АВ до прямой 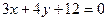 , если известны координаты концов отрезка т.А(-4; 8) и т.В(0; 4).
, если известны координаты концов отрезка т.А(-4; 8) и т.В(0; 4).
Контрольные вопросы
1. Назовите уравнения прямой на плоскости, когда известны точка, через которую она проходит и ее направляющий вектор;
2. Какой вид имеет нормальное, общее уравнения прямой на плоскости;
3. Назовите уравнение прямой, проходящей через две точки, уравнение прямой в отрезках, уравнение прямой с угловым коэффициентом;
4. Перечислите формулы для вычисления угла между прямыми, заданными уравнениями с угловым коэффициентом. Сформулируйте условия параллельности и перпендикулярности двух прямых.
5. Как найти расстояние от точки до прямой?
