Раздел 2. Введение в линейную алгебру.

Тема 2.1. Векторы на плоскости и в пространстве.

Практическая работа № 6 -7

Тема: «Составление уравнений прямых и плоскостей. Определение взаимного расположения прямой и плоскости.»

Цель работы:научиться составлять различные уравнения прямых на плоскости,

определять их взаимное положение.

Образовательные результаты, заявленные во ФГОС:

Студент должен

уметь:

- решать задачи, используя уравнения прямых и кривых

второго порядка на плоскости.

знать:

- основы математического анализа, линейной алгебры и

аналитической геометрии.

Оборудование: рабочая тетрадь, ручка, методические рекомендации по выполнению практической работы, справочная литература.

Методические указания по выполнению работы:

1. Ознакомиться с теоретическим материалом по практической работе.

2. Рассмотрите образцы решения задач по теме.

3.Выполнить предложенное задание согласно варианту по списку группы.

4.Изучить условие заданий для практической работы и выполнить её.

5. Ответить на контрольные вопросы даются письменно, после решения заданий в тетради для практических работ. Во время выполнения работы обучающийся может пользоваться своим конспектом, а также учебной литературой и справочным материалом.

5. Оформить отчет о работе. Сделайте вывод.

Краткие теоретические и учебно-методические материалы по теме практической работы

Общее уравнение прямой

Если на плоскости произвольно взята декартова система координат, то всякое уравнение первой степени относительно текущих координат x и y

Ax+By+C=0,(1)

где A и B одновременно не равны нулю, определяет прямую в этой системе координат.

Верно и обратное утверждение: в декартовой системе координат всякая прямая может быть представлена уравнением первой степени вида (1). Уравнение (1) называется общим уравнением прямой. Частные случаи уравнения (1) приведены в следующей таблице.

Значение коэффициентов	Уравнение прямой	Положение прямой
С=0 А=0 В=0 А=0, С=0 В=0, С=0	Ах+Ву=0 у=b, где b= -С / В x=a, где a= -C / A y=0 x=0	Проходит через начало координат Параллельна оси Ох Параллельна оси Оу Совпадает с осью Ох Совпадает с осью Оу

Угловой коэффициент прямой. Уравнение прямой с угловым коэффициентом и начальной ординатой

Углом наклона прямой к оси Ох называется наименьший угол φ, на который нужно повернуть в положительном направлении ось абсцисс до её совпадения с данной прямой. Направление любой прямой характеризуется её угловым коэффициентом k, который определяется как тангенс угла наклона φ этой прямой к оси Ох, т.е. k=tg φ. Исключения составляет лишь прямая, перпендикулярная оси Ох, которая не имеет углового коэффициента.

Уравнение прямой, имеющей угловой коэффициент k и пересекающий ось Оу в точке, ордината которой равна b (начальная ордината),записывается в виде:

y=kx+b. (2)

Угловой коэффициент k прямой, заданной уравнением Ax+By+C=0, находится как коэффициент k прямой, заданной двумя точками А(ха; уа) и В(хВ;уВ), вычисляется по формуле:

(3)

Уравнение прямой в отрезках

Уравнением прямой в отрезках называетсяуравнение вида:

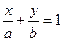(4)

где а и b – абсцисса и ордината точек пересечения прямой с осями Ох и Оу, т.е. длины

отрезков, отсекаемых прямой на координатных осях, взятые с соответствующими знаками.