Раздел ii. введение в общую алгебру

Лекция № 5. Элементы общей алгебры.

1. Свойства бинарных алгебраических операций.

Определение. На множестве А определена алгебраическая операция,если каждым двум элементам этого множества, взятым в определенном порядке, однозначным образом поставлен в соответствие некоторый третий элемент из этого же множества.

Примерами алгебраических операций могут служить такие операции как сложение и вычитание целых чисел, сложение и вычитание векторов, матриц, умножение квадратных матриц, векторное умножение векторов и др.

Отметим, что скалярное произведение векторов не может считаться алгебраической операцией, т.к. результатом скалярного произведения будет число, и числа не относятся к множеству векторов, к которому относятся сомножители.

Замечание. Вообще говоря, операция, определённая таким образом, называется бинарной, поскольку в ней участвуют два элемента. Но также можно говорить об унарных операциях, в которых участвует только один элемент данного множества, и в соответствие ему однозначным образом поставлен второй элемент этого множества. Таковы, например, операции извлечения корня квадратного или нахождения модуля числа.

Аналогично можно определить тринарную и прочие операции на данном множестве, в зависимости от количества участвующих в них элементов. В общем случае, 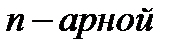операцией на множестве 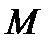будем называть функцию типа .

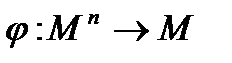Определение. Операция 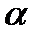, отображающая любой элемент множества 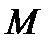в себя, называется тождественной операцией.

Тождественной операцией на множестве 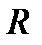, например, является умножение на единицу.

Для того чтобы описанные ниже соотношения выглядели бы более привычно, положим результат применения бинарной операции 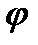элементам 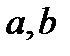записывать не в функциональном виде 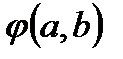, а виде 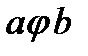, принятом для записи арифметических операций.

Определение. Операция 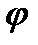называется коммутативной, если для любых элементов 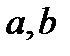выполняется: .

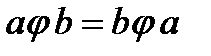Операции сложения и умножения чисел коммутативны, а вычитание и деление некоммутативны. Также некоммутативна операция умножения матриц (как известно из курса линейной алгебры).

Определение. Операция 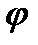называется ассоциативной, если для любых элементов 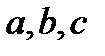выполняется: .

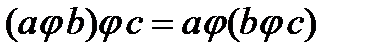Выполнение условия ассоциативности означает, что скобки в выражении 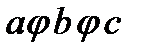можно не расставлять. Сложение и умножение чисел ассоциативны, что и позволяет не ставить скобки в выражениях типа 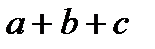и . В качестве примера неассоциативной операции можно привести возведение в степень:

.

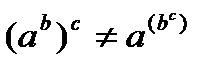Правда, запись 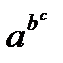является допустимой, но служит сокращением записи выражения 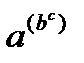, а не 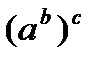(сокращённая запись которого - 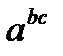). Важным примером ассоциативной операции является композиция отображений.

Определение. Операция 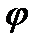называется дистрибутивной слева относительно операции 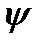, если для любых 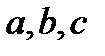выполняется:

,

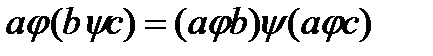и дистрибутивной справа относительно операции 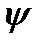, если для любых 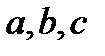выполняется:

.

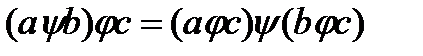Наличие свойства дистрибутивности позволяет раскрывать скобки. Например, умножение дистрибутивно относительно сложения (и вычитания) и справа, и слева:

.

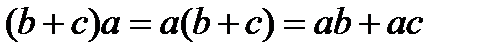Возведение в степень дистрибутивно относительно умножения справа: 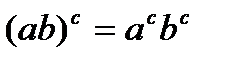, но не слева: 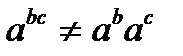. Сложение (и вычитание) чисел недистрибутивно относительно умножения: 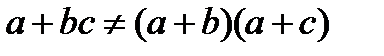. Ниже будет показано, что операции пересечения и объединения множеств дистрибутивны относительно друг друга и слева, и справа.

2. Алгебраические структуры.

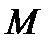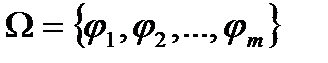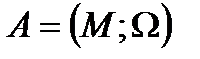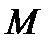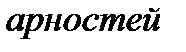Определение. Пусть дано некоторое множество , на котором задана совокупность операций . Структура вида называется алгеброй; множество называется несущим множеством, совокупность операций - сигнатурой, вектор “ ” операций 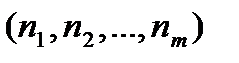называется типом.

Определение. Множество 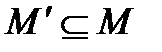называют замкнутым относительно 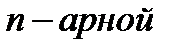операции 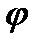на множестве 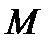, если значения функции 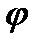на аргументах 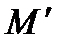принадлежат 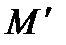(то есть 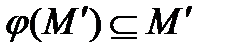). Если множество 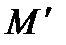замкнуто относительно всех операций 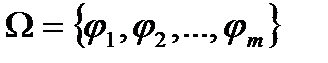, то структура 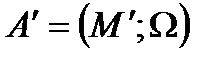называется подалгеброй алгебры .

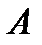Пример 1.

а) Алгебра 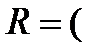R 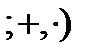называется полем действительных чисел (определение понятия поля будет дано ниже). Её тип - 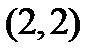. Это означает, что сигнатура данной алгебры содержит две бинарные операции. Здесь все конечные подмножества (кроме множества 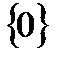) не замкнуты относительно обеих операций и, следовательно, не могут образовывать подалгебры. Но алгебра вида 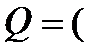Q 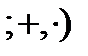-поле действительных чисел – образует подалгебру.

б) Пусть задано множество 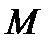. Множество всех его подмножеств – булеан, обозначается как 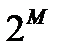или 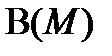. Алгебра 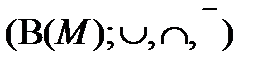называется булевой алгеброй множеств над множеством 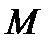. Её тип: 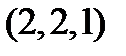. Для любого 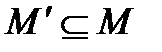будет являться подалгеброй .

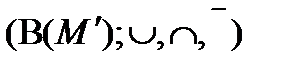в) Множество 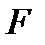одноместных функций на 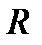(то есть функций 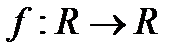вместе с унарной операцией дифференцирования является алгеброй. Множество элементарных функций замкнуто относительно этой операции (поскольку производная любой элементарной функции есть также элементарная функция), поэтому образует подалгебру данной алгебры.

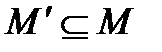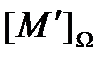Определение. Замыканием множества относительно сигнатуры (обозначается ) называется множество всех элементов, которые можно получить из элементов этого множества, применяя операции из сигнатуры (включая сами элементы ).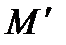

Например, в алгебре целых чисел 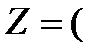Z 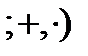замыканием числа 2 является множество чётных чисел.

Теорема 5.1. Непустое пересечение подалгебр образует подалгебру.

1. Гомоморфизм и изоморфизм.

Алгебры с различными типами (в смысле, определённом в пункте 1), очевидно, имеют существенно различное строение. Если же алгебры имеют одинаковый тип, то наличие у них сходства характеризуется вводимых ниже понятий.

Определение. Пусть даны две алгебры 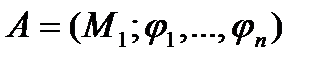и 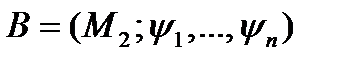. Гомоморфизмом алгебры 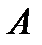в алгебру 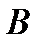называется функция 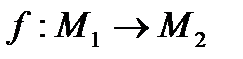, такая, что для всех 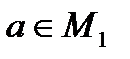выполняется условие:

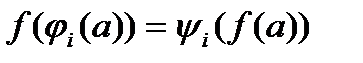для любого . (*)

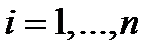Смысл данного определения состоит в следующем. Независимо от того, выполнена ли сначала операция 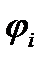в алгебре 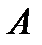, а потом произведено отображение 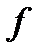, либо сначала произведено отображение 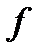, а потом в алгебре 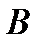выполнена соответствующая операция 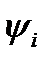, результат будет одинаков.

Сейчас мы определим некоторые виды гомоморфизма, обладающие дополнительными свойствами.

Определение. Гомоморфизм, который является инъекцией, называется мономорфизмом.

Определение. Гомоморфизм, который является сюръекцией, называется эпиморфизмом.

Определение. Гомоморфизм, который является биекцией, называется изоморфизмом.

Таким образом, можно сказать, что изоморфизм – это взаимно однозначный гомоморфизм.

Замечание. Если множества-носители двух данных алгебр равны, то их гомоморфизм называется эндоморфизмом, а изоморфизм – автоморфизмом.

Теорема 5.2. Есл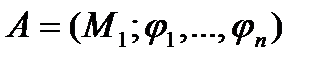и и 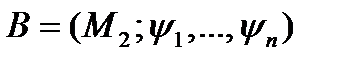- две алгебры одного типа и 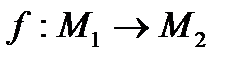- изоморфизм, то 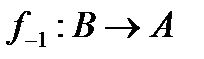- тоже изоморфизм.

Пример 2.

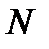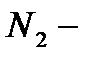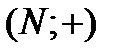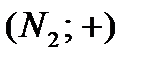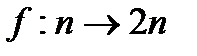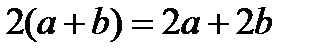а) Пусть - множество натуральных чисел, множество натуральных чётных чисел. Алгебры и изоморфны; изоморфизмом является отображение , причём условие здесь имеет вид . Поскольку 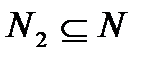, то данный изоморфизм есть изоморфизм алгебры 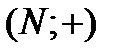в себя.

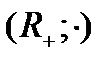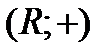б) Изоморфизмом между алгебрами и является, например, отображение 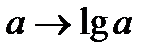. Условие имеет вид .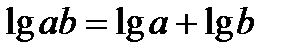

в) Булевы алгебры, образованные двумя различными множествами одинаковой мощности, изоморфны: операции у них просто одинаковы (см. выше), а отображением 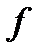может служить любое взаимнооднозначное соответствие.

Теорема 5.3. Отношение изоморфизма является отношением эквивалентности на множестве алгебр.

Понятие изоморфизма является одним из важнейших понятий в математике. Его сущность можно выразить следующим образом. Если две алгебры изоморфны, то элементы и операции любой из них можно переименовать таким образом, что эти алгебры совпадут. Это позволяет, получив некоторое эквивалентное соотношение в данной алгебре, распространять его на любую изоморфную ей алгебру. Распространённое в математике выражение “с точностью до изоморфизма” означает, что рассматриваются только те свойства объектов, которые сохраняются при изоморфизме, то есть являются общими для всех изоморфных объектов. В частности, изоморфизм сохраняет коммутативность, ассоциативность и дистрибутивность.