Уравнение движения в интегральной форме

Основой для вывода уравнения служит соотношение между работой и энергией, вытекающее из теоремы об изменении кинетической энергии системы: , которое можно представить в виде равенства . В этом равенстве: – текущее значение кинетической энергии, – начальное значение кинетической энергии, – работа движущих сил, выполненная от начального до текущего момента времени, – работа сил сопротивления, выполненная за то же время.

Величины энергий и работ определяются следующими равенствами:

, , , .

Подставляя эти выражения в вышезаписанное равенство, получаем окончательный вид уравнения:

.

В правой части уравнения подынтегральные выражения представляют собой функции от угла поворота кривошипа, т.е. перемещения. Это значит, что данные функции могут быть определены, только если внешние силы также зависят от перемещений. Данное обстоятельство определяет область применения уравнения в интегральной форме.

Уравнение в дифференциальной форме

Внешние силы, действующие в машинах, могут зависеть не только от перемещений, но и от скоростей, и от времени. В этих случаях уравнение в интегральной форме неприменимо. Для исследования динамики таких машин применяют более универсальное уравнение –уравнение в дифференциальной форме. Оно может быть получено из уравнения в интегральной форме путём дифференцирования по .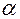

.

Сделав замену и затем, выполнив несложные преобразования, получим окончательно .

Первое слагаемое левой части представляет собой момент сил инерции, как следствие изменения . Второе слагаемое представляет также момент сил инерции, но как результат изменения .

Назначение и приближённое определение

Момента инерции маховика

Маховик служит для уменьшения колебаний величины угловой скорости ведущего звена, уменьшения угловых ускорений и, в конечном итоге, инерционных воздействий. Этот эффект, называемый кинематическим, тем больше, чем больше момент инерции маховика. Кинематический эффект тесно связан с динамическим, который заключается в том, что маховик выступает как аккумулятор кинетической энергии. Он накапливает кинетическую энергию в те промежутки времени, когда возрастает его угловая скорость, принимая на себя часть избыточной работы, которая в этом случае не тратится на разгон машины. При уменьшении угловой скорости маховик отдаёт часть накопленной энергии, помогая движущим силам выполнять полезную работу и препятствуя существенному уменьшению угловой скорости. Некоторые машины, например машины ударного действия, без такой помощи не смогли бы функционировать.

Для расчёта момента инерции маховика примем допущение, что максимальный перепад кинетической энергии машины, численно равный максимальному перепаду избыточной работы, поглощается маховиком. Для иллюстрации этого служит рис. 6.6. Допущение здесь заключается в том, что часть кинетической энергии поглощается звеньями механизма, чем мы пренебрегаем. Обозначим перепад избыточной работы . Согласно принятому допущению эта величина составляет разность между максимальным и минимальным значениями кинетической энергии маховика: ,

то есть .

Максимальная величина кинетической энергии маховика вычисляется по формуле

,

минимальная величина вычисляется по формуле

.

Поэтому разность этих величин даёт выражение

.

Разложив разность квадратов в скобках на множители и заменив последние их выражениями, полученными из приведенных выше формул для вычисления и , получаем

.

Объединяя результаты выкладок, запишем и , откуда окончательно получаем

.

Как видно из этой формулы, достичь полного постоянства угловой скорости невозможно, так как для этого необходимо иметь бесконечно большой маховик (требуется ). Ясно также, что увеличение скорости вращения маховика ведёт к уменьшению его массы и размеров, поэтому целесообразно маховик устанавливать на более быстроходный вал.

Вопросы для самопроверки

1. Какие задачи решаются при исследовании динамики машин?

2. Что представляет собой динамическая модель машины?

3. Что называется приведённым моментом инерции механизма?

4. Что называется приведённым моментом сил?

5. Какая теорема механики положена в основу уравнений динамики машин?

6. Как записать кратчайшую форму уравнения динамики?

7. Какие существуют виды (режимы) движения машин?

8. Чем характеризуются пуск, остановка и установившийся режим работы машин?

9. Что такое коэффициент неравномерности движения машины?

10. Как определяется средняя величина угловой скорости ведущего звена?

11. Для чего предназначен маховик в машине?

12. Какое допущение принято для приближённого определения момента инерции маховика?

13. В чём заключается кинематический и динамический эффект действия маховика?

14. Как определяется момент инерции маховика?

Библиографический cписок

1. Артоболевский И.И Теория механизмов и машин. М., 1988. 640 с.

2. Фролов К.В., Попов С.А., Мусатов А.К. и др. Теория механизмов и машин / Под ред. К.В.Фролова. М., 1987. 496 с.

3. Юдин В.А., Петрокас Л.В.Теория механизмов и машин. М., 1977. 527 с.

4. Левитский Н.И. Теория механизмов и машин. М., 1979. 576 с.

5. Крайнев А.Ф. Словарь-справочник по механизмам. М., 1981. 438 с.

6. Кореняко А.С. Теория механизмов и машин. Киев, 1976. 444 с.

7. Левитская О.Н., Левитский Н.И. Курс теории механизмов и машин. М.,

1976. 269 с.

.

.