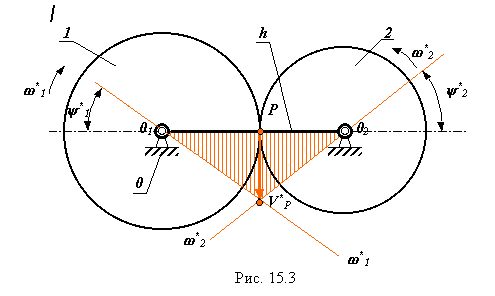
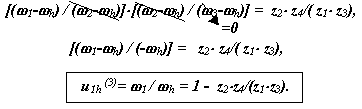Движение механизма относительно водила
То есть можно записать выражение, которое называется формулой Виллиса для планетарных механизмов
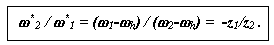
§ 4. Кинематическое исследование типовых планетарных механизмов графическим и аналитическим методами.
Двухрядный механизм с одним внутренним и одним внешним зацеплением.
Дано: Кинематическая схема механизма - ri, числа зубьев колес - zi ;
_______________________________________________
Определить: Передаточное отношение механизма - ?
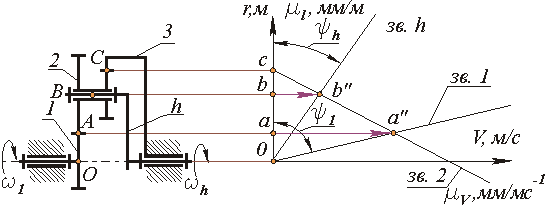
Рис.15.4
Аналитическое определение передаточного отношения.
В планетарном редукторе, изображенном на рис.15.4 на звене 2 нарезаны два зубчатых венца:
z2 , который зацепляется с зубчатым венцомz1 звена 1;
z3 , который зацепляется с внутренним зубчатыми венцом z4 звена 3.
По формуле Виллиса отношение угловых скоростей звеньев для внешнего зацепления колес z2 и z1
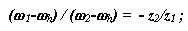
для внутреннего зацепления колес z4 и z3
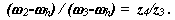
Перемножим, правые и левые части этих уравнений, и получим
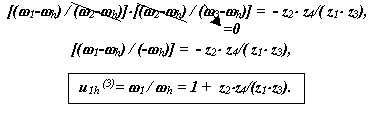
Графическое определение передаточного отношения.
В системе координат ri0V построим треугольники распределения линейных скоростей звеньев. Для этого из точки А с ординатой r1 в выбранном произвольном масштабе μV, мм/м∙с-1 отложим отрезок aa'. Через конец этого отрезка и начало координат проведем прямую, которая определит распределение скоростей для точек звена 1, лежащих на осиri. Эта прямая образует с осьюri угол ψ1. Так как в точке с скорости звеньев 2 и 3 равны между собой и равны нулю, то соединяя точку с с прямой с точкой a', получим линию распределения скоростей для звена 2. Так как точка принадлежит звеньям 2 и h, то ее скорость определяется по лучу сa' для радиуса равного rB = (r1+r2), что в масштабе μV, мм/м∙с-1 соответствует отрезку bb'. Соединяя точку b' с началом координат прямой, найдем линию распределения скоростей для водила. Эта линия образует с осью ri угол ψh. Передаточное отношение планетарного механизма определенное по данным графическим построениям можно записать так
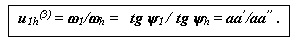
Однорядный механизм с одним внутренним и одним внешним зацеплением.
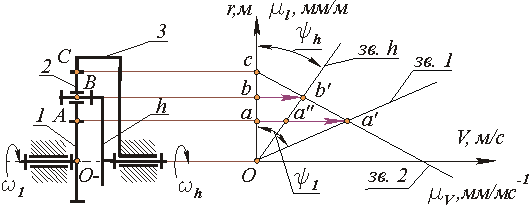
Рис.15.5
Аналитическое определение передаточного отношения.
По формуле Виллиса отношение угловых скоростей звеньев для внешнего зацепления колес z2 и z1 :
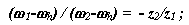
для внутреннего зацепления колес z2 и z3:
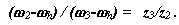
Перемножим, правые и левые части этих уравнений, и получим:
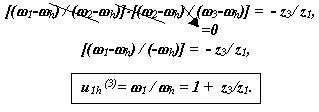
Графическое определение передаточного отношения.
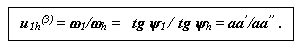
Двухрядный механизм с двумя внешними зацеплениями.
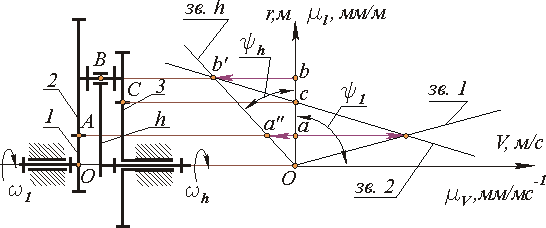
Рис.15.6
Аналитическое определение передаточного отношения.
В планетарном редукторе, изображенном на рис.15.6 на звене 2 нарезаны два зубчатых венца:
z2 , который зацепляется с зубчатым венцом z1 звена 1;
z3 , который зацепляется с внутренним зубчатыми венцомz4 звена 3.
По формуле Виллиса отношение угловых скоростей звеньев для внешнего зацепления колес z2и z1 :
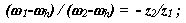
для внешнего зацепления колес z4 и z3:
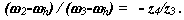
Перемножим, правые и левые части этих уравнений, и получим: