Привязка линии к диаграмме по КБВ и минимуму напряжения.

Ранее было показано (см. (4.2)), что входное сопротивление в сечениях линии, где формируются минимумы и максимумы напряжения, чисто вещественно и равно соответственно КБВ и КСВ в линии (см. (4.9), (4.8)):

Точки на круговой диаграмме, соответствующие этим значениям, должны, очевидно, находиться на пересечении кривых (вертикаль) и (минимум) или (максимум). На рис. 4.5 показаны точки, соответствующие минимуму напряжения при КБВ в линии, равном 0,5, и максимуму напряжения при КСВ в линии, равном 3. Верхнюю полуось на диаграмме сопротивлений часто называют линией минимумов, а нижнюю полуось – линией максимумов. При переходе от сопротивлений к проводимостям линии минимумов и максимумов меняются местами.

4.8. Определение сопротивления нагрузки по КБВ
и местоположению минимума напряжения

Допустим, в ИЛ экспериментально определено местоположение условных концов 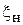. Если к концу ИЛ подключить нагрузку с некоторым неизвестным сопротивлением , то это сопротивление можно найти, определив КБВ в линии и местоположение минимума напряжения 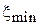относительно ближайших условных концов 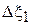и 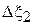. Отметим на круговой диаграмме точку 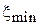соответствующую минимуму напряжения (пересечение верхней полуоси с окружностью известного КБВ или с окружностью ). Если теперь переместиться по окружности фиксированного КБВ на в сторону генератора или на в сторону нагрузки, придем в точки и на соответствующие условным концам. Так как условные концы находятся на расстоянии , от конца ИЛ, входное сопротивление в них равно 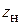(отрезки длиной сопротивления не трансформируют). Следовательно, по кривым и , проходящим по диаграмме через и , можно найт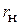и и 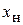(рис. 4.6).

Задача. Нагрузочный конец ИЛ находится справа от наблюдателя. Отсчеты по шкале перемещений ИЛ линейно возрастают от нагрузки к генератору. Отсчеты, соответствующие условным концам и минимуму, равны Измеренный .

Найдите ; ; направление перемещения по диаграмме для обоих случаев; нормированное сопротивление нагрузки.

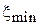Решение. Длина волны – удвоенное расстояние между соседними точками и : . Расстояние между и ближайшим Те же расстояния в долях длины волны: (перемещение по диаграмме к Г); (перемещение по диаграмме к Н). Построение показано на рис. 4.7. Найденное сопротивление нагрузки:

4.9. Включение в линию передачи трансформирующих отрезков
с волновым сопротивлением, отличным от волнового
сопротивления основного тракта

В технике СВЧ часто применяют устройства (трансформаторы, фильтры и т.п.), представляющие собой несколько последовательно включенных отрезков линий с различными волновыми сопротивлениями (рис. 4.8, а). На рис. 4.8, б показан простейший вариант такого включения: к основной линии, имеющей волновое сопротивление 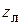, подключен отрезок линии длиной с волновым сопротивлением . К правому концу этого отрезка присоединена нагрузка с сопротивлением 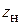. Возможной реализацией такой схемы может быть устройство, изображенное на рис. 4.8, в: в коаксиальном кабеле на участке длиной внутренний проводник утолщен, так что . К правому концу отрезка подключается линия с волновым сопротивлением 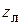, в общем случае несогласованная.

Задача. В устройстве, показанном на рис. 4.8: диэлектрик – воздух. Сопротивление Ом. Длина волны в основной линии и трансформирующем отрезке Найдите и .

Решение. 1. Прежде всего нужно рассчитать волновое сопротивление коаксиальных лини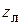й – и :

2. Далее следует найти сопротивление 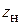нормированное к :

3. С помощью круговой диаграммы (рис. 4.9) определить входное сопротивление , нормированное к по найденному ранее сопротивлению 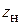в сечении А. Точка А на диаграмме ( ) соответствует сечению А в линии; отсчет по шкале перемещений: 0,23, КБВ = 0,36. Чтобы найти входное сопротивление в сечении В, нормированное к , т.е. , нужно переместиться к генератору на , т.е. до отсчета . Через точку В на диаграмме, соответствующую сечению В в линии, проходят кривые Таким образом, сопротивление , нормированное к , равно

4. Теперь легко завершить решение задачи:

Порядок выполнения работы

1. Определение местоположения условных концов линии и длины волны. Установив на конце ИЛ заглушку, определите отсчеты по шкале ИЛ, соответствующие двум соседним условным концам на частоте, заданной преподавателем. Определите длину волны в линии.

2. Измерение сопротивления нагрузки. Подключите к концу ИЛ нагрузку в виде последовательно включенных: гибкого кабеля, переменного аттенюатора и заглушки. Установите лимб аттенюатора на 60...80 делений. Измерьте КБВ в ИЛ и отсчет 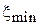соответствующий минимуму напряжения. Изобразите эскиз типа рис. 1.6. Рассчитайте относительные расстояния и . Пользуясь круговой диаграммой, определите 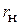и 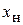в отчете необходимо поместить рисунок (типа рис. 4.7) с указанием всех числовых данных, получаемых при операциях на круговой диаграмме.

3. Измерение входного сопротивления плунжера. Подключите к концу ИЛ плунжер (Пл). Измерьте его входное сопротивление как функцию отсчета по шкале Пл. Методика измерений и обработки данных та же, что и в п. 2, однако КБВ определять не следует, так как заранее известно, что он равен нулю. Из двух определенных ранее условных концов выгодно выбрать тот, который находится ближе к генератору. Короткозамыкатель Пл перемещайте шагами начиная с отсчета, равного нулю. Полное перемещение должно быть порядка . Экспериментальные данные и результаты их обработки сведите в таблицу. Постройте график зависимости от отсчета по шкале Пл. Он должен иметь форму тангенсоиды (в общем случае смещенной – рис. 4.10). На графике найдите отсчет (отсчеты), соответствующий (на рис. 4.10 помечен крестом). Если принять этот отсчет за нулевой и откладывать вправо от него переменную 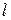, то график рис. 4.10 должен описываться функцией (теоретическая зависимость (4.14)). Рассчитайте эту функцию для . Результаты расчета сведите в таблицу. График нанесите на соответствующем участке экспериментального графика . Оцените степень совпадения графиков.

4. Трансформация сопротивления отрезком кабеля с увеличенным диаметром внутреннего проводника. Исследуется устройство, изображенное на рис. 4.8, б: между концом ИЛ и нагрузкой включается насадка диаметра . В качестве нагрузки используется плунжер. Получив насадку, измерьте ее размеры и . Сборку устройства проведите в следующем порядке: а) насадку сочлените с концом ИЛ; б) чтобы при дальнейших операциях насадка не уперлась в Короткозамыкатель Пл, отведите его на достаточное расстояние от входа Пл; в) освободите стопорный винт плунжера

и выдвиньте его внутренний проводник налево до упора; г) сочлените насадку с внутренним проводником Пл; д) осторожно перемещая корпус Пл налево, сочлените наружные проводники Пл и кабельного выхода ИЛ и надежно соедините их с помощью резьбового соединения; е) закрепите внутренний проводник Пл стопорным винтом.

Собранный узел выглядит, как на рис. 4.11. Для проведения эксперимента короткозамыкатель Пл нужно установить в определенное положение, обеспечив тем самым в сечении А некоторое известное сопротивление 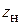. В п. 3 измерялось входное сопротивление плунжера, однако поскольку результаты этих измерений еще не обработаны, нет возможности задаваться сопротивлением 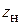. Поэтому из таблицы (проконсультировавшись с преподавателем) выбираем тот отсчет по шкале Пл, при котором минимум 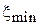в ИЛ находится на расстояниях либо либо от выбранного узла . При иных положениях короткозамыкателя Пл его входное сопротивление получится близким либо к нулю, либо к бесконечности, что в данном исследовании малоинтересно. Выбранный отсчет по шкале Пл обозначьте . Впоследствии при обработке таблицы Вы найдете соответствующее ему входное сопротивление , нормированное к 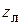. Ненормированное сопротивление , где – волновое сопротивление Пл и ИЛ.

Осталось правильно установить короткозамыкатель Пл. Обратите внимание, что в схеме рис. 4.11 при установке по шкале плунжера отсчета нужное сопротивление 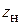получается на его входе, т. е. в сечении В, к тому же – только при отсутствии насадки. Чтобы получить сопротивление 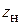в сечении А, короткозамыкатель нужно дополнительно сместить вправо на длину насадки , т. е. скорректированный отсчет по шкале Пл должен быть не , а .

Установив скорректированный отсчет по шкале Пл, найдите местоположение минимума 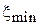в ИЛ (КБВ = 0 априорно), приведите эскиз устройства (типа рис. 4.11), рассчитайте значение относительных расстояни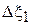й и 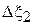и, пользуясь круговой диаграммой, определите в сечении В (см. рис. 4.10), т. е. на левом входе трансформирующего отрезка, совпадающем с концом ИЛ. В отчете необходимо поместить рисунок (типа рис. 4.7) с полным набором числовых данных, отражающих все этапы построений на круговой диаграмме. Для проверки совпадения теории с экспериментом рассчитайте теоретическое значение . Последовательность расчета такая же, как в задаче 4.9. Значение 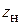берется из табл. п. 3 (она соответствует отсчету по шкале Пл). 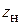Значение , входящее в расчет, равно .

В отчете приведите все вычисления по схеме задачи 4.9, а также эскиз (типа рис. 4.11). Полученное теоретическое значение сравните с экспериментальным.

4.11. Контрольные вопросы

1. Дайте определение входного нормированного и ненормированного сопротивления линии. Дайте обоснование физической интерпретации, Z_вх(z). От чего зависит входное сопротивление в сечении линии с координатой z? При каких условиях Z_вх неизменно вдоль линии?

2. Приведите формулу теории длинных линий, выражающую жесткую связь между Z_вх( 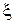) и 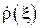. Опираясь на эту формулу и учитывая, что , покажите, что фаза входного сопротивления лежит в пределах –π/2…π/2.

3. Покажите, что период функции 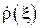равен λ/2. Покажите, что период функции Z_вх( 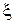) также равен λ/2. Покажите, что если коэффициент отражения равен по модулю единице, то входное сопротивление чисто мнимо.

4. Изобразите на комплексной плоскости диаграмму для векторов соответствующую сечению линии, где формируется максимум напряжения. Покажите, что входное сопротивление в этом сечении чисто вещественно и равно КСВ. Перейдите в сечение линии, смещенное к нагрузке на расстояние меньшее λ/4. Постройте векторную диаграмму для этого сечения и покажите, что сопротивление здесь по модулю меньше КСВ, а его фаза неотрицательна и не превосходит π/2.

5. Приведите эпюры распределения модуля и фазы нормированного входного сопротивления вдоль линии. Чему равны входные сопротивления в сечениях линии, где формируются максимум и минимум напряжения? Используя эпюры и φ_Z( 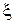), изобразите (на качественном уровне) эпюры для r_вх и x_вх .

6. Запишите формулу для входного сопротивления короткозамкнутой линии длиной l в произвольном сечений с координатой z. и эпюры распределения модуля комплексных амплитуд напряжения и тока, а также входного сопротивления.

7. Запишите формулу для входного сопротивления короткозамкнутой линии длиной l. При каких l входное сопротивление имеет индуктивный и емкостной характер? Чему равно входное сопротивление четвертьволновой и полуволновой короткозамкнутой линии? Поясните, почему при больших длинах l частотная зависимость входного сопротивления осциллирует быстрее, нежели при малых l?

8. Какой смысл вкладывается в понятие «трансформация сопротивления отрезком линии»? В каких случаях отрезок линии не трансформирует сопротивления?

9. Покажите, как по круговой диаграмме найти входное сопротивление в сечении 2, если оно известно в сечении 1.

10. Как, зная нормированное сопротивление в некотором сечении линии, найти нормированную проводимость в том же сечении? Приведите обоснование приема.

11. Где на круговой диаграмме находятся точки, соответствующие минимуму и максимуму напряжения? Ответ аргументируйте. Почему в условных концах линии входное сопротивление совпадает с сопротивлением нагрузки?

12. Поясните, почему на эквивалентной схеме кабеля со скачкообразным изменением диаметра внутреннего проводника должны присутствовать реактивные элементы в плоскостях скачков. При каких условиях этими элементами можно пренебречь?

13. Опишите последовательность действий при экспериментальном определении входного сопротивления произвольной нагрузки и при обработке результатов эксперимента.

14. Почему при определении входного сопротивления плунжера не нужно измерять КБВ? Почему график зависимости x_вх плунжера в функции отсчета по его шкале представляет собой тангенсоиду, причем смещенную?

15. Опишите порядок сборки узла «ИЛ – насадка – Пл» и приведите его эскиз.

16. Приведите эскиз узла «ИЛ – насадка – Пл», покажите сечения А и В и размер l_t. Допустим, измеряя входное сопротивление Пл, нормированное к его волновому сопротивлению Z_Л . Вы нашли, что оно равно jx_вх при отсчете l₀ по шкале Пл. Чему равно ненормированное сопротивление Z_H? Какой отсчет нужно установить по шкале Пл, чтобы обеспечить сопротивление Z_H в сечении А изображенного узла?

17. Какую величину КБВ следует ожидать в ИЛ при исследовании узла
«ИЛ – насадка – Плунжер»? Будет ли сопротивление в сечении В содержать вещественную часть? Ответ аргументируйте.

18. Изобразите (на качественном уровне) предполагаемый вид экспериментальных графиков входного сопротивления плунжера при малом и большом расстоянии между входом и короткозамыкателем в зависимости от частоты.

5. ВОЛНЫ В КОАКСИАЛЬНОЙ ЛИНИИ
ПРИ ПРОИЗВОЛЬНОЙ НАГРУЗКЕ

Цель работы: Исследование параметров отрезков коаксиальной линии при произвольной нагрузке в программе Microwave Office.

5.1. Поле Т-волны в коаксиальной линии

Главное свойство поля Т-волны – отсутствие продольных компонент электрического и магнитного полей. Т-волна может существовать только в линиях, образованных как минимум двумя однородными в продольном направлении проводниками. Электрическое поле Т-волны в поперечном сечении совпадает с решением электростатической задачи, потенциально (может быть представлено градиентом скаляра – потенциала), что дает возможность определить напряжение (разность потенциалов) между проводниками как работу сил поля при перемещении единичного положительного заряда по произвольному пути между проводниками, лежащему в плоскости поперечного сечения. Магнитное поле Т-волны в поперечном сечении линии совпадает с решением стационарной задачи для тока, протекающего по проводникам. Поэтому и в динамическом поле бегущей волны допустимо определение тока как циркуляции вектора напряженности магнитного поля по произвольному, но лежащему в плоскости поперечного сечения и охватывающему один из проводников контуру.

Т-волны не имеют дисперсии, скорость их всегда равна скорости света в среде, заполняющей линию.

Коаксиальная линия представляет один из наиболее распространенных типов линии с Т-волной. Коаксиальная линия образована двумя соосными цилиндрическими проводниками (рис. 5.1). В такой линии могут распространяться как основная Т-волна, так и волны высших типов. Если же l > p(R₁ + R₂), то высшие типы не распространяются и в линии представлена лишь основная Т-волна (одномодовый режим).

Поперечная структура поля Т-волны (рис. 5.2) довольно проста и обладает осевой симметрией. Как и положено поперечной волне, ее электрическое и магнитное поля не имеют продольных компонент. Силовые линии электрического поля направлены по радиусам, силовые линии магнитного поля образуют концентрические окружности. Поле отлично от нуля только во внутреннем пространстве между проводниками R₁ < r < R₂.

Часто вводят понятие электрической длины отрезка линии Q = kDz, где – длина отрезка линии.

Отношение амплитуд напряжения и тока в бегущей Т-волне дает значение волнового сопротивления Z_л.