Решение плохо обусловленных систем линейных алгебраических уравнений

I. ЦЕЛЬ РАБОТЫ

Приобретение навыков решения плохо обусловленных систем линейных алгебраических уравнений.

II. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

Рассмотрим систему линейных алгебраических уравнений.

где А — квадратная матрица размерностью 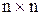; 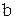—вектор свободных членов;

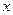
— искомый вектор

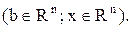
Если 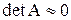, то система (1) называется плохо обусловленной. В этом случае погрешности коэффициентов матрицы и правых частей или погрешности округления при расчетах могут сильно исказить решение.

При решении многих задач правая часть системы (1) и коэффициенты матрицы А известны приближенно. При этом вместо точной системы (1) имеем некоторую другую систему

такую, что

Полагаем, что величины 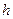и d известны.

Так как вместо системы (1) имеем систему (2), то можем найти лишь приближенное решение системы (1). Метод построения приближенного решения системы (1) должен быть устойчивым к малым изменениям исходных данных.

Псевдорешением системы (1) называется вектор 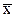, минимизирующий невязку 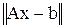на всем пространстве .

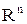Пусть х¹ –некоторый фиксированный вектор из 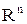, определяемый обычно постановкой задачи.

Нормальным относительно вектора х¹ решением системы (1) называется псевдорешение х⁰ с минимальной нормой 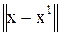, то есть

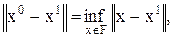
где F—совокупность всех псевдорешений системы (1).

Причем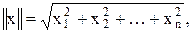

где 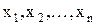¾компоненты вектора х.

Для любой системы вида (1) нормальное решение существует и единственно. Задача нахождения нормального решения плохо обусловленной системы (1) является некорректно поставленной.

Для нахождения приближенного нормального решения системы (1) воспользуемся методом регуляризации.

Согласно указанному методу построим сглаживающий функционал вида

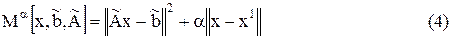
и найдем вектор 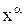, минимизирующий на 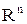этот функционал. Причем параметр регуляризации a однозначно определен из условия

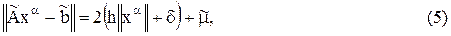
где .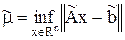

Вырожденные и плохо обусловленные системы могут быть неразличимы в рамках заданной точности. Но если имеется информация о разрешимости системы (1), то вместо условия (5) следует использовать следующее условие:

Компоненты 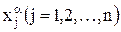вектора 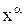являются решениями системы линейных алгебраических уравнений, которая получается из условия минимума функционала (4)

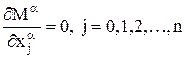
и имеет вид

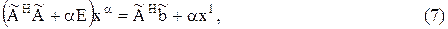
где Е—единичная матрица,

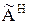¾эрмитово сопряженная матрица.

На практике для выбора вектора 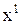нужны дополнительные соображения. Если их нет, то полагают 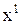=0.

Для 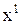=0 систему (7) запишем в виде

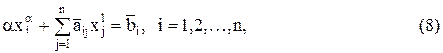
где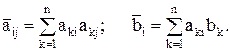

Найденный вектор 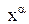будет являться приближенным нормальным решением системы (1).

Остановимся на выборе параметра a. Если a=0, то система (7) переходит в плохо обусловленную систему. Если a велико, то система (7) будет хорошо обусловлена, но регуляризованное решение не будет близким к искомому решению системы (1). Поэтому слишком большое или слишком малое a не пригодны.

Обычно на практике проводят расчеты с рядом значений параметра a. Например,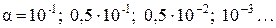

Для каждого значения a находят элемент 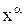, минимизирующий функционал (4). В качестве искомого значения параметра регуляризации берется такое число a, для которого с требуемой точностью выполняется равенство (5) или (6).

III. ЗАДАНИЕ

1. Построить систему линейных алгебраических уравнений, состоящую из трех уравнений с тремя неизвестными, с определителем, величина которого имеет порядок 10^-6.

2. Построить вторую систему, аналогичную первой, но имеющую другие свободные члены, отличающиеся от свободных членов первой системы на величину 0,00006.

3. Решить построенные системы методом регуляризации (полагая 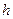=0 и d=10^-4) и каким-либо другим методом (например, методом Гаусса).

4. Сравнить полученные результаты и сделать выводы о применимости использованных методов.

IV. ОФОРМЛЕНИЕ ОТЧЕТА

В отчете должны быть представлены:

1. Название работы.

2. Постановка задачи.

3. Описание алгоритма (метода) решения.

4. Текст программы с описанием.

5. Результаты работы программы.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Тихонов А.Н., Арсенин В.Я. Методы решения некорректных задач. — М.: Наука, 1979. 286 с.

2. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. — М.: БИНОМ. Лаборатория Знаний, 2007 636с.

Лабораторная работа № 23