Приближенное вычисление интегралов

ПО ФОРМУЛЕ СИМПСОНА

IV. ЦЕЛЬ РАБОТЫ

Приобретение навыков приближенного вычисления интегралов с помощью квадратурных формул.

ΙΙ.ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

Пусть требуется вычислить интеграл .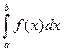

Разобьем отрезок 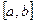с помощью равноотстоящих точек

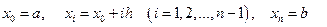
на 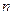равных частей. Шаг .

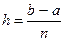Пусть = .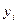

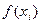Полагая в формулах Ньютона – Котеса

;

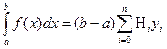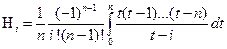
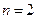, получаем

.

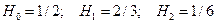Так как 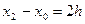, то

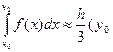
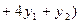. (1)

Это формула Симпсона.

Для повышения точности отрезок [a,b] разбивается на четное число частей 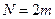. Тогда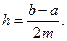

Интеграл разбивается на сумму интегралов. К каждому удвоенному промежутку длины 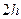применим формулу (1).

Получим обобщенную формулу Симпсона

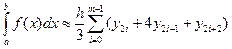. (2)

Для погрешности формулы Симпсона (2) справедлива оценка

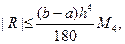
где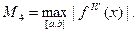

IIΙ.ЗАДАНИЕ

Вычислить с помощью формулы Симпсона определенный интеграл от заданной функции. Варианты заданий приведены в лабораторной работе № 11.

IV. Оформление отчета

В отчете должны быть представлены:

1. Название работы.

2. Постановка задачи.

3. Описание алгоритма (метода) решения.

4. Текст программы с описанием.

5. Результаты работы программы.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. — М.: БИНОМ. Лаборатория Знаний, 2007 636с.

2. Калиткин Н.Н. Численные методы. - М.: Наука, 1978. 512 с.

3. Демидович Б.П., Марон И.А. Основы вычислительной математики. - М.: Лань, 2009. 672 с.

Лабораторная работа № 13

ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ КРАТНЫХ

ИНТЕГРАЛОВ МЕТОДОМ ЯЧЕЕК

ЦЕЛЬ РАБОТЫ

Приобретение навыков приближенного вычисления кратных интегралов.

ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

Построим кубатурную формулу, предназначенную для приближенного вычисления двойных интегралов

Рассмотрим метод ячеек.

Пусть область интегрирования 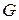представляет собой прямоугольник 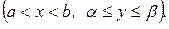Разобьем область 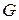на прямоугольные ячейки (рис. 1).

оо

ю

ююю

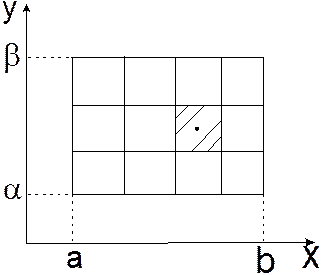
Рис. 1.

Используя формулу средних для вычисления интеграла по каждой ячейке и обозначая через 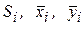соответственно площадь 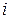ячейки и координаты ее центра, получим

Для любой непрерывной функции 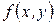интегральная сумма сходится к значению интеграла, когда периметры всех ячеек стремятся к нулю.

Если стороны прямоугольника разбиты соответственно на 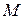и 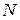равных частей, то погрешность обобщенной формулы (2)

В случае, когда область 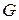не является прямоугольником, на нее следует наложить прямоугольную сетку (рис. 2).

Рис. 2

Ячейки, которые полностью лежат в области 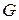, называются внутренними. Ячейка называется граничной, если часть ее принадлежит 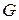, а часть находится вне 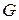. Площадь внутренней ячейки равна произведению ее сторон. Площадью граничной ячейки будем считать площадь той ее части, которая принадлежит 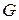. Эту площадь вычислим приближенно, заменяя истинную границу на хорду. Указанные выше площади подставим в формулу 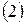и найдем приближенное значение интеграла.

ЗАДАНИЕ

Методом ячеек вычислить интеграл 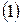по области 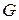, изображенной на рис. 3.

Рис. 3

Варианты заданий

Номер варианта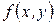

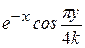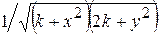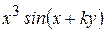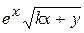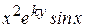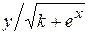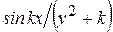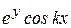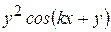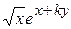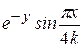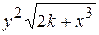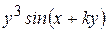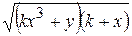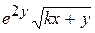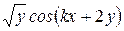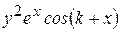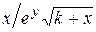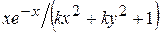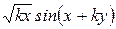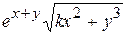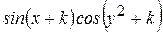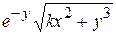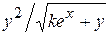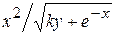Здесь 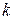- последняя цифра номера группы.

IV. Оформление отчета

В отчете должны быть представлены:

1. Название работы.

2. Постановка задачи.

3. Описание алгоритма (метода) решения.

4. Текст программы с описанием.

5. Результаты работы программы.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Калиткин Н.Н. Численные методы. - М.: Наука, 1978. 512 с.

2. Демидович Б.П., Марон И.А. Основы вычислительной математики. - М.: Лань, 2009. 672 с.

Лабораторная работа № 14