Вхождение функции в функцию. Импликанты

Понятием "минимизация переключательных функций" объединяется ряд процедур, выполнение которых направлено на получение наиболее компактной, минимальной в некотором смысле формы представления переключательной функции. Как правило, в качестве критерия минимальности переключательной функции используется число букв в логическом выражении. Действительно, любые две рядом стоящие буквы связаны между собой знаком какой-либо логической операции. Поэтому чем меньше букв в логическом выражении, тем меньше логических операций необходимо для реализации этого выражения, тем меньше логических элементов требуется для построения соответствующей комбинационной схемы. Это ведет к минимуму веса устройства, минимуму стоимости и т.д.

Как правило, все алгоритмы минимизации начинаются с приведения переключательной функции к канонической форме, в качестве которой используются совершенные дизъюнктивная и конъюнктивная нормальные формы. Основные этапы минимизации приведены на рис. 2.1.

Рис. 2.1. Основные этапы минимизации ПФ

Смысл минимизации переключательных функций заключается в поиске совокупности таких элементарных конъюнкций (дизъюнкций), которые своими единицами (нулями) накрывали бы как можно большее число единиц (нулей) среди значений заданной переключательной функции.

Понятие вхождения одной переключательной функции в другую является весьма существенным, поскольку именно оно во многом определяет "механизм" минимизации переключательных функций.

Будем говорить, что переключательная функция j(х₁, х₂, …, х_n) входит в переключательную функцию f(х₁, х₂, …, х_n), если функция j накрывает своими нулями все нули функции f, а единицы функции f накрываются как нулями, так и единицами функции j; т.е. функция j должна иметь нулевых значений не меньше, чем функция f, и, кроме того, нули функции j должны быть определенным образом расположены.

Определение 2.1. Функция j(х₁, х₂, …, х_n), входящая в функцию f(х₁, х₂, …, х_n), называется импликантой этой функции.

Применение термина "импликанта" связано с переключательной функ­цией двух переменных f₁₃(x,y) = x® y, именуемой импликацией. Восполь­зо­вав­шись таблицей истинности для функции f₁₃(x,y), можно убедиться в том, что выражение j®f тождественно равно единице, т.е. является всегда истинным только тогда, когда функция j входит в функцию f. Тот факт, что j входит в f обозначается следующим образом: j Ì f.

Рассмотрим таблицу истинности для некоторых функций двух переменных (табл. 2.1).

Таблица 2.1

x1
x2
f6(х1, х2) f4(х1, х2) f2(х1, х2) f0(х1, х2)
f3(х1, х2)

Очевидно, что f₄(x₁,x ₂) Ì f₆(x₁,x ₂); f₂(x₁,x ₂) Ì f₆(x₁,x ₂); f₀(x₁,x ₂) Ì f₆(x₁,x ₂), т.е. функции f₄, f₂, f₀ являются импликантами функции f₆. Кроме того, очевидно, что в соответствии с определением понятия вхождения функции в функцию f₆(x,y) Ì f₆(x,y). Если сравнить значения функций f₆(x,y) и f₃(x,y) на всех наборах аргументов, то можно заключить, что f₃(x,y)Ëf₆(x,y), т.е. функция f₃ в функцию f₆ не входит.

Определение 2.2. Функция j(х₁, х₂, …, х_n) называется простой им­пли­кантой функции f(х₁, х₂, …, х_n), если сама функция j входит в функ­цию f, но никакая собственная часть функции j в f не входит.

Если некоторая импликанта представлена, например, в виде элементарного логического произведения, то ее собственные части могут быть получены путем исключения из данного произведения одного или нескольких сомножителей. Например, произведение x₁×x₂×x₃ имеет такие собст­вен­ные части: x₁, x₂, x₃, x₁×x₂, x₁×x₃ и x₂×x₃.

Предположим, что выполняются следующие условия:

x₁×x₂×x₃ x₄Ì f(х₁, х₂, х₃, х₄),

x₁ ×x₃Ì f(х₁, х₂, х₃, х₄),

x₁ Ë f(х₁, х₂, х₃, х₄),

x₃ Ë f(х₁, х₂, х₃, х₄),

т.е. элементарное произведение x₁×x₃ является простой импликантой функции f(х₁, х₂, х₃, х₄). Символ Ë означает, что в данном случае условие вхождения одной функции в другую не выполняется.

Простые импликанты представляют собой самые короткие элементарные произведения, входящие в данную переключательную функцию. Очевидно, что если какое-либо элементарное произведение входит в данную переключательную функцию, то при добавлении к нему любых сомножителей новое произведение также всегда будет входить в эту функцию, так как оно обращается в нуль вместе с исходным произведением.

Теорема 2.1. Любая переключательная функция равняется дизъ­юнк­ции всех своих простых импликант.

Для доказательства рассмотрим наборы, на которых заданная переключательная функция равна нулю. Так как все простые импликанты входят в переключательную функцию по определению, то они будут также равны нулю на этих наборах, а следовательно, будут равны нулю и их дизъюнкции.

Рассмотрим далее наборы, на которых переключательная функция равна единице. Для каждого такого набора найдется хотя бы одна импликанта, равная на этом наборе единице. Действительно, простые импликанты выбираются среди всех элементарных произведений, входящих в переключательную функцию. В число этих произведений входят и все конституенты единицы данной функции. Но любая простая импликанта является собственной частью некоторых конституент единицы (или совпадает с одной из них). Например, при трех переменных элементарное произведение х₁х₂ будет собственной частью конституент х₁х₂х₃ и , а элементарное произведение х₂ – собственной частью конституент , , , х₁х₂х₃.

Если некоторые конституенты единицы не входят в набор всех простых импликант, то это означает, что они заменяются более короткими элементарными произведениями – простыми импликантами. Простая импликанта равняется единице на тех же наборах, на которых равны единице входящие в нее конституенты. Следовательно, среди всех простых импликант всегда найдутся такие, которые вместе с заданной функцией обращаются на данном наборе в единицу.

Таким образом, дизъюнкция всех простых импликант накрывает все нули и все единицы заданной функции и, следовательно, совпадает с этой функцией.

Теорема Квайна

Теорема 2.2. (теорема Квайна). Если в совершенной дизъ­юнк­тив­ной нормальной форме переклю­ча­тель­ной функции выполнить все опе­ра­ции неполного склеивания, а затем все операции поглощения, то в результате будет получена сокращенная дизъ­юнк­тивная нормальная фор­ма этой функции, или дизъюнкция всех ее простых импликант.

Следует обратить внимание на требование теоремы "выполнить все операции неполного склеивания" и "все операции поглощения". Кроме того, теорема дает определение сокращенной дизъюнктивной нормальной формы переключательной функции – это дизъюнкция всех ее простых импликант.

Точно так же теорема Квайна формулируется применительно к конъ­юнк­тив­ным формам переключательных функций.

Важность этой теоремы обусловлена тем, что она определяет конструк­тив­ное правило нахождения всех простых импликант переключательной функ­ции.

Доказать теорему можно путем следующих рассуждений. Прежде всего покажем, что в результате проведения операций непол­но­го склеивания получим все простые импликанты. Для этого рассмотрим операцию, обратную операции склеивания, называемую операцией раз­вер­ты­вания. Операция развертывания заключается в умножении некоторых импликант на выражение типа 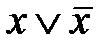= 1, что, естественно, не меняет их значений. С помощью операции развертывания любую простую импли­канту можно представить в виде дизъюнкции конституент единицы.

Пусть, например, 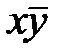– простая импликанта переключательной функции че­ты­рех аргументов: x, y, z, u. Тогда, применяя дважды операцию развер­тыва­ния, получаем

.

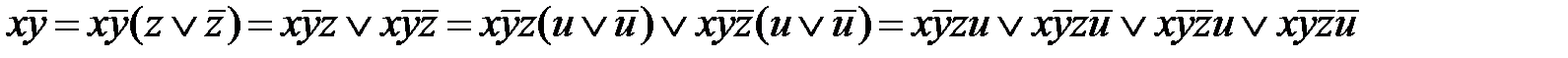Сокращенная дизъюнктивная нормальная форма содержит все простые им­пликанты заданной функции. Применяя к каждой импликанте операцию раз­вертывания, получаем, очевидно, все конституенты единицы этой функ­ции.

При развертывании различные импликанты могут, вообще говоря, образовать одну и ту же конституенту. Поэтому после проведения операций развертывания полученное выражение может содержать несколько одина­ко­вых конституент. Если дизъюнкцию одинаковых конституент заменить одной конституентой, то получим совершенную дизъ­юнк­тивную нормальную форму заданной переключательной функции.

Так как операция развертывания является обратной по отношению к операции склеи­ва­ния, то, применяя операции склеивания к совершенной дизъюнктивной нормальной форме, можно получить любую простую импликанту. Для того чтобы получить все простые импликанты, необходимо провести операции неполного склеивания. Это связано с тем, что одно и то же логическое слагаемое дизъюнктивной формы может склеиваться с несколькими другими, образуя при этом различные импликанты. Поэтому при проведении операций склеивания каждое логическое слагаемое следует оставлять в выражении для использования его при других склеиваниях.

Полученная после проведения всех операции неполного склеивания дизъюнктивная форма будет содержать кроме всех простых импликант и другие логические слагаемые (в том числе все конституенты единицы переключательной функции). Если теперь провести все операции поглощения, то в дизъюнктивной форме останутся только простые импликанты. Покажем это.

Пусть, например, после проведения всех операций склеивания дизъюнктивная форма будет содержать слагаемое q, не являющееся простой импликантой. Тогда оно должно входить в данную функцию (qÌf), так как в противном случае полученное выражение не равняется исходному. Но по предположению q не является простой импликантой и входит в функций f; следовательно, в эту функцию входит какая-то его часть p, которая будет простой импликантой. Тогда q = q1p и слагаемое q будет поглощаться простой импликантой p:

.

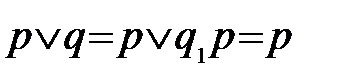Это и доказывает теорему Квайна.

Подчеркнем, что в соответствии с теоремой Квайна преобразование нужно начинать, исходя из совершенной дизъюнктивной нормальной формы.Поэтому если функция задана в произвольной форме, то ее следует преобразовать в совершенную дизъюнктивную нормальную форму и только затем проводить операции склеивания и поглощения. При задании функции в произвольной дизъюнктивной нормальной форме для получения совер­шен­ной формы достаточно применить операции развертывания.

Практически сокращенную дизъюнктивную нормальную форму удобно на­ходить в такой последовательности.

Провести в совершенной дизъюнктивной нормальной форме функции f(x1, x2, …, xn) все возможные операции склеивания конституент единицы. В результате этого образуются произведения, содержащие (n-1) букв. Заметим, что конституенты единицы в дальнейшем не будут склеиваться ни с одним вновь полученным логическим слагаемым, так как склеиваться могут только произведения с одинаковым количеством букв. Поэтому можно сразу же провести операции поглощения, а затем выполнить все возможные склеивания слагаемых, состоящих из (n-1) букв. После этого провести поглощения слагаемых с (n-1) буквой и вновь выполнить операции склеивания слагаемых с числом букв, равным (n-2), и т.д.

Метод импликантных матриц

Этот метод позволяет достаточно просто осуществлять переход от со­кра­­щенной формы переключательной функции к тупиковым и минимальным формам. Рассмотрим пример. Требуется найти минимальные дизъюнктивные нормальные формы переключательной функции, совершенная форма кото­рой определяется выражением

.

Построим для этой функции импликантную матрицу, представляющую собой таблицу, в вертикальные и горизонтальные входы которой записы­ваются все конституенты единицы и все простые импликанты заданной функции соответственно (табл. 2.2).

Таблица 2.2

Импликантная матрица

Простые импликанты	Конституенты единицы
	´	´
		´	´
			´	´
				´	´
					´	´

Для каждой импликанты найдем конституенты еди­ницы, которые ею поглощаются, т. е. те конституенты, собственной частью которых является данная импликанта. Например, импликанта поглощает конституен­ты и , импликанта — конституенты и и т. д. Клетки импликантной матрицы, образованные пересечением строк с импликантами и колонок с поглощаемыми ими конституентами, отметим какими-либо символами.

Чтобы получить минимальную дизъюнктивную нормальную форму заданной функции, достаточно найти минимальное число импликант, которые совместно накрывают крестиками все колонки импликантной матрицы.

Из табл. 2.2 следует, что в минимальную форму обя­зательно должны войти импликанты и , так как только они накрывают крестиками первую и шестую колонки импликантной матрицы.

Кроме того, импликанта накрывает вторую, а импликанта — пятую колонки. Поэтому остается накрыть только третью и четвертую колонки. Для этого можно выбрать пары импликант: и ; и или одну импликанту . Если выбрать указанные выше пары импликант, то импликанты и оказываются лишними, так как импликанта одна накрывает третью и четвертую колонки таблицы. Таким образом, выбрав импликанту , получим ми­нимальную дизъюнк­тивную нормальную форму задан­ной функции:

,

которая совпадает с первой тупиковой формой. Если дополнительно к и выбрать импликанты и , то лишних импликант не ока­зы­ва­ет­ся, а полученное выражение

является второй тупиковой формой заданной функ­ции.

Пример 2.1. Найти минимальные формы переключатель­ной функции:

. (2.1)

Проводя все операции неполного склеивания и поглощения, по­лучим сокра­щен­ную дизъюнктивную нормальную форму:

(2.2)

. (2.3)

Составим импликантную матрицу (табл. 2.3), выпи­сав из выражения (2.1) все конституенты единицы, а из выражения (2.3) - все простые импликанты. При заполнении импликантной матрицы удобно пользоваться формой записи (2.2): следует поставить крестики в тех колонках, номера которых совпадают с числами, стоящими в левой части формулы (2.2).

Таблица 2.3

Импликантная матрица

Простые импликанты	Конституенты единицы
	´	´
	´		´
		´				´
			´	´
				´	´
					´	´

Для импликанты крестиками отмечаются первая и вторая колон­ки; для — первая и третья и т. д. Заметим, что каж­дая колонка табл. 2.3 отмечена двумя крестиками. По­этому из выражения (2.3) можно исключить любую импликанту. Минимальное количество импликант, накрывающих крестиками все колонки, равно трем:

накрывает первую и вторую колонки,

накрывает третью и четвертую колонки,

накрывает пятую и шестую колонки.

Поэтому минимальная дизъюнктивная нормальная форма заданной функции имеет вид:

.

Можно накрыть все колонки табл. 2.3 и другими импликантами:

накрывает первую и третью колонки,

накрывает вторую и шестую колонки,

накрывает четвертую и пятую колонки.

Таким образом, данная функция имеет вторую минимальную форму:

.

Переключательная функция имеет не­сколько других тупико­вых форм, которые, однако, не являются минимальными. Например, тупико­выми будут следующие формы:

На основании изложенного сформулируем алгоритм получения мини­мальных дизъ­юнктивных нормальных форм переключательной функции.

1. Переключательную функцию представляют в совершенной дизъюнк­тив­ной нормальной форме. Если функция задана в произ­вольной ана­литической форме, то совершенную дизъ­юнктивную нормальную форму можно получить, при­меняя операции развертывания, правила де Моргана и другие формулы булевой алгебры.

2. В полученной совершенной дизъюнктивной нор­мальной форме про­во­дят все операции неполного склеивания и поглощения. В результате этого по­лу­чается сокращенная дизъюнктивная нор­мальная форма заданной функции.

3. Находят минимальные дизъюнктивные нор­мальные формы по импли­кантной матрице. Если коли­чество импликант в сокращенной дизъюнк­тив­ной нормаль­ной форме невелико, то можно найти тупиковые формы методом испытания импликант и выбрать среди них мини­мальные.

В ряде случаев минимальная дизъюнк­тивная форма совпа­да­ет с сокращенной. Например, сокращенная дизъюнктивная нормальная фор­ма любой переключательной функции двух аргументов совпадает с ми­ни­маль­ной формой.

Точно так же импликантные матрицы применяются для по­лу­чения ту­пи­ко­вых и минимальных конъюнктивных нормальных форм переключательных функций.

Метод испытания импликант

Этот метод удобно использовать тогда, когда число импликант, вхо­дя­щих в сокращенную форму функции, невелико.

Отметим следующее свойство произвольной, в частности, сокращенной дизъюнктивной нормальной формы переключательной функции:

¨ если из этой формы исключить одну или несколько импликант, то по­лу­ченное после этого выражение будет обращаться в нуль на тех же наборах, что и исходное выражение.

Это связано с тем, что дизъюнктивная форма обращается в нуль только в том случае, когда все ее логические слагаемые равны нулю. Однако при исключении импликанты может оказаться, что на тех наборах, на которых исключенная импликанта равнялась единице (а следовательно, вместе с ней и вся дизъюнкция равнялась единице ввиду соотношения 1Úх = 1), оставшееся вы­ражение не будет равно единице. Если же проверкой установить, что при исключении импликанты полученное выражение равно единице на этих наборах, то можно утверждать, что все нули и все единицы обоих выражений совпадают и, следовательно, исключенная импликанта является лишней.

Таким образом, чтобы испытать некоторую импликанту, ее следует исключить из сокращенной дизъюнктивной нормальной формы и подставить в оставшееся выражение такие значения переменных, которые обращают исключенную импликанту в единицу. Если при этом оставшееся выражение будет тождественно равно единице, то испытываемая импликанта является лишней.

Применение этого правила связано с некоторыми особенностями, кото­рые можно рассмотреть на примерах.

Пример 2.2. Найти тупиковые формы переключательной функции, задан­ной в сокращенной дизъюнктивной нормальной форме:

.

1. Испытываем импликанту . Подставляем в значения х₁ = 0 и х₂ = 0, т.к. при этом = :

.

Следовательно, импликанту исключать нельзя, т.к. оставшееся выраже­ние не равно тождественно единице.

2. Импликанту х₁х₃ исключать также нельзя, т.к. при х₁= 1 и х₃ = 1

.

3. Для импликанты

.

Полученное выражение тождественно равно единице, поэтому импли­кан­ту можно исключить, т.к. она является лишней.

Пример 2.3.Упростить переключательную функцию:

.

На основе теоремы Квайна получим

1 - 2 ®

2 - 3 ®

3 - 4 ®

4 - 5 ®

5 - 6 ®

Тогда сокращенная ДНФ имеет вид

. (2.4)

Найдем тупиковые формы.

1. Для : х₁ = 0, х₃ = 1, х₄ = 1:

,

т.е. первую импликанту исключать нельзя.

2. Для : х₂ = 0, х₃ = 1, х₄ = 1:

т.е. импликанта является лишней.

3. Проверяем третью импликанту ; при этом вторую импликанту, которая оказалась лишней, вновь возвращаем в исследуемое выражение. Тогда, подставляя в выражение

Ú Ú Ú

значения х₁ = 1, х₂ = 0, х₄ = 1, получим

.

Следовательно, импликанта также является лишней и может быть ис­ключена.

4. Аналогично можно показать, что и импликанта также может быть исключена.

Таким образом выражение (2.4) имеет три лишние импликанты: и .

Исключать одновременно все лишние импликанты без дополнительной проверки нельзя. Вначале следует исключить одну импликанту полученного выражения. Исключив из выражения (2.4.1) импликанту , получим

.

Вновь проверяем наличие лишних импликант, проверяя только те, которые были лишними при первой проверке, т.е. импликанты и .

Подставляя в выражение

Ú Ú

значения х₁ = 1, х₂ = 0, х₄ = 1, получаем

Следовательно, импликанту исключать нельзя, хотя при первой про­вер­ке, т.е. при наличии (тоже лишней) она была лишней.

Поэтому если в некотором выражении имеется несколько лишних имп­ли­кант, то исключение двух и более импликант одновременно без допол­ни­тельной проверки недопустимо.