Перечень компьютерных программ, наглядных и других пособий, методических указаний, материалов и технических средств обучения

ОБЩИЕ СВЕДЕНИЯ

Сведения об ЭУМК

Электронный учебно-методический комплекс по дисциплине «Дискретная математика и математическая логика» предназначен для студентов всех технических специальностей вузов, а также может быть использован преподавателями, аспирантами и практическими работниками предприятий.

Электронный учебно-методический комплекс составлен на основе рабочей учебной программы по курсу « Дискретная математика и математическая логика », утверждённой деканом факультета непрерывного и дистанционного обучения <дата утверждения>, регистрационный № УД 11‑XX‑YY/Р и рабочего учебного плана специальностей Н.08.02.00 «Информатика» и Т.12.01.00 «Телекоммуникационные системы».

Составители:

Э.А. Баканович, доцент кафедры информатики Учреждения образования «Белорусский государственный университет информатики и радиоэлектроники», кандидат технических наук.

Н.А. Волорова, доцент кафедры информатики Учреждения образования «Белорусский государственный университет информатики и радиоэлектроники», кандидат технических наук.

А.В. Епихин, ассистент кафедры информатики Учреждения образования «Белорусский государственный университет информатики и радиоэлектроники».

Рассмотрен и рекомендован к изданию на заседании кафедры информатики, протокол № 22 от 28.06.2010.

Одобрен и рекомендован к изданию методической комиссией факультета компьютерных систем и сетей, протокол № __ от __.__.2010.

Методические рекомендации по изучению дисциплины

Студенты дистанционной формы обучения специальности информатики в соответствии с учебным планом изучают дисциплины «Дискретная математика и математическая логика». Предусмотрено изучение основных разделов дискретной математики и математической логики, рассмотрение наиболее важных практических задач, возникающих при исследованиях дискретных моделей. Учебным планом предусмотрено выполнение двух контрольных работ.

Завершается изучение дисциплины «Дискретная математика и математическая логика» сдачей экзамена; следует иметь в виду, что к экзамену допускаются студенты, самостоятельно выполнившие и защитившие контрольные работы. Перечень экзаменационных вопросов находится здесь.

Курс имеет традиционную структуру, многократно опробованную в БГУИР и в других ВУЗах и полностью соответствующую структуре построения большинства учебников и учебных пособий по данной дисциплине. Поэтому для усвоения материала целесообразно придерживаться следующей последовательности изучения материала.

Сначала, целесообразно внимательно ознакомиться с содержанием курса по рабочей учебной программе, обращая особое внимание на логическую связь различных разделов. Затем следует изучить материал, имеющийся в ЭУМК и являющийся лишь основой изучаемой дисциплины. После этого целесообразно обратиться к литературным источникам, перечисленным в программе, обращая основное внимание на вопросы и разделы, приведенные в рабочей учебной программе курса. Усвоению материала может способствовать изучение одних и тех же разделов программы по различным учебникам и учебным пособиям. Следует обратить внимание на разделы дискретной математики и логики, указанные в рабочей учебной программе. Теоретическую часть курса целесообразно изучать, усвоив материал ЭУМК, а затем используя материал различных литературных источников. Параллельно следует обращаться к контрольным вопросам, пытаясь найти на них ответы в ЭУМК и в другой учебной литературе.

Особое внимание следует уделить решению задач и выполнению контрольных работ, учитывая возможность применения приобретенных навыков при изучении других дисциплин специальности Информатика.

Теоретический материал следует изучать в той последовательности, которая указана в рабочей программе.

Рабочая учебная программа

Учреждение образования

“Белорусский государственный университет информатики и радиоэлектроники”

Утверждаю

Декан факультета НДО

_________ Бондарик В.М.

“___”___________ 2010 г.

Регистрационный № УД- _______ /р.

Дискретная математика и математическая логика

Рабочая учебная программа для специальности 1-31 03 04

Информатика

Факультет непрерывного и дистанционного обучения

Кафедра информатики

Курс 2

Часть 1, 2

ИПР 2

Контрольных работ 2

Всего часов по дисциплине 245

В том числе:

Часть 1 - 90

Часть 2 - 155

Экзамен 4 семестр

Форма получения

высшего образования: дистанционная

Рабочая учебная программа составлена на основе учебной программы по дисциплине “Дискретная математика и математическая логика” для высших учебных заведений по специальности 1-31 03 04 “Информатика”, утвержденной Министерством образования Республики Беларусь 05.07.06 г. Регистрационный № ТД-G, 099/тип и учебного плана специальности

1-31 03 04 “Информатика”.

Составитель программы доцент кафедры информатики к.т.н. Баканович Э.А.

Рассмотрена и рекомендована к утверждению на заседании кафедры информатики, протокол

№ 22 от “ 29 ” 06 2009 г.

Заведующий кафедрой ___________ Минченко Л.И.

Одобрена и рекомендована к утверждению Советом факультета компьютерных систем и сетей Учреждения образования “Белорусский государственный университет информатики и радиоэлектроники”, протокол № ______ от “___” ____________ 2009 г.

Председатель ________________ Прытков В.А.

Согласовано

Начальник ОМОУП ____________ Шикова Ц.С.

Пояснительная записка

Основной спецификой курса ”Дискретная математика и математическая логика” (ДМ И МЛ) являются изучение алгоритмической основы и демонстрация эффективности использования дискретности в современной науке. Курс ДМ и МЛ включает ряд разделов, которые интенсивно стали развиваться в середине прошлого столетия в связи с появлением ЭВМ. Этот курс является не только фундаментом математической кибернетики, но и важным звеном математического образования специалистов в области прикладной математики и информатики.

Цель преподавания дисциплины

Целью преподавания дисциплины “Дискретная математика и математическая логика” является подготовка студентов по ряду разделов дискретной математики, широко используемых при синтезе специализированных цифровых структур, при создании и исследовании изделий электронной техники и сложных систем, при построении моделей каналов связи и средств телекоммуникаций, при создании систем автоматизации научных исследований, испытаний и моделирования различных структурно сложных объектов, при разработке алгоритмов и оценке их эффективности, при проектировании информационных процессов в системах и исследовании их характеристик.

Основные задачи, которые ставятся при изучении дисциплины

В результате изучения курса “Дискретная математика и математическая логика” студенты должны:

Знать

- основы теории переключательных функций и методы синтеза комбинационных схем, основы теории множеств и отношений, теорию графов и элементы комбинаторики, основные положения математической логики, области и методы ее применения.

Уметь

- применять на практике методы минимизации переключательных функций и синтеза комбинационных схем в различных базисах, пользоваться аппаратом теории графов при их матричной и теоретико-множественной интерпретации, применять аппарат производящих функций для анализа комбинаторных моделей.

Приобрести навыки

- использования основных разделов дискретной математики при решении задач в соответствии с профилем специальности.

Перечень дисциплин, усвоение которых необходимо для изучения данной дисциплины

№ пп	Название дисциплины	Раздел, тема
1.	Высшая математика	Общие понятия множества, функции, оператора, функционала. Векторный анализ. Матрицы.

Содержание дисциплины

1. Название тем лекционных занятий, их содержание, объем в часах.

№ пп	Название темы	Содержание	Объем в часах
Третий семестр
	Элементы теории переключательных функций. Синтез комбинационных схем
1.1	Переключательные функции и их свойства	Введение: содержание курса ДМ и МЛ и его роль в подготовке инженера-системотехника. Определение переключательных функций; основные свойства. Набор значений аргументов. Способы задания переключательных функций: таблицы истинности, номер функции, логическое выражение.
1.2	Переключательные функции одной и двух переменных	Функции одной переменной. Таблица функций двух переменных. Функции тривиальные и нетривиальные. Конъюнкция, дизъюнкция, инверсия; функции Шеффера и Пирса, импликация, равнозначность. Связи между функциями двух переменных.
1.3	Теорема о функциональной полноте	Пять классов переключательных функций. Операции суперпозиции и подстановки переменных. Основная функционально полная система логических связей (ОФПС). Базис Жегалкина, теорема Жегалкина. Функции Шеффера и Пирса. Связи между различными базисами.

1.4	Законы алгебры логики в ОФПС	Коммутативный, ассоциативный, дистрибутивный законы. Правила Де-Моргана. Следствия из законов алгебры логики: операции склеивания, поглощения, правила развертывания логических выражений. Конституенты; совершенные дизъюнктивная и конъюнктивная нормальные формы.
1.5	Минимизация переключательных функций	Вхождение функции в функцию. Импликанты. Теорема Квайна-Мак-Класски. Сокращенные, тупиковые, минимальные формы. Критерий минимальности логического выражения.
1.6	Основные методы минимизации	Метод импликантных матриц. Метод диаграмм Вейча. Метод испытания импликант. Методы получения минимальных конъюнктивных нормальных форм.
1.7	Минимизация неполностью определенных переключательных функций	Постановка задачи минимизации. Эквивалентные переключательные функции. Теорема о минимальных дизъюнктивной и конъюнктивной нормальных формах неполностью определенной функции. Алгоритмы минимизации.
	Элементы теории графов
2.1	Основные понятия и определения теории графов	Определение понятия “граф”. Теоретико-множественная и геометрическая интерпретация графов. Компоненты графов: вершины, ребра, дуги, петли. Степени и полустепени вершин. Подграф. Орграф. Смежность, инцидентность. Графы плоские и планарные. Основные типы графов.
2.2	Теорема Понтрягина-Куратовского	Теорема о реализуемости графов в трехмерном пространстве. Графы К5 и К3,3. Понятие гомеоморфизма. Условие планарности графов.

2.3	Способы задания графов	Матрицы графов. Матрицы смежностей и инциденций графов и ор-графов. Сопряженные графы.
2.4	Операции на графах	Объединение и пересечение графов. Декартово произведение, произведение, композиция. Свойства операций на графах. Реализация операций в матричной и геометрической формах.
2.5	Связность графов	Понятие связности. Компоненты связности. Цепь, цикл, маршрут. Теоремы о связных графах. Эйлеровы и гамильтоновы графы. Условия существования эйлеровых цепей и циклов.
2.6	Графы-деревья	Определения дерева, леса. Свойства деревьев. Теорема А. Кэли. Каркас графа, условие существования каркаса. Алгоритм поиска минимального каркаса.
2.7	Потоки в транспортной сети	Определения транспортной сети, потока в транспортной сети. Понятие разреза и его свойства. Теорема Форда-Фалкерсона, алгоритм поиска максимального потока. Основные алгоритмы на графах.
Итого за третий семестр
Всего за учебный год

2. Перечень тем индивидуальных практических занятий, их наименование и объем в часах.

№ п.п.	Название темы	Содержание	Объем в часах
Третий семестр
1.	Переключательные функции и их свойства	Способы задания переключательных функций. Построение таблиц истинности по номеру функции. Совершенные дизъюнктивная и конъюнктивная нормальные формы. (СДНФ и СКНФ). Представление переключательных функций в виде полинома Жегалкина. Доказательство функциональной полноты. Базисы.
2.	Минимизация переключательных функций	Вхождение функции в функцию. Импликанты. Применение теоремы Квайна-Мак-Класски. Сокращенная форма переключательной функции. Получение тупиковых и минимальных форм. Метод импликантных матриц, диаграмм Вейча, испытания импликант.
3.	Матричное представление графов	Построение матриц смежностей и инциденций. Реберные (сопряженные) графы. Проверка связности графов.
4.	Операции на графах	Операции объединения и пересечения. Операции декартова произведения, произведения, композиции. Выполнение операций в матричной и геометрической формах.
Итого за третий семестр

ЛИТЕРАТУРА

Основная

4.1.1. Закревский А.Д., Поттосин Ю.В., Черемисинова Л.Д., Логические основы проектирования дискретных устройств. – М.: ФИЗМАТЛИТ , 2007,- 592 с.

4.1.2. Джеймс А. Андерсон. Дискретная математика и комбинаторика: Пер. с англ.- М.: Издательский дом “Вильямс”, 2003 г. – 960 с.

4.1.3. Белоусов А.И., Ткачев С.Б. Дискретная математика: Учебник для ВУЗов / Под ред. В.С. Зарубина, А.П. Крищенко. – М.: изд-во МГТУ им. Н.Э. Баумана, 2001 , -744 с. (Сер. Математика в техническом университете ; Вып. XIX).

4.1.4. Горбатов В.А. Фундаментальные основы дискретной математики. Информационная математика. – М.: Наука, ФИЗМАТЛИТ, 2000. – 544 с. – ISBN 5-02-015238-2.

4.1.5. Петрова В.Т. Лекции по алгебре и геометрии. Учебник для ВУЗов : в 2 ч. – М.: Гуманит. изд. Центр ВЛАДОС . – ч. 1 -312 с. ISBN 5-691-00077-2. ISBN 5-691-00238-4 (I), ISBN 5-691-00239-2(II). 1999.

4.1.6. Ерусалимский Я.М. Дискретная математика: теория, задачи, приложения. 3-е издание. – М.: Вузовская книга, 2000. – 280 с. ISBN 5-89522-034-7.

4.1.7. Яблонский С.В. Введение в дискретную математику. – М.: Изд-во “Наука”. – 1979. – 278 с.

4.1.8. Нефедов В.Н., Осипова В.А. Курс дискретной математики: Учебн. Пособие. – М.: Изд-во МАИ, 1992. 264 с.: ил. ISBN 5-703500157-X.

4.1.9. Сигорский В.П. Математический аппарат инженера. Издание 2-е, стереотипное. Изд-во “Техника” , Киев, 1977. – 768 с.

4.1.10. Коршунов Ю.М. Математические основы кибернетики. Издание второе, переработанное и дополненное. М.: Изд-во “Энергия”. – 1980. -385 с.

4.1.11. Вавилов Е.Н., Портной Г.П. Синтез схем электронных цифровых машин. – М.: Изд-во “Сов. радио”, 1963. -440 с.

4.1.12. Поспелов Д.А. Логические методы анализа и синтеза схем. Издание второе, переработанное и дополненное.- М.: Изд-во “Энергия”. – 1968.-340 с.

4.1.13. Емеличев В.А., Мельников О.И., Сарванов В.И., Тышкевич Р.И. Лекции по теории графов. – М.: Наука. Гл. Ред. Физ. – мат.лит., 1990.-384 с. – ISBN 5-02-013992-0

4.1.14. Фудзисава Т., Касами Т. Математика для радиоинженеров. Теория дискретных структур: пер. с япон. – М.: Радио и связь, 1984. -240 с., ил.

4.1.15. Кузнецов О.П., Адельсон-Вельский Г.М. Дискретная математика для инженера. 2-е издание, переработанное и дополненное. – М.: Энергоатомиздат, 1988. – 480 с.: ил. ISBN 2-283-01563-7.

4.1.16. Баканович Э.А., Волорова Н.А., Епихин А.В. Дискретная математика: Учеб. Пособие для студентов специальностей Н.08.02.00 и Т.12.01.00. В 2-х ч. Ч1: Элементы теории графов и сетевые модели. – Мн.: БГУИР, 1998.- 80 с. ISBN 985-4440012-5 (ч.1).

4.1.17. Баканович Э.А., Волорова Н.А., Епихин А.В. Дискретная математика: Учеб. Пособие для студентов специальностей Н.08.02.00 и Т.12.01.00. В 2-х ч. Ч.2: Элементы теории переключательных функций.- Мн.: БГУИР, 2000. – 52 с. Ил.14. ISBN 985-444-057-5(ч.2).

4.1.18. Зарубин В.С. Математическое моделирование в технике: Учеб. Для ВУЗов / Под ред. В.С. Зарубина, А.П. Крищенко. – М.:Изд-во МГТУ им. Н.Э.Баумана, 2001. – 496 с. (Сер. Математика в техническом университете; вып.XXI, заключительный).

4.1.19. Бусленко Н.П. Моделирование сложных систем. М.: “Наука”,1968 г.

4.1.20. Ковалев М.М. Дискретная оптимизация. Изд-во БГУ, Минск, 1977 г.

4.1.21. Фомичев В.М. Дискретная математика и криптология. Курс лекций/Под ред.Н.Д. Подуфалова. – М.: ДИАЛОГ – МИФИ, 2003.

4.1.22. Закревский А.Д., Поттосин Ю.В., Черемисинова Л.Д. Основы логического проектирования в 3 кн. Кн. 1. Комбинаторные алгоритмы дискретной математики. – Мн.: ОИПИ НАН Беларуси. 2004.-226 с.

4.1.23. Закревский А.Д., Поттосин Ю.В., Черемисинова Л.Д. Основы логического проектирования в 3 кн. Кн. 2. Оптимизация в булевом пространстве. – Мн.: ОИПИ НАН Беларуси, 2004. – 240с.

4.1.24. Закревский А.Д., Поттосин Ю.В., Черемисинова Л.Д. Основы логического проектирования в 3 кн. Кн. 3. Проектирование устройств логического управления. – Мн.: ОИПИ НАН Беларуси, 2006. – 254 с.

Дополнительная

4.2.1. Закревский А.Д. Логический синтез каскадных схем. М.: Наука, 1981. – 414с.

4.2.2. Глушков В.М. Синтез цифровых автоматов. М.:ГИФМЛ, 1962. – 476с.

4.2.3. Миллер Р. Теория переключательных схем, Т.1. – М.: Наука, 1970. - 416с.

4.2.4. Миллер Р. Теория переключательных схем, Т.2. – М.: Наука, 1971. – 304с.

4.2.5. Гилл А. Введение в теорию конечных автоматов. – М.: Наука, 1966. – 272с.

4.2.6. Ангер С. Асинхронные последовательностные схемы. – М.: Наука, 1977. – 400с.

4.2.7. Кристофидес Н. Теория графов. Алгоритмический подход. – М.: Мир, 1978. – 432с.

4.2.8. Баранов С.И. Синтез микропрограммных автоматов. – Л.: Энергия, 1979. – 232с.

4.2.9. Скляров В.А. Синтез автоматов на матричных БИС. – Минск: Наука и техника,1984. – 287с.

4.2.10. Лазарев В.Г., Пийль Е.И. Синтез управляющих автоматов. – М.: Энергоатомиздат, 1989. -328с.

4.2.11. Савельев А.Я. Прикладная теория цифровых автоматов. – М.: Высшая школа, 1987. – 272с.

4.2.12. Глушков В.М., Капитонова Ю.В., Мищеко А.Т. Логическое проектирование дискретных устройств. – Киев: Наукова думка, 1987. – 264с.

4.2.13. Фридман А., Менон П. Теория и проектирование переключательных схем. – М.: Мир, 1978. – 580с.

4.2.14. Теория прикладного кодирования: Учебное пособие. В 2т./В.К. Конопелько, В.А. Липницкий и др.; под ред. проф. В.К. Конопелько. – Мн.: БГУИР, 2004.

4.2.15. Лидл П., Нидеррайтер Г. Конечные поля: В 2т. – М.: Мир, 1988.

4.2.16. Горбатов В.А. Основы дискретной математики. Учеб. Пособие для студентов ВУЗов. – М.: Высш.шк., 1986. – 311с.

4.2.17. Судоплатов С.В., Овчинникова Е.В. Элементы дискретной математики: Учебник. – М.:ИНФА-М, НОВОСИБИРСК : Изд-во НГТУ, 2002. – 280с. – (Серия “Высшее образование”).

4.2.18.Татт У. Теория графов : пер. с англ. М.: Мир, 1988. – 424с. Ил. ISBN 5-03-001001-7.

ПО ИЗУЧАЕМОЙ УЧЕБНОЙ ДИСЦИПЛИНЕ

С ДРУГИМИ ДИСЦИПЛИНАМИ СПЕЦИАЛЬНОСТИ

(дисциплины, изучение которых опирается на данную дисциплину)

Название дисциплины, с которой требуется согласование	Кафедра, обеспечивающая изучение этой дисциплины	Предложения об изменениях в содержании учебной программы по изучаемой дисциплине	Решение, принятое кафедрой, разработавшей учебную программу (с указанием даты и номера протокола)[1]
1. Теория вероятностей и математическая статистика	Информатики	Нет
2. Имитационное и статистическое моделирование	Информатики	Нет
3. Архитектура вычислительных систем	Информатики	Нет

Зав. кафедрой информатики Минченко Л.И.

ТЕОРЕТИЧЕСКИЙ РАЗДЕЛ

Лекции

ПЕРЕКЛЮЧАТЕЛЬНЫЕ ФУНКЦИИ

1.1 Основные понятия и определения

Будем рассматривать только функции конечного числа аргументов.

Рассмотрим множество векторов 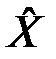={<x₁, … , x_n>}, координаты которых могут принимать лишь два значения - 0 или 1. Тогда множество 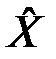состоит из 2ⁿ различных векторов. Сопоставим каждому вектору из 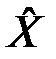символы 0 или 1, т.е. произведем однозначное отображение множества X на множество Y = {0,1}.

Определение 1.1.1. Функцией алгебры логики, или переключательной функцией, называется функция, дающая однозначное отображение 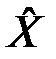в Y [1].

Из этого определения следует, что функция f(x_{1, … ,}x_n) называется переключательной, если она, так же как и ее аргументы, может принимать только значения из двухбуквенного алфавита, например, 0 и 1.

Поскольку аргументы переключательной функции могут принимать только два значения, то область определения любой переключательной функции конечна. Совокупность значений аргументов называется набором и обозначается a₁, …, a_i, …, a_n, где a_i равно 0 или 1 (i = 1, …, n). Каждый набор может быть представлен n–разрядным двоичным числом, а количество двоичных n–разрядных чисел равно 2ⁿ. Поэтому любая переключательная функция может быть определена на 2ⁿ наборах.

Например, переключательные функции двух аргументов определены на четырех наборах (00, 01, 10, 11), а переключательные функции трех аргументов – на восьми. Таким образом, переключательная функция может быть задана таблицей, в которой перечислены все возможные значения аргументов функции (наборы) и соответствующие этим наборам значения функции. Такая таблица называется таблицей истинности переключательной функции. Пример переключательной функции трех аргументов приведен в табл. 1.1.

Таблица 1.1

Таблица значений переключательной функции

x1
x2
x3
f(x1,x2,x3)

Каждому набору аргументов можно приписать номер, равный двоичному числу, соответствующему данному набору:

0,0,0,0,0 — нулевой набор;

0,0,0,0,1 — первый набор;

. . . . . . . . . . . . . . . . . . . . . . .

1,1,1,1,1 — тридцать первый набор.

Набор, содержащий все единицы (1,1, …, 1), называют единичным набором.

Переключательная функция n аргументов определена на 2ⁿ наборах, на которых она может принимать значения 0 или 1. Поэтому в соответствие каждой переключательной функции можно поставить 2ⁿ-разрядное двоичное число. Количество 2ⁿ-разрядных двоичных чисел равно 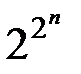. Таким образом, число различных переключательных функций n аргументов конечно и равно .

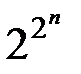Припишем каждой переключательной функции номер, равный двоичному числу, образованному значениями переключательной функции на всех наборах. Этот номер записывается слева направо, начиная со значения функции на нулевом наборе. Например, двоичное число, образованное значениями функции из табл. 1.1, 00111010₍₂₎, равно 58 в десятичной системе счисления и функцию можно обозначить следующим образом:

f(x₁,x₂,x₃) = f₅₈(x₁,x₂,x₃).

Пример 1.1. Составить таблицу истинности для переключательной функции номер 23805 четырех аргументов.

Решение. Переключательная функция четырех аргументов определяется на 2⁴ = 16 наборах (табл. 1.2) . Для получения значений функций представим число 23805 в двоичной системе счисления: 23805₍₁₀₎ =

= 101110011111101₍₂₎. Полученное двоичное число имеет 15 двоичных разрядов, и для представления переключательной функции необходимо дополнить полученный код до 16-разрядного: 0101110011111101.

Таблица 1.2

Таблица переключательной функции f₂₃₈₀₅(x₁,x₂,x₃,x₄)

x1

x2

x3

x4

f23805(x1,x2,x3,x4)

Определение 1.1.2. Если две переключательные функции f(x₁, …, x_n) и φ(x₁, …, x_n) одного и того же числа аргументов принимают на всех возможных наборах значений аргументов одинаковые значения, то функции f и φ называются равными.

Факт равенства функций f и φ записывается так:

f(x₁, …, x_n) = φ(x₁, …, x_n).

Определение 1.1.3. Переключательная функция f(x₁, …x_i-1,x_i,x_i+1, …, x_n) существенно зависит от аргумента x_i, если имеет место соотношение

f(x₁, …x_i-1, 0, x_i+1, …, x_n) ¹f(x₁, …x_i-1, 1, x_i+1, …, x_n).

В противном случае говорят, что от аргумента x_i функция зависит несущественно и x_i является ее фиктивным аргументом. Переключательная функция не изменится, если к ее аргументам дописать любое число фиктивных аргументов или зачеркнуть те аргументы, которые являются фиктивными.

Конституенты.

В п. 1.2 был рассмотрен один из возможных способов представления переключательной функции – задание ее в виде таблицы истинности. В этом разделе будем решать обратную задачу, а именно представление переключательной функции, заданной таблицей истинности, через элементарные функции, образующие базис.

Рассмотрим переключательные функции, называемые конституентами.

Определение 1.3.1. Конституентой единицы называют переключательную функцию n аргументов, которая принимает значение, равное единице на одном единственном наборе аргументов.

Из определения следует, что число различных конституент единицы среди функций n аргументов равно 2ⁿ. Конституенты единицы обозначаются так: K_i(x₁, …, x_n), где i – номер набора, на котором конституента равна единице. Например, запись K₇(x₁, x₂, x₃, x₄) означает функцию четырех аргументов, равную единице на наборе (0111).

Конституента единицы может быть выражена через конъюнкцию всех аргументов, каждый из которых входит в произведение со знаком отрицания или без него. Приведенную выше конституенту единицы можно представить через конъюнкцию аргументов следующим образом:

K₇(x₁, x₂, x₃, x₄) = .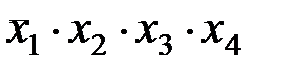

Чтобы записать в виде произведения конституенту K_i(x₁, …, x_n), можно воспользоваться следующим правилом: записать n-разрядное двоичное число (n – число аргументов), равное i, и конъюнкцию n переменных; над переменными, места которых совпадают с позициями нулей в двоичном числе i, поставить знак отрицания.

Пример 3.1. Записать конституенту, равную единице на двенадцатом наборе для функции пяти переменных.

Решение. Пятиразрядное двоичное число, равное двенадцати, записывается в виде: 01100. Запишем произведение пяти аргументов, располагая их в порядке возрастания индексов: x₁×x₂×x₃×x₄×x₅. Сопоставляя это произведение с двоичным числом 01100, определяем, что знаки отрицания необходимо поставить над первым, четвертым и пятым аргументами:

K₁₂(x₁, x₂, x₃, x₄, x₅) = .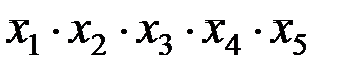

Определение 1.3.2. Конституентой нуля называют переключательную функцию n аргументов, которая принимает значение, равное нулю, на одном единственном наборе аргументов.

Из определения следует, что число различных конституент нуля среди функций n аргументов равно 2ⁿ. Конституенты нуля обозначаются так: M_i(x₁, …, x_n), где i – номер набора, на котором конституента равна нулю. Конституента нуля может быть выражена через дизъюнкцию всех аргументов, каждый из которых входит в произведение со знаком отрицания или без него.

Чтобы записать в виде произведения конституенту M_i(x₁, …, x_n), можно воспользоваться следующим правилом: записать n-разрядное двоичное число (n – число аргументов), равное i, и дизъюнкцию n переменных; над переменными, места которых совпадают с позициями единиц в двоичном числе i, поставить знак отрицания.

Пример 3.2. Записать конституенту нуля, равную нулю на двадцать пятом наборе для функции пяти переменных.

Решение. Пятиразрядное двоичное число, равное двадцати пяти, записывается в виде: 11001. Запишем дизъюнкцию пяти аргументов, располагая их в порядке возрастания индексов: x₁Úx₂Úx₃Úx₄Úx₅. Сопоставляя это произведение с двоичным числом 11001, определяем, что знаки отрицания необходимо поставить над первым, вторым и пятым аргументами:

M₂₅(x₁, x₂, x₃, x₄, x₅) = .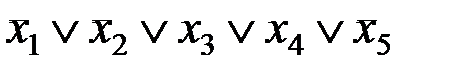

Теорема Квайна

Теорема 2.2. (теорема Квайна). Если в совершенной дизъ­юнк­тив­ной нормальной форме переклю­ча­тель­ной функции выполнить все опе­ра­ции неполного склеивания, а затем все операции поглощения, то в результате будет получена сокращенная дизъ­юнк­тивная нормальная фор­ма этой функции, или дизъюнкция всех ее простых импликант.

Следует обратить внимание на требование теоремы "выполнить все операции неполного склеивания" и "все операции поглощения". Кроме того, теорема дает определение сокращенной дизъюнктивной нормальной формы переключательной функции – это дизъюнкция всех ее простых импликант.

Точно так же теорема Квайна формулируется применительно к конъ­юнк­тив­ным формам переключательных функций.

Важность этой теоремы обусловлена тем, что она определяет конструк­тив­ное правило нахождения всех простых импликант переключательной функ­ции.

Доказать теорему можно путем следующих рассуждений. Прежде всего покажем, что в результате проведения операций непол­но­го склеивания получим все простые импликанты. Для этого рассмотрим операцию, обратную операции склеивания, называемую операцией раз­вер­ты­вания. Операция развертывания заключается в умножении некоторых импликант на выражение типа 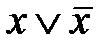= 1, что, естественно, не меняет их значений. С помощью операции развертывания любую простую импли­канту можно представить в виде дизъюнкции конституент единицы.

Пусть, например, 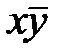– простая импликанта переключательной функции че­ты­рех аргументов: x, y, z, u. Тогда, применяя дважды операцию развер­тыва­ния, получаем

.

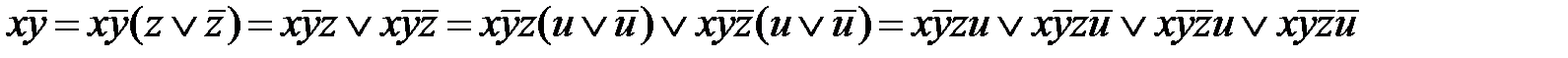Сокращенная дизъюнктивная нормальная форма содержит все простые им­пликанты заданной функции. Применяя к каждой импликанте операцию раз­вертывания, получаем, очевидно, все конституенты единицы этой функ­ции.

При развертывании различные импликанты могут, вообще говоря, образовать одну и ту же конституенту. Поэтому после проведения операций развертывания полученное выражение может содержать несколько одина­ко­вых конституент. Если дизъюнкцию одинаковых конституент заменить одной конституентой, то получим совершенную дизъ­юнк­тивную нормальную форму заданной переключательной функции.

Так как операция развертывания является обратной по отношению к операции склеи­ва­ния, то, применяя операции склеивания к совершенной дизъюнктивной нормальной форме, можно получить любую простую импликанту. Для того чтобы получить все простые импликанты, необходимо провести операции неполного склеивания. Это связано с тем, что одно и то же логическое слагаемое дизъюнктивной формы может склеиваться с несколькими другими, образуя при этом различные импликанты. Поэтому при проведении операций склеивания каждое логическое слагаемое следует оставлять в выражении для использования его при других склеиваниях.

Полученная после проведения всех операции неполного склеивания дизъюнктивная форма будет содержать кроме всех простых импликант и другие логические слагаемые (в том числе все конституенты единицы переключательной функции). Если теперь провести все операции поглощения, то в дизъюнктивной форме останутся только простые импликанты. Покажем это.

Пусть, например, после проведения всех операций склеивания дизъюнктивная форма будет содержать слагаемое q, не являющееся простой импликантой. Тогда оно должно входить в данную функцию (qÌf), так как в противном случае полученное выражение не равняется исходному. Но по предположению q не является простой импликантой и входит в функций f; следовательно, в эту функцию входит какая-то его часть p, которая будет простой импликантой. Тогда q = q1p и слагаемое q будет поглощаться простой импликантой p:

.

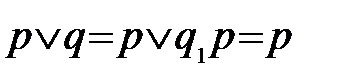Это и доказывает теорему Квайна.

Подчеркнем, что в соответствии с теоремой Квайна преобразование нужно начинать, исходя из совершенной дизъюнктивной нормальной формы.Поэтому если функция задана в произвольной форме, то ее следует преобразовать в совершенную дизъюнктивную нормальную форму и только затем проводить операции склеивания и поглощения. При задании функции в произвольной дизъюнктивной нормальной форме для получения совер­шен­ной формы достаточно применить операции развертывания.

Практически сокращенную дизъюнктивную нормальную форму удобно на­ходить в такой последовательности.

Провести в совершенной дизъюнктивной нормальной форме функции f(x1, x2, …, xn) все возможные операции склеивания конституент единицы. В результате этого образуются произведения, содержащие (n-1) букв. Заметим, что конституенты единицы в дальнейшем не будут склеиваться ни с одним вновь полученным логическим слагаемым, так как склеиваться могут только произведения с одинаковым количеством букв. Поэтому можно сразу же провести операции поглощения, а затем выполнить все возможные склеивания слагаемых, состоящих из (n-1) букв. После этого провести поглощения слагаемых с (n-1) буквой и вновь выполнить операции склеивания слагаемых с числом букв, равным (n-2), и т.д.

Метод импликантных матриц

Этот метод позволяет достаточно просто осуществлять переход от со­кра­­щен