Передача теплоты через многослойную плоскую стенку и граничных условиях I рода.

Передача теплоты через плоскую однослойную и многослойную стенки и граничных условиях III рода.

1.2.2 Краткое содержание вопросов:

Передача теплоты через плоскую стенку и граничных

Условиях I рода

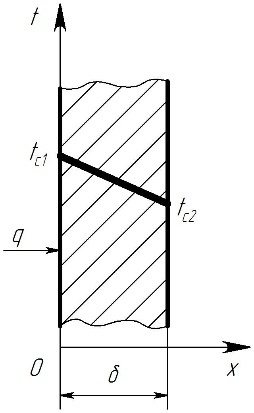Рассмотрим однородную и изотропную стенку толщиной d с постоянным коэффициентом теплопроводности l. На наружных поверхностях стенки поддерживаются постоянными температуры tc1 и tc2. Следовательно, температура будет изменяться только в направлении оси Ох, а температура в направлении осей Oy и Oz будет оставаться постоянной:

.

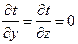В связи с этим температура будет функцией только одной координаты х (t = f(x)) и дифференциальное уравнение теплопроводности запишется в виде:

.

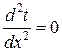Граничные условия в рассматриваемой задаче задаются следующим образом:

t = t_c1 при х = 0;

t = t_c2 при х = d.

В результате решения поставленной задачи найдем распределение температуры в плоской стенке, то есть t = f(x), а также получим формулу для определения плотности теплового потока.

Первое интегрирование дает:

.

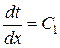После второго интегрирования получим:

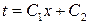– уравнение прямой линии.

Следовательно, при l = const закон изменения температуры при прохождении теплоты через плоскую стенку будет линейным.

Постоянные интегрирования С₁ и С₂ определяем из граничных условий:

при х = 0 t = t_c1 Þ С₂ = t_c1;

при х = d t = t_c2 .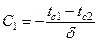

Тогда закон распределения температуры в рассматриваемой плоской стенке имеет следующую запись:

.

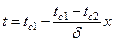Для определения плотности теплового потока в направлении оси Ох, воспользуемся законом Фурье, согласно которому:

.

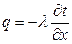Так как 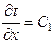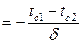, то

.

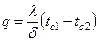Из полученного уравнения следует, что количество теплоты, проходящее через единицу поверхности в единицу времени, прямо пропорционально коэффициенту теплопроводности l, разности температур поверхностей стенки и обратно пропорционально толщине стенки d.

Величина, численно равная отношению разности температур между двумя изотермическими поверхностями тела к плотности теплового потока в какой-либо точке на одной из этих поверхностей, называется внутренним термическим сопротивлением, м²×К/Вт:

.

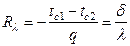Общее количество теплоты Q_t, которое передается через поверхность стенки F за промежуток времени t:

.

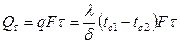
Кроме того, уравнение температурного поля может быть записано в виде:

.

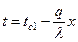Из этого выражения следует, что при прочих равных условиях температура в стенке убывает тем быстрее, чем больше плотность теплового потока.

Полученные выражения справедливы, когда l = const.

В действительности l является переменной величиной. Для многих материалов зависимость коэффициента теплопроводности от температуры близка к линейной:

,

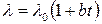
где l₀ – значение коэффициента теплопроводности при 0 °С.

Тогда плотность теплового потока будет равна:

.

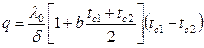
Введя обозначение 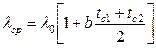, получим

,

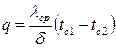
где l_ср – среднеинтегральное значение коэффициента теплопроводности.

Выражение для температурного поля имеет вид:

.
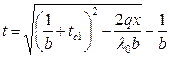