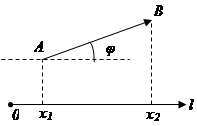Линейные операции над векторами. Линейное пространство
I. Сложение векторов
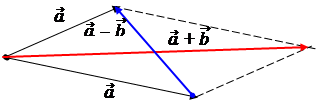
Правило треугольника
def.Суммой векторов  и
и  называется вектор
называется вектор  =
=  +
+  , который соединяет начало 1-го вектора с концом 2-го, при условии, что точка приложения 2-го вектора находится в конце 1-го. Распространяется на любое конечное число векторов.
, который соединяет начало 1-го вектора с концом 2-го, при условии, что точка приложения 2-го вектора находится в конце 1-го. Распространяется на любое конечное число векторов.
 |
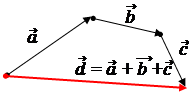
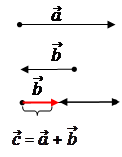
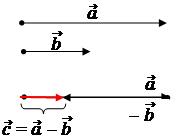
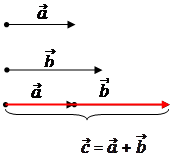 Частный случай. Сложение коллинеарных векторов.
Частный случай. Сложение коллинеарных векторов.
|
Правило параллелограмма
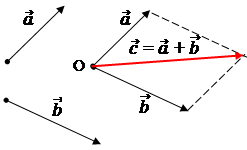
Отложить от т. О векторы  и
и  . Построить на этих векторах как на сторонах параллелограмм. Вектор, служащий диагональю параллелограмма, проведенный из т. О, является суммой
. Построить на этих векторах как на сторонах параллелограмм. Вектор, служащий диагональю параллелограмма, проведенный из т. О, является суммой  +
+  .
.
II. Вычитание векторов
def. Разностью двух векторов  и
и  называется вектор
называется вектор  =
=  -
-  , который при сложенным с вектором
, который при сложенным с вектором  дает вектор
дает вектор  .
.
Если  =
=  -
-  , то
, то  +
+  =
=  .
.
Из определения вытекает правило построения  -
-  .
.
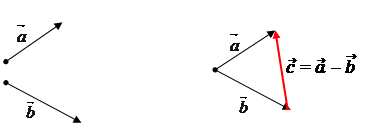 |
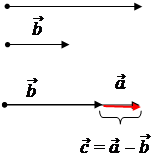
Вектор  =
=  -
-  направлен из конца вычитаемого к концу уменьшаемого.
направлен из конца вычитаемого к концу уменьшаемого.
|
 |
 Итак:
Итак:
III. Умножение вектора на число
def. Произведением вектора  на число λ называется вектор λ
на число λ называется вектор λ  :
:
1) коллинеарный вектору  ;
;
2) имеющий длину 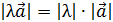 ;
;
3)  тоже направление, что и
тоже направление, что и  , если
, если 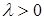 , противоположное направлению
, противоположное направлению  , если
, если 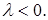
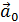 - единичный вектор (орт) вектора
- единичный вектор (орт) вектора  , т.е.
, т.е. 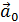 коллинеарен
коллинеарен  , одинакового с ним направления,
, одинакового с ним направления, 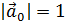 . Тогда
. Тогда
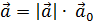 или
или 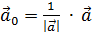 .
.
Операции сложения векторов и умножения вектора на число называются линейными. Они обладают следующими свойствами:
1) ("  ,
,  )
)  +
+  =
=  +
+  (коммутативность сложения);
(коммутативность сложения);
2) ("  ,
,  ,
, 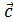 ) (
) (  +
+  ) +
) +  =
=  + (
+ (  +
+  ) (ассоциативность сложения);
) (ассоциативность сложения);
3) ("  )
)  +
+ 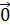 =
=  ;
;
4) ("  )
)  + (
+ ( 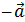 ) =
) = 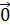 ;
;
5) ("  , " a, b Î R) a (b
, " a, b Î R) a (b  ) = (a b)
) = (a b)  ;
;
6) ("  ) 1×
) 1×  =
=  ;
;
7) ("  , " a, b Î R) (a + b)
, " a, b Î R) (a + b)  = a
= a  +b
+b  ;
;
8) ("  ,
,  , " a Î R) a (
, " a Î R) a (  +
+  ) = a
) = a  + a
+ a  .
.
Множество векторов пространства (плоскости), удовлетворяющих свойствам 1–8, образуют линейное (векторное) пространство, которое обозначается R3 (R2).
Замечание. Операции сложения векторов и умножения вектора на число можно распространить на множество объектов произвольной природы. Тогда получим обобщенное понятие линейного (векторного) пространства.
def. Множество 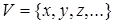 называется линейным (векторным) пространством, если: 1)
называется линейным (векторным) пространством, если: 1) 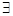 правило, которое
правило, которое 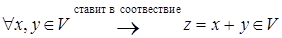 ;
;
2) 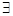 правило, которое
правило, которое 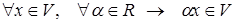 .
.
При этом сумма 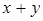 и произведение
и произведение 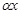 удовлетворяет свойствам 1–8.
удовлетворяет свойствам 1–8.
Проекция вектора на ось
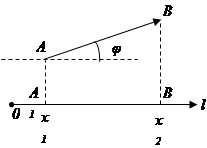 Пусть даны: l – некоторая ось и
Пусть даны: l – некоторая ось и 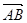 – произвольный вектор.
– произвольный вектор.
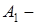 проекция А на ось l,
проекция А на ось l, 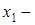 координата
координата 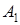 на l;
на l;
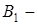 проекция B на ось l,
проекция B на ось l, 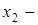 координата
координата 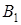 на l.
на l.
def. Проекцией вектора 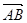 на ось называется разность
на ось называется разность 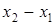
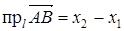 .
.
Обозначим 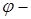 угол между
угол между 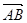 и l;
и l; 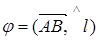 – наименьший угол, на который надо повернуть единичный вектор
– наименьший угол, на который надо повернуть единичный вектор 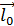 оси l до совпадения с
оси l до совпадения с 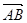 .
.
|  острый угол острый угол  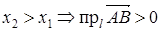 | |||
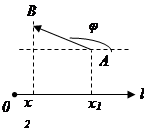 | 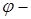 тупой угол тупой угол 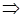 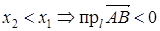 | |||
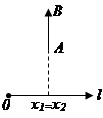 | 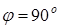  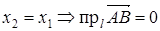 |
Свойства проекций
1. Проекция вектора 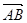 на ось l равна модулю вектора
на ось l равна модулю вектора 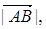 умноженному на косинус угла
умноженному на косинус угла 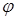 между
между 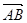 и осью l.
и осью l.
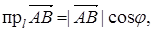 где
где 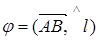 .
.
Доказательство.
1 случай. 
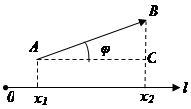
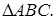
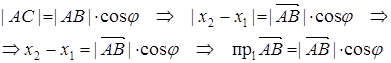
2 случай. 
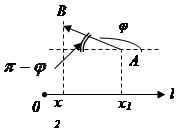
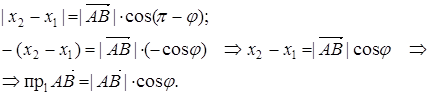
Свойство доказано.
2. Проекция суммы векторов на ось равна сумме проекций слагаемых векторов на
ту же ось.
 Доказательство.
Доказательство.
3. При умножении вектора на число проекция на ось также умножается на это число.
l ×  Þ прl (l
Þ прl (l  ) = l прl
) = l прl  .
.
Доказательство.
1 случай. 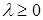 . прl (l
. прl (l  ) =
) = 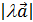 cos j = l
cos j = l 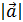 cos j = l прl
cos j = l прl  .
.
2 случай. 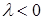 . прl (l
. прl (l  ) =
) = 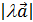 cos (p - j ) = - l
cos (p - j ) = - l 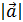 (- cos j) = l прl
(- cos j) = l прl  .
.
4. Проекции двух равных векторов на одну и ту же ось равны.
 =
=  Þ прl
Þ прl  = прl
= прl  .
.