Лекция №10. Динамическое описание систем
Функционирование сложной системы можно представить как совокупность двух функций времени: x(t) - внутреннее состояние системы; y(t) - выходной процесс системы. Обе функции зависят от u(t) - входного воздействия и от f(t) - возмущения.
Для каждого t Î T существует множество z ÎZ.
Z=Z1 ´ Z2 ... ´ Zn - множество n мерного пространства. Состояние системы z(t) - точка или вектор пространства Z с обобщенными координатами z1, z2, z3, z4, ....., zn.
U=T ´ Z - фазовое пространство системы.
Детерминированная система без последствий
Детерминированная система без последствий - система состояние которой z(t) зависит только от z(t0) и не зависит от z(0) ... z(t0), т.е. z(t) зависит от z(t0) и не зависит от того каким способом система попала в состояние z(t0).
Для систем без последствия еее состояние можно описать как:
z(t)= H{t,t0,z(t0), (t, xL]t0t},
где {(t, xL]t0t} - множество всевозможных отрывков входных сообщений, соответствующих интервалу (t0, t]. H - оператор переходов системы.
tÎT, t0ÎT, z(t0) ÎZ, (t, xL]t0tÎ {(t, xL]t0t}.
Формальная запись отображения:
T ´ T ´ {(t, xL]t0t} ® Z.
Начальные условия H{t0, t0, z(t0), (t, xL]t0t0 } = z(t0).
Если (t, xL1]t0t = (t, xL2]t0t, то H{t0, t, z(t0), (t, xL1]t0t } = H{t0, t, z(t0), (t, xL2]t0t}
Если t0<t1<t2 и t0, t1, t2 Î T, то H{t0, t2, z(t0), (t, xL]t0t2 } = H{t2, t1, z(t1), (t, xL2]t1t2}, так как (t, xL]t0t2 есть сочленение отрезков (t, xL]t0t1 и (t, xL]t1t2.
Оператор выходов системы G реализует отношение
{(t, t0)} ´ Z ´ (t, xL)T} ® Y,
y(t) = G(t, t0, z(t0), (t, xL2]t0t).
(x, y) Î X ´ Y - расширенное состояние системы.
Динамическая система без последствий (динамическая система Кламана) -упорядоченное множество (T, X, Z, Y, {(t, xL)T, H, G), удовлетворяющие поставленным выше требованиям:
1. T является подмножеством действительных чисел.
2. {(t, xL)T}- множество отображений T®X, удовлетворяющие сочленению отрезков.
3. Оператор переходов H реализует {(t, t0)} ´ Z ´ (t, xL)T} ® Y.
4. Оператор выходов системы G задается видом y(t) = G(t, t0, z(t0), (t, xL2]t0t).
Детерминированные системы без последствия с входными сигналами двух классов
Расширение понятие системы идет по трем путям:
1. учет специфики воздействий;
2. учет последствий;
3. учет случайных факторов.
Учет специфики воздействий
Вводится понятие управляющих сигналов u Î U; u=M(t), или если сигнал u Î U описывается набором характеристик. U = U1 ´ U2 ´ UL.
Отличие от предыдущего случая, то что множество моментов времени tu и tx могут не совпадать.
Вводится расширенное множество X*= X ´ U, таким образом состояние системы описывается вектором x = (x, u) = (x1, x2, .... , xn, u1, u2, .... , uL).
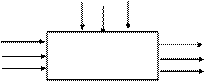 |
Рис.
С учетом этого предыдущие формулы приобретают вид.
оператор переходов:
z(t)= H{t,t0,z(t0), (t, xL, uM]t0t}, или
z(t)= H{t,t0,z(t0), (t, xL]t0t, (t, uM]t0t }, что соответствует отображению
T ´ T ´ {(t, xL]T}´ {(t, uM]T} ® Z.
Детерминированные системы с последствием
Большой класс систем характеризуется тем, что для представления их состояния необходимо знать состояние системы на некотором множестве моментов времени.
z(t)= H{t,(tB0, zw)t0, (t, xL]t0t, (t, uM]t0t },
{(t, t0)} ´ {(tB0, zw)t0} ´ Z ´ {(t, xL]T} ® Z.
Где {(tB0, zw)t0} - семейство всевозможных состояний системы.
Стохастические системы
Системы функционирующие под воздействием случайных факторов, называются стохастическими. Для их описания вводится случайный оператор:
w Î W - пространство элементарных событий с вероятностной мерой P(A).
Случайный оператор H1, переводящий множество X в множество Z:
z = H1(x, w), реализующий отображение множества W в множество {X®Z }
Оператор переходов будет представлен соответственно:
z(t)= H1{t,t0,z(t0, w0), (t, xL]t0t, w`},
y(t) = G1(t, z(t), w`` ).
Где w0, w’, w’’ - выбираются из W в соответствии с P0(A), Px(A), Py(A).
При фиксированных w’, w’’ - система со случайными начальными состояниями.
При фиксированных w0, w’’ - система со случайными переходами.
При фиксированных w0, w’ - система со случайными выходами.
Агрегатное описание систем
Агрегат - унифицированная схема, получаемая наложением дополнительных ограничений на множества состояний, сигналов и сообщений и на операторы перехода а так же выходов.
t Î T - моменты времени; x Î X - входные сигналы; u Î U - управляющие сигналы; y Î Y - выходные сигналы; z Î Z - состояния, x(t), u(t), y(t), z(t) - функции времени.
Агрегат - объект определенный множествами T, X, U, Y, Z и операторами H и G реализующими функции z(t) и y(t). Структура операторов H и G является определяющей для понятия агрегата.
Вводится пространство параметров агрегата b=(b1, b2, ...,bn) Î B.
Оператор выходов G реализуется как совокупность операторов G` и G``. Оператор G` выбирает очередные моменты выдачи выходных сигналов, а оператор G`` - содержание сигналов.
у=G``{t, z(t),u(t),b}.
В общем случае оператор G`` является случайным оператором, т.е. t, z(t), u(t) и b ставится в соответствие множество y с функцией распределения G``. Оператор G` определяет момент выдачи следующего выходного сигнала.
Операторы переходов агрегата. Рассмотрим состояние агрегата z(t) и z(t+0).
Оператор V реализуется в моменты времени tn , поступления в агрегат сигналов xn(t). Оператор V1 описывает изменение состояний агрегата между моментами поступления сигналов.
z(t’n + 0) = V{ t’n, z(t’n), x(t’n), b}.
z(t) = V1(t, tn, z(t+0),b}.
Особенность описания некоторых реальных систем приводит к так называемым агрегатам с обрывающимся процессом функционирования. Для этих агрегатов характерно наличие переменной соответствующий времени оставшемуся до прекращения функционирования агрегата.
Все процессы функционирования реальных сложных систем по существу носят случайный характер, по этому в моменты поступления входных сигналов происходит регенерация случайного процесса. То есть развитие процессов в таких системах после поступления входных сигналов не зависит от предыстории.
Автономный агрегат - агрегат который не может воспринимать входных и управляющих сигналов.
Неавтономный агрегат - общий случай.
Частные случаи агрегата:
Кусочно-марковский агрегат - агрегат процессы в котором являются обрывающими марковскими процессами. Любой агрегат можно свести к марковскому.
Кусочно-непрерывный агрегат - в промежутках между подачей сигналов функционирует как автономный агрегат.
Кусочно-линейный агрегат. dzv(t)/dt = F(v)(zv).
Представление реальных систем в виде агрегатов неоднозначно, в следствие неоднозначности выбора фазовых переменных.
Иерархические системы
Иерархический принцип построения модели как одно из определений структурной сложности. Иерархический и составной характер построения системы.
Вертикальная соподчиняемость.
Право вмешательства. Обязательность действий вышестоящих подсистем.
Страты - уровни описания или абстрагирования. Система представляется комплексом моделей - технологические, информационные и т.п. со своими наборами переменных.
Слои - уровни сложности принимаемого решения:
1. срочное решение;
2. неопределенность или неоднозначность выбора.
Разбитие сложной проблемы на более простые: слой выбора способа действия, слой адаптации, слой самоорганизации.
Многоэшелонные системы. Состоит из четко выраженных подсистем, некоторые из них являются принимающими решения иерархия подсистем и принятия решений.
Декомпозиция на подсистемы - функционально-целевой принцип, декомпозиция по принципу сильных связей.
